MA. Integrais de superfície de segundo tipo
Mínimo teóricoEste tópico dá continuidade à discussão sobre integrais curvilíneas e de superfície que começou no tópico "". É recomendável que você se familiarize com este tópico com antecedência. Devido à maior complexidade do tema, integrais curvilíneas e de superfície
o segundo tipo é considerado separadamente. Integrais de superfície do segundo tipo são discutidas aqui - talvez a operação integral mais complexa em
análise de funções de muitas variáveis. O plano será completamente semelhante à consideração de uma integral curvilínea de segundo tipo. Vamos começar com aplicações físicas,
e então passaremos para o aspecto matemático formal.1. Aplicações físicas da integral de superfície de segundo tipo
A maneira mais natural de introduzir uma integral de superfície do segundo tipo é considerar o fluxo de um fluido através de alguma superfície. Vamos começar com um caso simples:
o líquido flui ao longo do eixo x com velocidade constante. Vamos selecionar uma área perpendicular ao fluxo e encontrar a massa de fluido que passa por ela.
ela a tempo. Durante este tempo, foi criado um “paralelepípedo” com altura e área de base de. A massa deste “paralelepípedo”
igual a, onde está a densidade do líquido.
Agora deixe o líquido fluir paralelo ao plano em um ângulo com o eixo x, mas ainda com velocidade. O site do anterior
caso ainda o colocaremos perpendicularmente ao eixo das abcissas. Com o tempo, um “paralelepípedo” inclinado passa por ele (ver Fig. 1). Sua massa
igual a . Observe que a introdução de um vetor normal unitário no site nos permite escrever.
É introduzido um vetor formal de uma área elementar, cujo módulo é igual a , e sua direção coincide com a direção do vetor
normal no local. Então. Esta notação permite que você não se preocupe com a direção do vetor velocidade do fluido em relação a
para o site.Resta abandonar a pequenez da área através da qual o líquido flui e a suposição de um módulo e direção de velocidade constantes. Então
a superfície é dividida em pequenas partes, dentro das quais o vetor velocidade pode ser considerado constante. A massa de líquido que passa pela superfície é
é aproximadamente dado pela soma.
A fórmula exata será obtida no limite da divisão da superfície em partes infinitesimais. O limite é uma integral de superfície do segundo tipo:.
Na redação desta seção, foi utilizado um fragmento de material didático de um professor do Departamento de Física Geral, utilizado por ele em aulas de seminário.2. Definição de uma integral de superfície de segundo tipo
Agora, sobre a construção formal da integral. Devido ao fato do campo vetorial estar integrado sobre a superfície, faz sentido esclarecer de que lado
superfície, a integral é calculada (como no cálculo do fluxo de um líquido: o líquido flui para a superfície ou sai dela). Portanto, é especialmente especificado
que a superfície sobre a qual a integração é realizada deve ser bilateral ou orientável (ou seja, a tira de Möbius como um todo não funcionará). Superfície
imediatamente orientado, ou seja, uma certa direção da normal à superfície é selecionada (por exemplo, se a integral for calculada sobre uma esfera, então a normal pode ser
direcionado da esfera ou para dentro da esfera). Os componentes do campo são, no caso geral, funções de um ponto. Superfície de integração
é dividido em pequenas partes, um ponto é selecionado em cada parte e a soma é compilada
,
onde é a área de projeção do elemento no plano, é a área de projeção deste elemento no plano, é a área
projeção deste elemento em um plano. Realizamos a soma de todos os elementos em que a superfície está dividida:
e vá até o limite, direcionando o diâmetro da maior região parcial para zero. O limite é uma integral de superfície do segundo tipo
.
Vamos mostrar como reduzir esta integral à forma do passo 1. Para isso, será necessário fazer uma pequena digressão de natureza puramente geométrica. Deixe estar
plano que cruza os eixos coordenados (ver Fig. 2). A parte deste plano localizada no primeiro octante possui área de . Você precisa encontrar a área
todas as três projeções ortogonais de uma determinada parte do plano em planos coordenados. Como se sabe, a área de projeção de uma figura é igual ao produto da área
a própria figura e o cosseno do ângulo entre o plano da figura e o plano no qual ela é projetada (ver Fig. 3). Aqueles. preciso encontrar os ângulos que formam
plano com planos coordenados. O ângulo entre dois planos é igual ao ângulo entre suas normais. A unidade normal ao plano tem componentes,
quais são seus cossenos de direção. Portanto, o ângulo entre o plano e o plano é igual (ver Fig. 2) e, portanto, .
A mesma relação será válida para áreas infinitesimais: . E da mesma forma.
Levando em conta essas relações, a integral assume a forma
.
Aliás, essa forma de gravação é mais visual, então vamos trabalhar com ela.Inverter a direção da normal faz com que a integral mude de sinal.
3. Cálculo da integral de superfície de segundo tipo
Depois de reduzir a integral a uma forma contendo as direções cossenos da normal à superfície, o problema se reduz essencialmente a escrever a normal unitária
com cálculo adicional da integral de superfície do primeiro tipo. Existem algumas especificidades nessas ações, então vamos analisar o cálculo em detalhes
integrais deste tipo.Vamos começar com o caso em que a superfície de integração é dada por uma equação explícita, por exemplo,
. Então o vetor normal é escrito da seguinte forma:
,
e o elemento de área de superfície.
Como resultado, a integral de superfície assume a seguinte forma:
, (1)
onde é a região do plano na qual a superfície de integração é projetada.Pode ser que a superfície de integração esteja corretamente projetada no plano (e dada pela equação) ou no plano
(e é dado pela equação). Em seguida, a fórmula pela qual a integral é calculada é ligeiramente ajustada:
(2)
ou
. (3)
Claro que não é recomendável memorizar tais fórmulas: é fácil confundir alguma coisa - é melhor restaurá-las em relação a um determinado
cálculo novamente, com base na fórmula do vetor normal e da área de um pequeno elemento de superfície.Há um caso destacado em que a superfície é projetada corretamente em todos os três planos de coordenadas, ou seja, da equação de superfície qualquer variável
pode ser expresso de forma inequívoca. Então o cálculo é significativamente simplificado. Preste atenção à estrutura das fórmulas (1) - (3). Em cada um deles há três
termos, e um deles parece mais simples que os outros. Ao projetar uma superfície em um plano, este termo contém o componente
Campos ; quando projetado em um plano, este é o termo que contém o componente; quando projetado em um plano, este é o termo
contendo componente. Se a superfície se projetar corretamente em qualquer plano coordenado, então dividimos a integral
em três partes e projete cada parte da maneira mais conveniente:
.Finalmente, o caso de definir parametricamente a superfície
.
Assim como no cálculo de uma integral de superfície do primeiro tipo, três Jacobianos precisam ser considerados:
.
Os cossenos de direção da normal são expressos através deles:
,
elemento de superfície
.
Assim, para a integral obtemos
,
onde está a faixa de alterações de parâmetros correspondentes à superfície de integração.4. Fórmula de Stokes. Fórmula de Ostrogradsky-Gauss
A integral de superfície do segundo tipo está associada a duas fórmulas que encontram diversas aplicações, inclusive em aplicações físicas.
Fórmula de Stokes:
,
Onde ,
a superfície é esticada ao longo do contorno, o percurso do contorno é consistente com a escolha da normal à superfície de acordo com a regra do parafuso da direita.
Esclarecimentos são necessários se a superfície de integração tiver “buracos”.
A fórmula de Green é um caso especial desta fórmula. Além disso, da fórmula de Stokes segue a condição para a independência da integral curvilínea do segundo
mais ou menos pela forma do caminho.Fórmula de Ostrogradsky-Gauss.
Para um campo vetoriala fórmula está cumprida
onde a superfície limita o volume.A fórmula de Ostrogradsky-Gauss tem diferentes aplicações. Vejamos dois deles. Primeiro, é fácil provar que o volume de um corpo pode ser calculado
de acordo com a fórmulaEm segundo lugar, por vezes é necessário calcular uma integral de superfície do segundo tipo sobre uma superfície aberta, o que envolve cálculos complicados.
Em seguida, a superfície é fechada, a integral é convertida em tripla e a integral sobre a superfície adicionada é subtraída (veja o exemplo abaixo).Observação. As fórmulas de Stokes e Ostrogradsky-Gauss são escritas mais convenientemente na análise vetorial usando a rotação e a divergência do campo vetorial.
Exemplos de cálculo de integrais de superfície de segundo tipo
Exemplo 1. Integral plano.. Então obtemos) partes de um parabolóide elíptico (normal externo).
Vamos reescrever a integral na forma
.
A superfície de integração - um parabolóide elíptico - é projetada corretamente apenas no plano, então escrevemos a equação da superfície na forma
.
Encontre o vetor normal unitário:.
O conceito de integral dupla sobre uma região plana pode ser facilmente generalizado para o caso de integração sobre uma superfície. Seja (S) uma superfície (fechada ou aberta) e uma função contínua de um ponto nesta superfície. Divida (S) em partes
e deixe as áreas dessas partes e quaisquer pontos localizados nessas partes. Compilando a soma dos produtos
O limite desta soma com um aumento infinito no número de divisões e uma diminuição infinita em cada uma das partes é chamado de integral da função sobre a superfície
Suponhamos que retas paralelas ao eixo Z cruzam a superfície em apenas um ponto (Fig. 48) e deixem a projeção (S) estar no plano XOY. Utilizando a fórmula (26), que estabelece a ligação entre a área superficial elementar (S) e a área correspondente de sua projeção, podemos reduzir a integral sobre a superfície (S) à integral sobre a área plana:
neste caso, assume-se que é diferente de zero e que o valor da função no ponto N da região coincide com o valor da função especificada na superfície naquele ponto M, cuja projeção coincide com . Se a equação da superfície (S) for dada na forma explícita (22) e a função for expressa em termos de coordenadas, então, ao integrá-la, basta substituir a função na expressão. O denominador do lado direito de (29) é determinado pela terceira das fórmulas (24).
Observe que as integrais de superfície obviamente têm todas as propriedades de uma integral dupla indicada em, em particular, o teorema do valor médio vale para elas.
Vamos agora provar uma das principais fórmulas da teoria das integrais múltiplas - a fórmula de Ostrogradsky, que estabelece uma conexão entre a integral tripla sobre um volume e a integral sobre a superfície (S) que limita esse volume. Consideraremos como e onde as linhas retas paralelas ao eixo Z se cruzam (S) em não mais que dois
pontos. Vamos manter a mesma notação da Fig. 40. Vamos também levar em consideração a direção da normal a (S), e assumiremos que ela está direcionada para fora do volume (V) (normal externa) (Fig. 50). Esta direção forma um ângulo agudo com o eixo OZ na parte superior da superfície (I) e um ângulo obtuso na parte inferior (I). Portanto, na parte inferior notamos que na linha de contato da superfície (5) com o cilindro saliente (Fig. 50). A fórmula (26) dá
Seja, junto com a derivada, contínuo na região até (S). Consideremos a integral tripla da função. Usando a fórmula (16), teremos
Mas a integral da derivada é igual à diferença entre os valores da função antiderivada nos limites superior e inferior:
Substituindo por conforme as fórmulas (30), reduzimos a integração à integração sobre (S), e na primeira integral, contendo a ordenada variável da parte (I) da superfície (S), teremos que utilizar a primeira das fórmulas (30), e obtemos a integral sobre (II ), na segunda integral que contém você terá que usar a segunda das fórmulas (30), e obtém a integral sobre (I):
Os símbolos de z não podem mais ser escritos, pois é indicado em qual parte da superfície a integração está sendo realizada. No lado direito está a soma das integrais sobre as partes (II) e (I), ou seja, a integral sobre todo o
superfícies (S):
Se são funções que possuem as propriedades da função R, então, levando em consideração que
Com base em (31), podemos escrever a fórmula de integração por partes:
Exatamente da mesma maneira, tomando duas outras funções, poderíamos provar
Somando as três fórmulas obtidas termo a termo, chegamos à fórmula de Ostrogradsky
Da mesma forma que (31), são escritas fórmulas de integração por partes para derivadas em relação a x e y.
Por uma questão de brevidade, não escrevemos aqui os argumentos x, y, z das funções P, Q, mas devemos lembrar que estas são funções definidas em volume e contínuas com suas derivadas.
No próximo capítulo daremos um grande número de exemplos de aplicação da fórmula de Ostrogradsky.
Quantidades são funções definidas na superfície (S). Nós os consideramos contínuos. Pode-se fazer uma suposição mais geral, nomeadamente, assumir que (S) é dividido em um número finito de partes, em cada uma das quais as funções indicadas são contínuas. Este será o caso, por exemplo, se (S) for um poliedro.
Ao derivar a fórmula (31), assumimos que as linhas retas paralelas ao eixo cruzam a superfície (S) da região em não mais do que dois pontos. Não é difícil generalizar esta fórmula para áreas de forma mais geral. Notemos em primeiro lugar que se a superfície (S), além da parte superior (II) e da parte inferior (I), tem uma parte lateral cilíndrica com geratrizes paralelas ao eixo, então nesta parte lateral e adicionando esta parte à direita da fórmula (31) não altera o valor da integral de superfície, portanto toda a prova da fórmula permanece válida. Num caso mais geral, basta utilizar superfícies cilíndricas com geratrizes paralelas ao eixo para dividir num número finito de partes que satisfaçam as condições anteriores, e aplicar a fórmula (31) a cada parte. Somando as fórmulas assim obtidas, teremos no lado esquerdo uma integral tripla sobre todo o volume. No lado direito teremos a soma das integrais de todas as superfícies daquelas partes em que dividimos (v). As integrais sobre as superfícies cilíndricas auxiliares reduzidas, conforme indicado acima, são iguais a zero. Assim, como resultado da adição do lado direito, teremos uma integral sobre a superfície (S) do volume original. Assim, a fórmula (31) acaba sendo válida para domínios de forma mais geral.
Consideremos integrais de funções definidas em superfícies, as chamadas integrais de superfície.A teoria das integrais de superfície é em muitos aspectos semelhante à teoria das integrais curvilíneas. Existem integrais de superfície do primeiro e
do segundo tipo.
4.1. Integrais de superfície do primeiro tipo. Deixe a função f (x, y, z)
definido em uma superfície lisa por partes S, delimitada por um contorno suave por partes (Fig. 4.1). Vamos decompô-lo
respectivamente ∆ s 1, ∆ s 2..., ∆ s n. Tomando um ponto arbitrário M i (x i, y i, z i) dentro de cada parte S i, i = 1, n, calculamos o valor da função nele e fazemos a seguinte soma:
σ n= ∑ f (x eu, y eu, z eu) ∆ s eu | |||||
eu = 1 | para a função f (x, y, z) por |
||||
que é chamado integral | |||||
superfície S. | |||||
O limite final I deste | enquanto se esforça | ||||
o maior λ dos diâmetros de todas as superfícies parciais S i | |||||
1, n |
|||||
se existe e não depende nem do método de divisão da superfície em parciais, nem da escolha dos pontos, então é denominado integral de superfície do primeiro tipo (sobre a área de superfície) da função
f (x, y, z) ao longo da superfície S e é denotado pelo símbolo | ∫∫ f(x, y, z) ds. |
|
Então, por definição | ||
= ∫∫ f(x, y, z) ds. | ||
Eu = lim ∑ f(xi, yi, zi) ∆ si | ||
λ → 0i = 1 | ||
A integral de superfície do primeiro tipo é uma generalização da integral dupla, portanto as condições para a existência da integral dupla e suas propriedades são facilmente transferidas para a integral de superfície do primeiro tipo.
Cálculo de integrais de superfície do primeiro tipo reduz-se ao cálculo de integrais duplas: com base na equação de superfície S,
o integrando é transformado em duas variáveis, cujo intervalo será a projeção da superfície S no plano coordenado correspondente a essas variáveis.
Deixe a superfície S ser definida pela equação z = z (x, y) e z (x, y) ser contínua junto com suas derivadas parciais z ′ x, z ′ y em um domínio fechado S xy, que é a projeção de a superfície S no plano coordenado xOy, então
∫∫ f(x, y, z) ds= ∫∫ f(x, y, z(x, y)) 1 + (z′ x ) 2 + (z′ y ) dxdy. | ||
Sexy | ||
Esta fórmula expressa a integral de superfície do primeiro tipo através da integral dupla sobre a projeção da superfície S no plano coordenado xOy.
Integrais de superfície do primeiro tipo sobre a superfície S são calculadas de maneira semelhante através de integrais duplas sobre suas projeções sobre
planos coordenados xOz e yOz respectivamente: | |||
∫∫ f (x ,y ,z )ds = ∫∫ f (x ,y (x ,z ),z ) | 1+ (y ′ x )2 + (y ′ z )dxdz , | ||
Sxz | |||
∫∫ f (x, y,z)ds= ∫∫ f (x(y,z), y,z) | 1 + (x′ y )2 + (x′ z )dydz. | ||
S yz | |||
Usando integrais de superfície do primeiro tipo, é possível calcular a área superficial, bem como massa, momentos estáticos, momentos de inércia e coordenadas do centro de massa para superfícies de materiais com densidade de distribuição de massa superficial conhecida.
Exemplo 4.1. Calcular
∫∫ 1 + 4 x 2 + 4 y 2 ds , onde S faz parte do parábola-
loid de revolução z = 1 − x 2 − y 2 , cortado pelo plano z = 0 .
Solução. Vamos projetar a superfície
S para o plano xOy .
A projeção S xy é um círculo limitado pelo círculo x 2 + y 2 = 1 (Fig.
4.2). Calcularemos a integral de superfície dada usando a fórmula (4.2), para a qual encontramos z ′ x = − 2 x , z ′ y = − 2 y . Então, comprometendo-se em dobro
integrante | para o polar | coordenadas, | S xy é um círculo, |
||||||||
1 +4 x 2 +4 e 2 ds =∫∫ | 1+ 4x 2 + 4y 2 | 1 + 4 x2 + 4 y2 dxdy= |
|||||||||
Sexy | |||||||||||
= ∫∫ (1 +4 x 2 +4 y 2 ) dxdy = | |||||||||||
Sexy | |||||||||||
= ∫ d ϕ ∫ (1 +4 ρ 2 ) ρ d ρ =∫ | +ρ4) | dϕ= | ∫dϕ . |
||||||||
4.2. Superfícies de dupla face. A superfície S é chamada
bilateral, se percorrer qualquer contorno fechado situado na superfície S e não cruzar seus limites, ao retornar ao ponto inicial, não altera a direção da normal à superfície. Caso contrário, a superfície é chamada unilateral. Exemplos de superfícies bilaterais: plano, esfera e qualquer superfície definida pela equação z = z (x, y), onde z = z (x, y), z ′ x (x, y), z ′ y (x , y) - contínuo em alguma áreaG. Um exemplo de superfície unilateral é uma tira de Möbius.
4.3. Integral de superfície do segundo tipo. Deixe S - superfície lisa dada pela equação z = z(x, y) e função f(x, y, z)
definido em pontos da superfície S.
Vamos selecionar um dos lados da superfície, ou seja, uma das duas direções possíveis da normal nos pontos da superfície (é assim que orientamos a superfície). Se as normais formam ângulos agudos com
Eixo de onça , então falaremos sobre o lado superior da superfície (sobre a direção positiva da normal ), e se as normais forem –ângulos obtusos com o eixo Oz, então estamos falando do lado inferior da superfície (a direção negativa da normal).
Vamos dividir a superfície S arbitrariamente em n partes S 1, S 2 ..., S n, e através (S xy ) eu denotamos a projeção da i-ésima parte da superfície
para o plano xOy. Dentro de cada superfície parcial S i , i = 1, n, escolha um ponto arbitrário M i (x i , y i , z i ) e calcule o valor da função
nele faremos a soma
σ n= ∑ f (x i, y i, z i) ∆ s i, i = 1
onde ∆ s i - área(S xy) i, tomado com sinal de mais se o lado superior da superfície S for selecionado e com sinal de menos se o lado inferior for selecionado
superfície S. Esta somaσ n é chamada soma integral para a função f(x, y, z).
O limite final I da soma integral, como o maior λ de todos os diâmetros de projeção (S xy ) i tende a zero, se existir e
não depende nem do método de partição da superfície S nem da escolha dos pontos
M i (x i, y i, z i), então este limite é chamado integral de superfície do segundo tipo de função f(x, y, z) ao longo do lado selecionado da superfície por variáveis x e y e denotados por ∫∫ f (x, y, z) dxdy. Assim, de acordo com
definição
superfície S nas variáveis x e y.
Da mesma forma, você pode definir integrais de superfície do segundo tipo sobre um lado selecionado da superfície S nas variáveis y e z, nas variáveis x e z:
∫∫ f(x, y, z) dydz, | ∫∫ f(x, y, z) dxdz. |
Sejam P (x, y, z), Q (x, y, z), R (x, y, z) funções integráveis sobre
superfície S nas variáveis y e z, x e z, x e y, respectivamente. Soma de integrais
∫∫ P(x, y, z) dydz, | ∫∫ Q(x, y, z) dxdz, | ∫∫ R(x, y, z) dxdy | |
é chamada de integral geral do segundo tipo e é denotada | |||
∫∫ P(x, y, z) dydz+ Q(x, y, z) dxdz+ R(x, y, z) dxdy. | |||
Como consideramos a superfície S bilateral e a integral se estende até um certo lado dela, então quando o lado da superfície de integração muda, a integral de superfície do segundo tipo muda de sinal para o oposto– esta é a sua diferença em relação à integral de superfície do primeiro tipo.
Cálculo de integrais de superfície do segundo tipo reduz-se ao cálculo de integrais duplas.
Deixe uma superfície lisa orientada (escolha o lado superior) S ser dada pela equação z = z (x, y), onde z (x, y) é contínuo em
área fechada S xy - projeção da superfície S no plano xOy; a função f(x, y, z) é contínua em S. Então a fórmula é válida
∫∫ f(x, y, z) dxdy= ∫∫ f(x, y, z(x, y)) dxdy, | ||||
Sexy | ||||
expressando a integral de superfície do segundo tipo sobre as variáveis x e | ||||
através do dobro. Se escolhermos o lado inferior da superfície S, então na frente |
||||
integral, um sinal de menos aparecerá no lado direito. | ||||
As fórmulas são igualmente válidas | ||||
∫∫ f(x, y, z) dydz= ∫∫ f(x(y, z), y, z) dydz, | ||||
S yz | ||||
∫∫ f(x, y, z) dxdz= ∫∫ f(x, y(x, z), z) dxdz, | ||||
Sxz | ||||
onde a superfície S | de acordo com as equações | x = x(y,z) | ||
y = y(x, z) e Syz | e S xz - | projeções da superfície S, respectivamente | ||
planos yOz e xOz.
Para calcular a integral de forma geral (4.6), as fórmulas (4.7)–(4.9) são usadas se a superfície S for projetada exclusivamente em todos
coordenar planos. Em casos mais complexos, a superfície S é dividida em partes que possuem as propriedades indicadas, e a integral geral é apresentada na forma de integrais sobre essas partes.
Exemplo 4.2.Calcular
∫∫ (y 2 + z 2 ) dxdy , onde S é o lado superior
superfície z = | 1 − x 2 | Corte plano |
||||||||
dados y = 0, y = 1. | ||||||||||
Solução. A equação x 2 + z 2 = 1 - |
||||||||||
um cilindro circular com geratriz é especificado, |
||||||||||
paralelo ao eixo Oy, e o plano y = 0 e |
||||||||||
y = 1 | paralelo | coordenada |
||||||||
plano xOz (Fig. | Projeção |
|||||||||
superfície S no plano xOy é |
||||||||||
retângulo S xy definido pelas desigualdades − 1 ≤ x ≤ 1, | 0 ≤ y ≤ 1. |
|||||||||
Então, pela fórmula (4.7) temos | ||||||||||
∫∫ (y2 + z2 ) dxdy= ∫∫ (y2 + (1 − x2 )) dxdy= ∫ dx∫ (y2 − x2 + 1) dy= |
||||||||||
Sexy | −1 | |||||||||
+ (1− x 2 )y ) | ||||||||||
= ∫ dx( | ||||||||||
−1 | ||||||||||
−x2)dx | ||||||||||||||||||||||||||||||
= ∫ ( | ||||||||||||||||||||||||||||||
−1 | −1 | |||||||||||||||||||||||||||||
Exemplo 4.3. Calcular | ||||||||||||||||||||||||||||||
∫∫ xdydz+ ydxdz+ zdxdy, onde S é o superior | ||||||||||||||||||||||||||||||
lado de parte do plano x + z − 1 = 0 | ||||||||||||||||||||||||||||||
cortado pelos planos y = 0, y = 4 e | ||||||||||||||||||||||||||||||
localizado no primeiro octante (Fig. 4.4). | ||||||||||||||||||||||||||||||
Solução. Projeção da superfície S em | ||||||||||||||||||||||||||||||
o plano xOy é o retângulo S xy, | ||||||||||||||||||||||||||||||
definido pelas desigualdades 0 ≤ x ≤ 1, | ||||||||||||||||||||||||||||||
0 ≤ y ≤ 4 . Projeção da superfície S em | ||||||||||||||||||||||||||||||
o plano yOz é um retângulo | S yz, definido pelas desigualdades |
|||||||||||||||||||||||||||||
0 ≤ z ≤ 1,0 ≤ y ≤ 4. Como o plano S é perpendicular ao plano |
||||||||||||||||||||||||||||||
xOz , então∫∫ ydxdz = 0. Então, pelas fórmulas (4.7) e (4.9) temos |
||||||||||||||||||||||||||||||
∫∫ xdydz+ ydxdz+ zdxdy= ∫∫ (1 − z) dydz+ |
||||||||||||||||||||||||||||||
S yz | ||||||||||||||||||||||||||||||
+ ∫∫ (1 − x) dxdy= ∫ dy∫ (1 − z) dz+ ∫ dy∫ (1 − x) dx= |
||||||||||||||||||||||||||||||
Sexy | ||||||||||||||||||||||||||||||
−z) | (1−x) | |||||||||||||||||||||||||||||
2 ∫ | dy = 4. |
|||||||||||||||||||||||||||||
= ∫ dy - | + ∫ dy - | |||||||||||||||||||||||||||||
4.4. Fórmula de Ostrogradsky. A fórmula de Ostrogradsky estabelece uma conexão entre a integral de superfície sobre uma superfície fechada e a integral tripla sobre a região espacial limitada por esta superfície.
Seja V uma região regular fechada limitada pela superfície S, e sejam as funções P(x, y, z), Q(x, y, z), R(x, y, z)
são contínuos junto com suas derivadas parciais de primeira ordem em uma determinada região. Então vale a seguinte fórmula:
∫∫∫( | ∂P | ∂Q | ∂ R ) dxdydz= ∫∫ Pdydz+ Qdxdz+ Rdxdy, (4.10) |
|||
∂x | ∂y | ∂z | ||||
chamado Fórmula de Ostrogradsky 1 .
Usando a fórmula de Ostrogradsky é conveniente calcular integrais de superfície sobre superfícies fechadas.
Exemplo 4.4. Usando a fórmula de Ostrogradsky, calcule
∫∫ xdydz + ydxdz + zdxdy , | Onde S | ||||||||||||||||||||||||||
lado da pirâmide | limitado | aviões | |||||||||||||||||||||||||
x + sim + z = 1, | x= 0,sim= 0, | z= 0 (Fig. 4.5). | |||||||||||||||||||||||||
De acordo com | |||||||||||||||||||||||||||
Ostrogradsky: | |||||||||||||||||||||||||||
P(x,sim,z)= x,P(x,sim,z)= sim,R(x,sim,z)= z. | |||||||||||||||||||||||||||
Então: ∂ P+ | ∂ P+ | ∂R | = 1+ 1+ 1= 3,e encontramos | ||||||||||||||||||||||||
∂x | ∂sim | ∂z | |||||||||||||||||||||||||
1− x | 1 −x−sim | ||||||||||||||||||||||||||
∫∫ xdydz + ydxdz + zdxdy = 3 ∫∫∫ dxdydz = 3 ∫ dx ∫ morrer | ∫ dz = | ||||||||||||||||||||||||||
1− x | 1 −x−sim | 1− x | |||||||||||||||||||||||||
= 3 ∫ dx ∫ morrer ∫ dz = 3 ∫ dx ∫ (1 − x − sim ) morrer = | |||||||||||||||||||||||||||
sim 2 | 1− x | ||||||||||||||||||||||||||
3 ∫ dx ( sim − xy − | |||||||||||||||||||||||||||
−2 x+1 | 3 (x− 1) | ||||||||||||||||||||||||||
= 3 ∫ (1 −x−x+x2 − | ) dx = | ∫ ( x − 1) 2 dx = | |||||||||||||||||||||||||
Observação 4.1. A conexão entre integrais de superfície do primeiro e segundo tipos é semelhante à conexão entre integrais curvilíneas:
∫∫ f ( x , sim , z ) dxdy = ∫∫ f ( x , sim , z )porqueα ds ,
∫∫ f ( x , sim , z ) dydz = ∫∫ f ( x , sim , z )porqueβ ds ,
∫∫ f ( x , sim , z ) dxdz = ∫∫ f ( x , sim , z )porqueγ ds ,
Onde porqueα ,porqueβ ,porqueγ - cossenos de direção da normal correspondente a
lado selecionado da superfície. ,sim) | contínua na área Sxy– projeções de superfície S |
||||||||||||||||||||||
para o avião xOi;eu | - contorno, | limitante | superfície | S ; eu – |
|||||||||||||||||||
projeção de linha espacial eu para o avião | xOi , | ser |
|||||||||||||||||||||
um canil limitando a área D. Vamos selecionar o lado superior |
|||||||||||||||||||||||
superfícies S. Se as funções P(x, sim, z), P(x, sim, z), R(x, sim, z) | contínuo |
||||||||||||||||||||||
juntamente com suas derivadas parciais de primeira ordem em |
|||||||||||||||||||||||
superfícies S, então a seguinte fórmula é válida: | |||||||||||||||||||||||
∫ PDX + Qdy + Rdz = | |||||||||||||||||||||||
= ∫∫ | (∂ P | ∂ P) dxdy + ( | ∂R | ∂ P) dydz + (∂ P | ∂ R) dxdz | ||||||||||||||||||
∂x | ∂sim | ∂sim | ∂z | ∂z | ∂x | ||||||||||||||||||
(eu- move-se em uma direção positiva) | chamado Fórmula |
||||||||||||||||||||||
Se como uma superfície S tomar área D na superfície xOi |
|||||||||||||||||||||||
(z= 0 ), então de (4.11) obtemos a fórmula de Green | ∂P | ∂ P) dxdy . | |||||||||||||||||||||
∫ P ( x , sim ) dx + P ( x , sim ) morrer = ∫∫ ( | |||||||||||||||||||||||
∂x | ∂sim | ||||||||||||||||||||||
Assim, a fórmula de Green é um caso especial da fórmula de Stokes. |
|||||||||||||||||||||||
Observe que a integral de superfície do segundo tipo na fórmula |
|||||||||||||||||||||||
Stokes (4.11) pode ser substituído pela integral de superfície do primeiro |
|||||||||||||||||||||||
tipo. Então esta fórmula assumirá a forma | |||||||||||||||||||||||
∫ PDX + Qdy + Rdz = | |||||||||||||||||||||||
∂P | ∂P | ∂R | ∂P | ∂P | ∂R | ||||||||||||||||||
= ∫∫ | )porque α + ( | )porque β + ( | )porque γ | ||||||||||||||||||||
∂x | ∂sim | ∂sim | ∂z | ∂z | ∂x | ds , | |||||||||||||||||
Onde porque α ,porque β ,porque γ , | significar | guias | cossenos | ||||||||||||||||||||
correspondente ao lado selecionado da superfície. | |||||||||||||||||||||||
usando a fórmula | calcular |
||||||||||||||||||||||
∫ x 2 sim 3 dx + morrer + zdz , | círculo, | dado pelas equações |
|||||||||||||||||||||
x 2 + sim 2 + 1, z = 0 . | Superfície S o lado superior do hemisfério serve |
||||||||||||||||||||||
x 2+ sim 2+ z 2= 1, | z> 0 (eu vai em uma direção positiva). |
||||||||||||||||||||||
Para casos em que a integração não ocorre sobre um segmento de curva, mas sobre uma superfície limitada. Assim como as integrais curvilíneas, as integrais de superfície são do primeiro e do segundo tipo.
Integral de superfície de primeiro tipo escrito na forma
Onde f(M) = f(x,y,z) é uma função de três variáveis, e a superfície σ - área de integração desta função. Se f(x,y,z) é igual à unidade, então a integral da superfície é igual à área da superfície.
Imagine um girassol bastante grande com sementes muito pequenas. Então, a partir da soma das superfícies de sementes muito pequenas localizadas na superfície de um girassol, pode-se calcular a superfície do girassol - esta pode ser uma interpretação simplificada da integral de superfície. Por que é que?
Vamos passar para uma definição mais formal de integral de superfície. Superfície σ dividido em n partes com áreas Δ σ 1 , Δ σ 2 , ..., Δ σ n. Se você selecionar um ponto arbitrário em cada superfície parcial (semente) Meu com coordenadas ( ζ eu, η eu, ς eu ,), então podemos resumir
Esta soma é chamada de soma integral da função f(M) na superfície σ . Agora vamos maximizar o número dessas peças pequenas e o maior diâmetro Δ σ eu- pelo contrário, reduza. Se a soma integral como o maior dos diâmetros das peças tende a zero (isto é, como já observamos, todas as peças são muito pequenas) tem um limite, então esse limite é chamado integral de superfície de primeiro tipo da função f(M) na superfície σ .
Cálculo da integral de superfície de primeiro tipo
Deixe a superfície σ dado pela equação z = z(x, sim) , sua projeção no plano xOié a área Dxy, enquanto a função z = z(x, sim) e suas derivadas parciais são contínuas na região Dxy.
Exemplo 1.
Onde σ - parte do plano no primeiro octante.
Solução. Desenho:
Da equação do plano obtemos a expressão “zet”: 
.
Então as derivadas parciais são: e
.
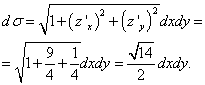Superfície σ é o triângulo mostrado no desenho abc, e sua projeção no plano xOi- triângulo AOB, que é limitado por linhas retas x = 0 , sim= 0 e 3 x + sim= 6. Vamos passar da integral de superfície para a integral dupla e resolvê-la:
.
O conceito de integral de superfície de segundo tipo
Antes de passar à definição de integral de superfície de segundo tipo, é necessário familiarizar-se com os conceitos de lados de superfícies e superfícies orientadas.
Deixe uma superfície lisa ser dada no espaço σ . Vamos escolher um ponto arbitrário nesta superfície M e desenhe o vetor normal à superfície através dele. Através do ponto M também faremos na superfície σ um contorno arbitrário que não tem pontos comuns com o limite da superfície σ . Ponto final M junto com o vetor normal, nos moveremos ao longo do contorno para que o vetor normal seja constantemente perpendicular à superfície σ . Após o retorno do ponto M para a posição inicial, dois casos são possíveis: a direção do vetor normal permanecerá a mesma ou mudará para o oposto.
Se a direção do vetor normal não mudar, então a superfície σ chamado bilateral. Se, ao percorrer o contorno, a direção do vetor normal muda para o oposto, então a superfície é chamada unilateral. Superfícies de dupla face são chamadas de superfícies orientadas, superfícies unilaterais são chamadas de superfícies não orientadas.
Um exemplo de superfície unilateral é uma tira de Möbius (na foto acima), que pode ser feita de uma tira de papel com um lado girado 180 graus e depois as pontas coladas. E aqui está o que é importante aqui: para uma superfície unilateral, o conceito de integral de superfície do segundo tipo não é introduzido .
Portanto, consideraremos apenas superfícies bilaterais. Exemplos de superfícies bilaterais são planos, esferas, elipsóides e parabolóides.
O lado positivo de uma superfície bilateral determina a direção do vetor normal. O lado oposto da superfície é chamado negativo. O lado positivo de uma superfície é o seu lado superior. Se os vetores normais unitários formam ângulos agudos com o eixo onça, então o lado superior da superfície é selecionado z = z(x, sim) , se os ângulos forem obtusos, então o lado inferior da superfície.
Como no caso da integral de superfície do primeiro tipo, a superfície pode ser dividida em n peças. Ao formular o conceito de integral de superfície de primeiro tipo, a soma integral incluiu as áreas de cada uma das partes pelas quais os valores da função foram multiplicados f(Meu). No caso de uma integral de superfície do segundo tipo, as áreas das próprias partes não são tomadas, mas as áreas de suas projeções em planos coordenados . E para distinguir a função de três variáveis de uma integral do primeiro tipo, denotamos R(x,sim,z) . Então a soma integral será escrita da seguinte forma:
,
onde Δ éeu- as áreas das projeções mencionadas de partes da lateral da superfície no eixo de coordenadas (por enquanto vamos assumir que no eixo xOi).
Com tais convenções e notação, a definição de uma integral de superfície de segundo tipo é semelhante à definição de uma integral de primeiro tipo. A saber: uma integral de superfície do segundo tipo é o limite de uma dada soma integral, pois o maior diâmetro das partes da superfície em consideração tende a zero.
Está escrito assim:
.
Neste caso a função R(x,sim,z) integrável sobre variáveis x E sim, uma vez que partes da superfície foram projetadas no plano xOi.
Da mesma forma, podemos escrever duas outras integrais de superfície do segundo tipo:
(função P(x,sim,z) integrável sobre variáveis sim E z yOz),
(função P(x,sim,z) integrável sobre variáveis z E x, uma vez que partes da superfície são projetadas no plano zOx).
A soma dessas integrais
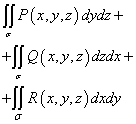
chamado integral geral de superfície de segundo tipo e é designado
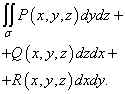
Cálculo da integral de superfície de segundo tipo
Uma integral de superfície de segundo tipo é calculada decompondo a integral de superfície geral de segundo tipo na soma das integrais de superfície (ver final do parágrafo anterior) e reduzindo cada uma delas a uma integral dupla.
Vamos considerar em detalhes o cálculo da integral
.
Deixe a superfície σ dado pela equação z = z(x, sim) . Denotamos o lado positivo da superfície, o lado negativo e a projeção no plano xOi - Dxy.
Assim, obtemos uma fórmula para calcular a integral de superfície do segundo tipo:
Se o lado negativo da superfície for selecionado, o sinal da integral muda:
As outras duas integrais separadas - termos da integral - são calculadas de forma semelhante:
Exemplo 2.
,
Onde σ - a parte superior de uma parte do avião, cortada por planos sim= 0 e sim= 4 e localizado no primeiro octante.
Solução. O desenho está na foto acima. Por definição, obtemos a soma de três integrais duplas:
A segunda integral é igual a zero, pois o plano σ paralelo ao eixo Oi. Portanto, encontramos a primeira e a terceira integrais:
Resta apenas somar todas as integrais individuais e obter a integral geral de superfície do segundo tipo:
.
Se você precisar calcular uma integral de superfície do segundo tipo sobre uma superfície fechada, você pode ir para integral tripla, usando a fórmula de Ostrogradsky. Então, se as funções P(x,y,z) , P(x,y,z) E R(x,y,z) e suas derivadas parciais, são funções contínuas no domínio C, que é delimitado por uma superfície fechada σ , então, ao integrar na parte externa da superfície, a igualdade
Exemplo 3. Calcular integral de superfície de segundo tipo
,
Onde σ - o lado externo da superfície de um cone formado por uma superfície e um plano z = 2 .
Solução. Esta superfície é a superfície de um cone com raio R= 2 e altura h= 2. Esta é uma superfície fechada, então você pode usar a fórmula de Ostrogradsky. Porque P = 3x , P = 4sim , R = −z, então as derivadas parciais , , .
Passamos para a integral tripla, que resolvemos:
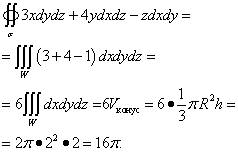
Mais exemplos de cálculo de integrais de superfície
Exemplo 4. Calcular integral de superfície do primeiro tipo
Onde σ - superfície lateral do cone em .
Solução. Como as derivadas parciais 
,
, Que
Reduzimos esta integral de superfície a uma integral dupla:
Projeção de uma superfície em um plano xOié uma circunferência com centro na origem e raio R= 2, portanto, ao calcular a integral dupla, passamos para o sistema de coordenadas polares. Para fazer isso, vamos alterar as variáveis:
Obtemos a seguinte integral, que finalmente resolvemos:
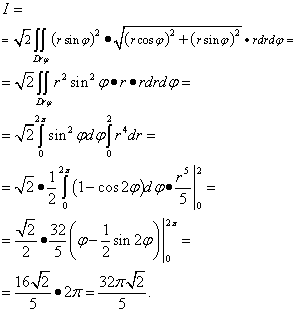
Exemplo 5. Calcular integral de superfície de segundo tipo
,
Onde σ - a parte superior do triângulo formado pela intersecção do plano com os planos coordenados.
Solução. Vamos dividir esta integral de superfície pela soma de duas integrais
, Onde
.
Para calcular a integral EU1 σ para o avião yOz. A projeção é um triângulo OCB, que está no avião yOz limitar linhas retas ou, sim= 0 e z= 0. Da equação do plano é derivado. Portanto podemos calcular a integral EU1 :
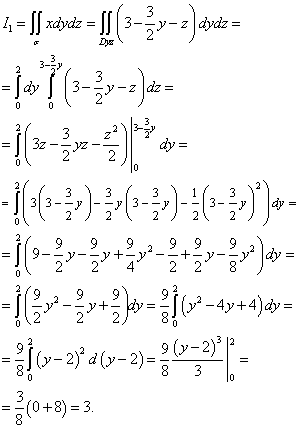
Para calcular a integral EU2 , vamos construir uma projeção de superfície σ para o avião zOx. A projeção é um triângulo COA, que é delimitado por linhas retas ou , x= 0 e z= 0. Calculamos:
Somamos as duas integrais resultantes e finalmente obtemos esta integral de superfície:
.
Exemplo 6. Calcular integral de superfície de segundo tipo
,
Onde σ
- a superfície externa de uma pirâmide formada por um plano 
e coordenar planos.
Exemplo 3.3. Calcule o trabalho de um campo vetorial
a = 2x 2 sim eu – xy 2 j
da origem O ao ponto A(1;1), se o movimento ocorrer ao longo de: A) segmento de linha; b) arcos de parábola; V) linha tracejada OBA, onde B(1;0) (ver Fig. 3.1).
Solução . A) A equação da reta OA tem a forma y=x. Deixar x=t, então a equação da linha reta na forma paramétrica terá a forma:
x=t, y=t,
e ao passar de A para B o parâmetro t mudará de 0 para 1. Então o trabalho realizado será igual a
b) Deixar x=t 2 , s=t, Então
x=t 2 , s=t, 0£ t£ 1 .
.
V) A equação da reta (OB) é sim=0 (0£ x£1); a equação da reta (BA) tem a forma x=1 (0£ sim 1€). Então
, 
.
Como resultado, obtemos,
.
Comente. Se no caso de campos bidimensionais a equação da linha é descrita pela equação sim=sim(x), e a variável x varia de a antes b, então a integral curvilínea do 2º será calculada pela fórmula:
. (3.9)
O exemplo anterior poderia ser resolvido usando esta fórmula sem introduzir o parâmetro t.
Exemplo 3.4. Calcular integral
,
onde L é o arco da parábola y=x 2 +1 do ponto A(0;1) ao ponto B(2;5).
Solução . Vamos fazer um desenho (ver Fig. 3.2). Da equação da parábola obtemos y" = 2x. Já que no arco de uma parábola AB variável x muda de 0 para 2, então a integral curvilínea, de acordo com a fórmula (3.9), terá a forma
4. INTEGRAIS DE SUPERFÍCIE
4.1. Integrais de superfície de primeiro tipo
A integral de superfície de 1º tipo é uma generalização da integral dupla e é introduzida de forma semelhante. Considere alguma superfície S, suave ou suave por partes, e suponha que a função f( x,y,z) é definido e limitado nesta superfície. Vamos dividir esta superfície em n partes arbitrárias. A área de cada parcela é denotada por D e eu. Em cada seção selecionamos um ponto com coordenadas ( x eu, y eu, z eu) e calcule o valor da função em cada ponto. Depois disso, criamos a soma integral:
.
Se houver um limite de somas integrais em n®¥ (neste caso máx. D e eu®0), ou seja, tal limite não depende nem do método de particionamento nem da escolha dos pontos médios, então tal limite é denominado integral de superfície de primeiro tipo :
. (4.1)
Se a função f( x,y,z) é contínuo na superfície S, então o limite (4.1) existe.
Se a função integrando f( x,y,z)º1, então a integral de superfície de 1º tipo é igual à área de superfície S:
. (4.2)
Suponhamos que seja introduzido um sistema de coordenadas cartesianas e qualquer linha reta paralela ao eixo Oz, pode atravessar a superfície S apenas em um ponto. Então a equação da superfície S pode ser escrito na forma
z = z(x,y)
e é projetado exclusivamente no avião xOi. Como resultado, a integral de superfície do 1º tipo pode ser expressa em termos da integral dupla
.
(4.3)
Exemplo 4.1. Calcular integral
,
Onde S– parte da superfície cônica z 2 =x 2 +sim£ 2,0 z£ 1.
Solução. Nós temos
Então a integral necessária é transformada em uma integral dupla
Onde Sexy- círculo x 2 +sim 2 £ 1. É por isso
.
4.2. Integrais de superfície de segundo tipo
Deixe um campo vetorial ser especificado em alguma região
a = um x eu + sim j + uma z k
e qualquer superfície dupla face S. Vamos dividir a superfície de alguma forma em áreas elementares D S eu. Em cada site escolhemos um ponto arbitrário P eu e compor a soma integral:
, (4.4)
Onde n (P eu) – vetor normal a uma determinada superfície em um ponto P eu. Se houver um limite para tal soma em D S eu®0, então esse limite é chamado integral de superfície de 2º tipo (ou fluxo campo vetorial a através da superfície S) e é denotado pelo símbolo
ou ,
Onde d é =n ds.
Como o vetor normal unitário tem cossenos direcionais como suas coordenadas n =(cosa, cosb, cosg). Que
Assim, o cálculo de integrais de superfície de 2º tipo pode ser reduzido ao cálculo de integrais de superfície de 1º tipo. No entanto, o que Ao contrário das integrais de superfície de 1º tipo, as integrais de 2º tipo dependem da escolha do lado da superfície. A transição para o outro lado da superfície altera a direção da normal à superfície e, consequentemente, o sinal da integral.
Considere a integral
.
Deixe a equação da superfície ter a forma z=j( x,y) e o lado positivo desta superfície será considerado aquele cuja normal se forma com o eixo O z canto afiado. Então
custo ds = dxdy.
Portanto, a integral em consideração pode ser escrita na forma
.
Substituindo z por j( x,y), chegamos à integral dupla
,
Onde Sexy– projeção de superfície S para o avião xOi.
