Fórmula para calcular a mediana nas estatísticas. Características estruturais das séries de distribuição de variação

19.04.2022

TESTE

Sobre o tema: "Moda. Mediana. Métodos para seu cálculo"

Introdução

Os valores médios e os indicadores de variação associados desempenham um papel muito importante nas estatísticas, o que se deve ao objeto do seu estudo. Portanto, este tema é um dos centrais do curso.

A média é uma medida resumida muito comum nas estatísticas. Isso se explica pelo fato de que somente com a ajuda da média uma população pode ser caracterizada por uma característica quantitativamente variável. Nas estatísticas, o valor médio é uma característica generalizante de um conjunto de fenômenos semelhantes com base em alguma característica quantitativamente variável. A média mostra o nível dessa característica por unidade da população.

Ao estudar fenômenos sociais e tentar identificar seus traços característicos e típicos em condições específicas de lugar e tempo, os estatísticos utilizam amplamente valores médios. Usando médias, você pode comparar diferentes populações entre si de acordo com características variadas.

As médias utilizadas nas estatísticas pertencem à classe das médias de potência. Das médias de potência, a média aritmética é a mais usada, e menos frequentemente a média harmônica; A média harmônica é usada apenas no cálculo das taxas médias de dinâmica, e a média quadrada é usada apenas no cálculo dos índices de variação.

A média aritmética é o quociente da divisão da soma das variantes pelo seu número. É utilizado nos casos em que o volume de uma característica variável para toda a população é formado como a soma dos valores característicos de suas unidades individuais. A média aritmética é o tipo de média mais comum, pois corresponde à natureza dos fenômenos sociais, onde o volume das características variáveis no agregado é na maioria das vezes formado precisamente como a soma dos valores característicos das unidades individuais da população .

De acordo com sua propriedade definidora, a média harmônica deve ser utilizada quando o volume total do atributo é formado como a soma dos valores inversos da variante. É utilizado quando, dependendo do material, os pesos não devem ser multiplicados, mas sim divididos em opções ou, o que dá no mesmo, multiplicados pelo seu valor recíproco. A média harmônica nestes casos é a recíproca da média aritmética dos valores recíprocos da característica.

A média harmônica deve ser utilizada nos casos em que não são utilizadas como pesos as unidades da população - os portadores da característica, mas sim os produtos dessas unidades pelo valor da característica.

1. Definição de moda e mediana em estatísticas

As médias aritméticas e harmônicas são características generalizantes da população de acordo com uma ou outra característica variável. As características descritivas auxiliares da distribuição de uma característica variável são a moda e a mediana.

Nas estatísticas, uma moda é o valor de uma característica (variante) encontrada com mais frequência em uma determinada população. Numa série de variação, esta será a opção com maior frequência.

Nas estatísticas, a mediana é a opção que está no meio da série de variação. A mediana divide a série ao meio; em ambos os lados (para cima e para baixo) há o mesmo número de unidades populacionais.

Moda e mediana, em contraste com as médias de potência, são características específicas; seu significado é atribuído a qualquer opção específica na série de variação.

A moda é usada nos casos em que é necessário caracterizar o valor de uma característica que ocorre com mais frequência. Se for necessário, por exemplo, saber qual é o salário mais comum numa empresa, o preço de mercado a que foi vendido o maior número de mercadorias, o tamanho do calçado mais procurado pelos consumidores, etc., em nesses casos recorrem à moda.

A mediana é interessante porque mostra o limite quantitativo do valor de uma característica variável, que foi atingido por metade da população. Deixe o salário médio dos funcionários do banco ser de 650.000 rublos. por mês. Essa característica pode ser complementada se dissermos que metade dos trabalhadores recebia um salário de 700.000 rublos. e superior, ou seja, Vamos dar a mediana. Moda e mediana são características típicas em casos onde as populações são homogêneas e em grande número.

2. Encontrando a moda e a mediana em uma série de variação discreta

Encontrar a moda e a mediana em uma série de variação, onde os valores de uma característica são dados por determinados números, não é muito difícil. Vejamos a Tabela 1 com a distribuição das famílias por número de filhos.

Tabela 1. Distribuição das famílias por número de filhos

Obviamente, neste exemplo, a moda será uma família com dois filhos, pois o valor desta opção corresponde ao maior número de famílias. Podem existir distribuições onde todas as opções ocorrem com a mesma frequência, caso em que não existe moda, ou, por outras palavras, podemos dizer que todas as opções são igualmente modais. Em outros casos, não uma, mas duas opções podem ser de maior frequência. Então haverá dois modos, a distribuição será bimodal. Distribuições bimodais podem indicar heterogeneidade qualitativa da população de acordo com a característica em estudo.

Para encontrar a mediana em uma série de variação discreta, é necessário dividir a soma das frequências pela metade e adicionar ½ ao resultado. Assim, na distribuição de 185 famílias pelo número de filhos, a mediana será: 185/2 + ½ = 93, ou seja, A 93ª opção, que divide a linha ordenada ao meio. Qual é o significado da 93ª opção? Para saber é preciso acumular frequências, começando pelas menores opções. A soma das frequências da 1ª e 2ª opções é 40. É claro que não existem 93 opções aqui. Se somarmos a frequência da 3ª opção a 40, obtemos uma soma igual a 40 + 75 = 115. Portanto, a 93ª opção corresponde ao terceiro valor da característica variável, e a mediana será uma família com dois filhos.

A moda e a mediana neste exemplo coincidiram. Se tivéssemos uma soma par de frequências (por exemplo, 184), então, usando a fórmula acima, obteríamos o número da opção mediana, 184/2 + ½ =92,5. Como não existem opções fracionárias, o resultado indica que a mediana está no meio do caminho entre 92 e 93 opções.

3. Cálculo da moda e mediana em séries de variação intervalar

A natureza descritiva da moda e da mediana deve-se ao facto de não compensarem os desvios individuais. Correspondem sempre a uma opção específica. Portanto, a moda e a mediana não requerem cálculos para saber se todos os valores do atributo são conhecidos. Porém, em uma série de variação intervalar, cálculos são usados para encontrar o valor aproximado da moda e da mediana dentro de um determinado intervalo.

Para calcular um determinado valor do valor modal de uma característica contida em um intervalo, use a fórmula:

M o = X Mo + i Mo *(f Mo – f Mo-1)/((f Mo – f Mo-1) + (f Mo – f Mo+1)),

Onde XMo é o limite mínimo do intervalo modal;

i Mo – o valor do intervalo modal;

f Mo – frequência do intervalo modal;

f Mo-1 – frequência do intervalo anterior ao modal;

f Mo+1 – frequência do intervalo seguinte ao modal.

Vamos mostrar o cálculo da moda usando o exemplo dado na Tabela 2.

Tabela 2. Distribuição dos trabalhadores da empresa por cumprimento dos padrões de produção

Para encontrar a moda, primeiro determinamos o intervalo modal desta série. O exemplo mostra que a frequência mais alta corresponde ao intervalo onde as variantes estão na faixa de 100 a 105. Este é o intervalo modal. O valor do intervalo modal é 5.

Substituindo os valores numéricos da Tabela 2 na fórmula acima, obtemos:

M o = 100 + 5 * (104 -12)/((104 – 12) + (104 – 98)) = 108,8

O significado desta fórmula é o seguinte: o valor daquela parte do intervalo modal que precisa ser adicionado ao seu limite mínimo é determinado dependendo da magnitude das frequências dos intervalos anteriores e subsequentes. Neste caso, adicionamos 8,8 a 100, ou seja, mais de meio intervalo porque a frequência do intervalo anterior é menor que a frequência do intervalo subsequente.

Vamos agora calcular a mediana. Para encontrar a mediana em uma série de variação intervalar, primeiro determinamos o intervalo em que ela está localizada (intervalo mediano). Tal intervalo será aquele cuja frequência cumulativa seja igual ou superior à metade da soma das frequências. As frequências cumulativas são formadas pela soma gradual das frequências, partindo do intervalo com o menor valor do atributo. Metade da soma das frequências é 250 (500:2). Portanto, de acordo com a Tabela 3, o intervalo mediano será o intervalo com valor salarial de 350.000 rublos. até 400.000 rublos.

Tabela 3. Cálculo da mediana nas séries de variação intervalar

Antes desse intervalo, a soma das frequências acumuladas era 160. Portanto, para obter o valor mediano é necessário somar mais 90 unidades (250 – 160).

Mediana Eu eles chamam o valor do atributo que fica no meio da série classificada e o dividem em duas partes iguais em número de unidades. Assim, na linha classificada da distribuição, metade da linha possui valores de atributos superiores à mediana, a outra metade é menor que a mediana.

A mediana é usada em vez da média aritmética quando as opções extremas da série classificada (menor e maior) em comparação com o resto são excessivamente grandes ou excessivamente pequenas.

EM discreto em uma série de variação contendo um número ímpar de unidades, a mediana é igual à variante da característica que possui o número:
,
onde N é o número de unidades populacionais.
Numa série discreta constituída por um número par de unidades populacionais, a mediana é definida como a média das opções que possuem números e:
.
Na distribuição dos trabalhadores por tempo de serviço, a mediana é igual à média das opções com números 10 na série ordenada: 2 = 5 e 10: 2 + 1 = 6. As opções para a quinta e sexta características são iguais a 4 anos, portanto
Do ano
Ao calcular a mediana em intervalo primeira linha encontrada intervalo mediano, (ou seja, contendo a mediana), para o qual são utilizadas frequências ou frequências acumuladas. A mediana é um intervalo cuja frequência acumulada é igual ou superior à metade do volume total da população. O valor mediano é então calculado usando a fórmula:
,
onde está o limite inferior do intervalo mediano;
– largura do intervalo mediano;
– frequência acumulada do intervalo anterior à mediana;
– frequência do intervalo mediano.
Vamos calcular a mediana da distribuição dos trabalhadores por salário (ver palestra “Resumo e agrupamento de dados estatísticos”).
A mediana é a faixa salarial de 800-900 UAH, já que sua frequência acumulada é 17, o que ultrapassa a metade da soma de todas as frequências (). Então
Eu=800+100 UAH.
O valor obtido indica que metade dos trabalhadores tem salários inferiores a 875 UAH, mas está acima da média.
Para determinar a mediana, você pode usar frequências cumulativas em vez de frequências cumulativas.
A mediana, assim como a moda, não depende dos valores extremos da variante, portanto também é utilizada para caracterizar o centro em séries de distribuição com limites incertos.
Propriedade mediana : a soma dos valores absolutos dos desvios da mediana é menor do que qualquer outro valor (incluindo a média aritmética):

Esta propriedade do canteiro central é usada no transporte ao projetar a localização de paradas de bonde e trólebus, postos de gasolina, pontos de encontro, etc.
Exemplo. São 10 garagens ao longo dos 100 km da rodovia. Para projetar a construção de um posto de gasolina, foram coletados dados sobre o número de viagens previstas ao posto de gasolina para cada garagem.
Tabela 2 - Dados sobre o número de idas ao posto de gasolina para cada garagem.

É necessária a instalação de posto de gasolina para que a quilometragem total dos veículos para reabastecimento seja mínima.
Opção 1. Se um posto de gasolina estiver localizado no meio da rodovia, ou seja, no quilômetro 50 (centro da faixa de variação do atributo), então a quilometragem, levando em consideração o número de viagens, será:
a) em uma direção:
;
b) no oposto:
;
c) quilometragem total nos dois sentidos: .

Opção 2. Se um posto de gasolina estiver localizado no trecho intermediário da rodovia, determinado pela fórmula da média aritmética, levando em consideração o número de viagens:

A mediana pode ser determinada graficamente, utilizando o acumulado (ver aula “Resumo e agrupamento de dados estatísticos”). Para fazer isso, a última ordenada, igual à soma de todas as frequências ou frequências, é dividida pela metade. A partir do ponto resultante, uma perpendicular é restaurada até cruzar com o acumulado. A abscissa do ponto de intersecção fornece o valor mediano.

A função MEDIAN no Excel é usada para analisar um intervalo de valores numéricos e retorna um número que é o meio do conjunto que está sendo examinado (a mediana). Ou seja, esta função divide condicionalmente um conjunto de números em dois subconjuntos, o primeiro dos quais contém números menores que a mediana e o segundo - mais. A mediana é um dos vários métodos para determinar a tendência central de um intervalo de interesse.

Exemplos de uso da função MEDIAN no Excel

Ao estudar faixas etárias de estudantes, foram utilizados dados de um grupo de estudantes selecionados aleatoriamente em uma universidade. A tarefa é determinar a idade média dos alunos.

Dados iniciais:

Fórmula para cálculo:

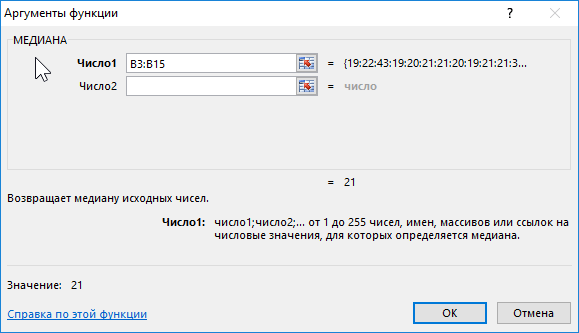
Descrição do argumento:

B3:B15 – faixa etária estudada.

Resultado:

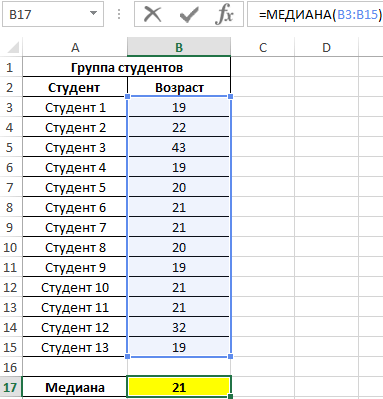
Ou seja, há alunos no grupo cuja idade é inferior a 21 anos e superior a este valor.

Comparando as funções MEDIAN e AVERAGE para calcular o valor médio

Durante as rondas noturnas no hospital, a temperatura corporal de cada paciente foi medida. Demonstre a utilidade de usar o parâmetro mediana em vez do valor médio para examinar uma faixa de valores obtidos.

Dados iniciais:

Fórmula para encontrar a média:

Fórmula para encontrar a mediana:

Como pode ser visto pelo valor médio, em média a temperatura dos pacientes está acima do normal, mas isso não é verdade. A mediana mostra que pelo menos metade dos pacientes apresenta temperatura corporal normal, não ultrapassando 36,6.

Atenção! Outro método para determinar a tendência central é a moda (o valor que ocorre com mais frequência na faixa em estudo). Para determinar a tendência central no Excel, você deve usar a função MODE. Observe que neste exemplo os valores da mediana e da moda são iguais:

Ou seja, o valor mediano que divide um conjunto em subconjuntos de valores menores e maiores também é o valor que ocorre com mais frequência no conjunto. Como você pode ver, a maioria dos pacientes tem temperatura de 36,6.

Um exemplo de cálculo da mediana em análise estatística no Excel

Exemplo 3. Há 3 vendedores trabalhando numa loja. Com base nos resultados dos últimos 10 dias, é necessário determinar o funcionário que receberá o bônus. Na escolha do melhor funcionário, leva-se em consideração o grau de eficiência do seu trabalho e não a quantidade de mercadorias vendidas.

Tabela de dados original:

Para caracterizar a eficiência, utilizaremos três indicadores ao mesmo tempo: valor médio, mediana e moda. Vamos determiná-los para cada funcionário usando as fórmulas AVERAGE, MEDIAN e MODE, respectivamente:

Para determinar o grau de dispersão dos dados, utilizamos um valor que é o valor total do módulo da diferença entre o valor médio e a moda, valor médio e mediana, respectivamente. Ou seja, o coeficiente x=|av-med|+|av-mod|, onde:

av – valor médio;
med – mediana;
moda - moda.

Vamos calcular o valor do coeficiente x para o primeiro vendedor:

Faremos cálculos de forma semelhante para outros vendedores. Resultados:

Vamos determinar o vendedor a quem o bônus será concedido:

Nota: A função SMALL retorna o primeiro valor mínimo do intervalo considerado de valores dos coeficientes x.

O coeficiente x é uma certa característica quantitativa da estabilidade do trabalho dos vendedores, introduzida pelo economista da loja. Com sua ajuda, foi possível determinar o intervalo com os menores desvios de valores. Este método demonstra como três métodos para determinar a tendência central podem ser usados ao mesmo tempo para obter resultados mais confiáveis.

Recursos de uso da função MEDIAN no Excel

A função possui a seguinte sintaxe:

MEDIANA(número1; [número2];...)

Descrição dos argumentos:

número1 é um argumento obrigatório que caracteriza o primeiro valor numérico contido no intervalo em estudo;
[número2] – segundo opcional (e argumentos subsequentes, até 255 argumentos no total), caracterizando o segundo e subsequentes valores do intervalo em estudo.

Notas 1:

Ao fazer cálculos, é mais conveniente transferir toda a gama de valores que estão sendo estudados de uma só vez, em vez de inserir argumentos sequencialmente.
Os argumentos aceitos são dados numéricos, nomes contendo números, dados de tipo de referência e matrizes (por exemplo, =MEDIAN((1,2,3,5,7,10))).
No cálculo da mediana são levadas em consideração as células que contêm valores vazios ou os lógicos TRUE, FALSE, que serão interpretados como os valores numéricos 1 e 0, respectivamente. Por exemplo, o resultado da execução de uma função com valores lógicos nos argumentos (TRUE; FALSE) é equivalente ao resultado da execução dela com argumentos (1;0) e é igual a 0,5.
Se um ou mais argumentos da função aceitarem valores de texto que não podem ser convertidos em valores numéricos ou contiverem códigos de erro, a função retornará o código de erro #VALUE!.
Outras funções do Excel podem ser usadas para determinar a mediana de uma amostra: PERCENTILE.IN, QUARTILE.IN, MAX Exemplos de uso:

=PERCENTIL.IN(A1:A10,0,5), pois por definição a mediana é o percentil 50.
=QUARTIL.ON(A1:A10;2), pois a mediana é o 2º quartil.
=ALTO(A1:A9,CONTAR(A1:A9)/2), mas somente se o número de números no intervalo for um número ímpar.

Notas 2:

Se na faixa em estudo todos os números estiverem distribuídos simetricamente em torno da média, a média aritmética e a mediana dessa faixa serão equivalentes.
Com grandes desvios de dados no intervalo (“dispersão” de valores), a mediana reflete melhor a tendência na distribuição dos valores do que a média aritmética. Um excelente exemplo é o uso da mediana para determinar o nível real de salários da população de um estado em que os funcionários ganham uma ordem de grandeza mais do que os cidadãos comuns.
A faixa de valores em estudo pode conter:

Um número ímpar de números. Neste caso, a mediana será um único número que divide o intervalo em dois subconjuntos de valores maiores e menores, respectivamente;
Número par de números. Em seguida, a mediana é calculada como a média aritmética de dois valores numéricos que dividem o conjunto nos dois subconjuntos indicados acima.

Salários em vários setores da economia, níveis de temperatura e precipitação no mesmo território durante períodos de tempo comparáveis, rendimento das culturas cultivadas em diferentes regiões geográficas, etc. No entanto, a média não é de forma alguma o único indicador generalizante - em alguns casos para uma avaliação mais precisa, um valor adequado é a mediana. Nas estatísticas, é amplamente utilizado como característica descritiva auxiliar da distribuição de uma característica em uma determinada população. Vamos descobrir como ele difere da média e também por que é necessário utilizá-lo.

Mediana em estatística: definição e propriedades

Imagine a seguinte situação: 10 pessoas trabalham em uma empresa junto com o diretor. Os trabalhadores comuns recebem 1.000 UAH, e seu gerente, que também é o proprietário, recebe 10.000 UAH. Se calcularmos a média aritmética, verifica-se que o salário médio nesta empresa é de 1.900 UAH. Esta afirmação será verdadeira? Ou tomemos este exemplo: na mesma enfermaria há nove pessoas com temperatura de 36,6 °C e uma pessoa com temperatura de 41 °C. A média aritmética neste caso é igual a: (36,6*9+41)/10 = 37,04 °C. Mas isso não significa que todos os presentes estejam doentes. Tudo isto sugere que a média por si só muitas vezes não é suficiente, e é por isso que a mediana é usada em adição a ela. Nas estatísticas, esse indicador é denominado opção que está localizada exatamente no meio da série de variação ordenada. Se calcularmos para nossos exemplos, obteremos 1.000 UAH, respectivamente. e 36,6°C. Em outras palavras, uma mediana nas estatísticas é um valor que divide uma série ao meio de tal forma que em ambos os lados dela (para baixo ou para cima) haja o mesmo número de unidades em uma determinada população. Devido a esta propriedade, este indicador tem vários outros nomes: percentil 50 ou quantil 0,5.

Como encontrar a mediana nas estatísticas

O método de cálculo deste valor depende muito do tipo de série de variação que temos: discreta ou intervalar. No primeiro caso, a mediana é encontrada de forma bastante simples nas estatísticas. Tudo o que você precisa fazer é encontrar a soma das frequências, dividir por 2 e depois adicionar ½ ao resultado. Seria melhor explicar o princípio de cálculo usando o exemplo a seguir. Digamos que agrupamos dados sobre fertilidade e queremos descobrir qual é a mediana.

Número do grupo familiar por número de filhos	Número de famílias

Após alguns cálculos simples, descobrimos que o indicador necessário é: 195/2 + ½ = opção. Para descobrir o que isso significa, você deve acumular frequências sequencialmente, começando pelas menores opções. Portanto, a soma das duas primeiras linhas nos dá 30. É claro que não existem 98 opções aqui. Mas se você somar a frequência da terceira opção (70) ao resultado, obtém uma soma igual a 100. Contém exatamente a 98ª opção, o que significa que a mediana será uma família que tem dois filhos.

Quanto às séries intervalares, costuma-se utilizar a seguinte fórmula:

M e = X Me + i Me * (∑f/2 - S Me-1)/f Me, em que:

X Me - primeiro valor do intervalo mediano;
∑f - número de séries (soma de suas frequências);
i Ме - o valor do intervalo mediano;
f Me - frequência da faixa mediana;
S Ме-1 é a soma das frequências cumulativas nas faixas anteriores à mediana.

Novamente, é muito difícil entender sem um exemplo. Suponha que haja dados sobre o valor

Salário, mil rublos.		Frequências acumuladas

Para usar a fórmula acima, primeiro precisamos determinar o intervalo mediano. Como tal faixa, escolha aquela cuja frequência acumulada exceda metade da soma total das frequências ou seja igual a ela. Assim, dividindo 510 por 2, descobrimos que este critério corresponde ao intervalo com valor salarial de 250.000 rublos. até 300.000 rublos. Agora você pode substituir todos os dados na fórmula:

M e = X Me + i Me * (∑f/2 - S Me-1)/f Me = 250 + 50 * (510/2 - 170) / 115 = 286,96 mil rublos.

Esperamos que nosso artigo tenha sido útil e que agora você tenha uma compreensão clara do que é uma mediana nas estatísticas e como ela deve ser calculada.

Um número que caracteriza uma amostra (por exemplo, um conjunto de números). Se todos os elementos da amostra forem diferentes, então a mediana é o número da amostra tal que exatamente metade dos elementos da amostra são maiores que ele e a outra metade é menor que ele. De forma mais geral, a mediana pode ser encontrada ordenando os elementos de uma amostra em ordem crescente ou decrescente e tomando o elemento do meio. Por exemplo, a amostra (11, 9, 3, 5, 5) após ordenada se transforma em (3, 5, 5, 9, 11) e sua mediana é o número 5. Se a amostra tiver um número par de elementos, o a mediana pode não ser determinada de forma única: para dados numéricos, a meia soma de dois valores adjacentes é mais frequentemente usada (ou seja, a mediana do conjunto (1, 3, 5, 7) é considerada igual a 4), para mais detalhes veja.

A mediana também pode ser definida para variáveis aleatórias: neste caso, divide a distribuição pela metade. Grosso modo, a mediana de uma variável aleatória é um número tal que a probabilidade de obter o valor da variável aleatória à direita dela é igual à probabilidade de obter o valor à esquerda dela (e ambos são iguais a 1/2); Para uma definição mais precisa, consulte .

A mediana também pode ser considerada o percentil 50, o quantil 0,5 ou o segundo quartil de uma amostra ou distribuição.

Propriedades da mediana para variáveis aleatórias

F(x) = 0,5 (\estilo de exibição F(x)=0,5)

Se a distribuição for uma função contínua estritamente crescente, então a solução da equação é única. Se a distribuição apresentar descontinuidades, então a mediana pode coincidir com o valor mínimo ou máximo (extremo) possível da variável aleatória, o que contradiz o entendimento “geométrico” deste termo.

A mediana é uma característica importante da distribuição de uma variável aleatória e, assim como o valor esperado, pode ser usada para centralizar a distribuição. Como as estimativas da mediana são mais robustas, a sua estimativa pode ser mais preferível para distribuições com as chamadas. caudas pesadas. Contudo, as vantagens de estimar a mediana em comparação com a expectativa matemática só podem ser discutidas se estas características da distribuição coincidirem, em particular, para funções de densidade de probabilidade simétricas.

A mediana é determinada para todas as distribuições e, em caso de ambigüidade, é naturalmente definida posteriormente, enquanto a expectativa matemática pode não ser determinada (por exemplo, para a distribuição de Cauchy).

Exemplo de uso

Suponha que houvesse 19 pessoas pobres e um milionário numa sala. Cada pessoa pobre tem 5 dólares e cada milionário tem 1 milhão de dólares (10 6). O total é de US$ 1.000.095. Se dividirmos o dinheiro igualmente entre 20 pessoas, obteremos US$ 50.004,75. Esta será a média aritmética da quantidade de dinheiro que todas as 20 pessoas nesta sala tinham.

A mediana, neste caso, será igual a $ 5 (metade da soma do décimo e do décimo primeiro, mediana valores da série classificada). Isso pode ser interpretado da seguinte maneira. Tendo dividido a nossa empresa em dois grupos iguais de 10 pessoas, podemos dizer que no primeiro grupo todos não têm mais de 5 dólares, e no segundo não menos de 5 dólares. Em geral, podemos dizer que a mediana é quanto a pessoa “média” trouxe consigo. Pelo contrário, a média aritmética é uma característica inadequada, uma vez que excede significativamente a quantidade de dinheiro disponível para a pessoa média.