MA. Повърхностни интеграли от втори род
Теоретичен минимумТази тема продължава обсъждането на криволинейни и повърхностни интеграли, започнало в темата "". Препоръчително е да се запознаете с тази тема предварително. Поради по-голямата сложност на темата, криволинейни и повърхностни интеграли
вторият вид се разглеждат отделно. Тук се обсъждат повърхностни интеграли от втори вид - може би най-сложната интегрална операция в
анализ на функции на много променливи. Планът ще бъде напълно подобен на разглеждането на криволинейния интеграл от втори род. Да започнем с физически приложения,
и след това ще преминем към формалния математически аспект.1. Физически приложения на повърхностния интеграл от втори род
Най-естественият начин за въвеждане на повърхностен интеграл от втори вид е да се разгледа потокът на течност през някаква повърхност. Нека започнем с един прост случай:
течността тече по оста x с постоянна скорост. Нека изберем област, перпендикулярна на потока, и намерим масата на течността, преминаваща през нея
нея навреме. През това време се образува "паралелепипед" с височина и основна площ от. Масата на този "паралелепипед"
равна на, където е плътността на течността.
Сега оставете течността да тече успоредно на равнината под ъгъл спрямо оста x, но все пак със скорост. Сайтът от предишния
случай все пак ще го поставим перпендикулярно на абсцисната ос. С течение на времето през него преминава наклонен „паралелепипед“ (виж фиг. 1). Масата му
равна на . Имайте предвид, че въвеждането на единичен нормален вектор в сайта ни позволява да пишем.
Въвежда се формален вектор на елементарна площ, чийто модул е равен на , а посоката му съвпада с посоката на вектора
нормално за сайта. Тогава. Тази нотация ви позволява да не се притеснявате за посоката на вектора на скоростта на течността по отношение на
към сайта.Остава да се изостави малката площ, през която тече течността, и допускането на постоянен модул и посока на скоростта. Тогава
повърхността е разделена на малки части, в рамките на които векторът на скоростта може да се счита за постоянен. Масата на течността, преминаваща през повърхността, е
се дава приблизително от сумата.
Точната формула ще бъде получена в границата на разделянето на повърхността на безкрайно малки части. Границата е повърхностен интеграл от втори вид:.
При написването на този раздел е използван фрагмент от учебен материал от преподавател от катедрата по обща физика, използван от него в семинарните занятия.2. Определение на повърхностен интеграл от втори род
Сега относно формалната конструкция на интеграла. Поради факта, че векторното поле е интегрирано върху повърхността, има смисъл да се изясни от коя страна
повърхност, интегралът се изчислява (както при изчисляване на потока на течност: течността се влива в повърхността или изтича от нея). Затова е специално уточнено
че повърхността, върху която се извършва интегрирането, трябва да бъде двустранна или ориентировъчна (т.е. лентата на Мьобиус като цяло няма да работи). Повърхност
непосредствено ориентирани, т.е. избрана е определена посока на нормалата към повърхността (например, ако интегралът се изчислява върху сфера, тогава нормалата може да бъде
насочени от сферата или в сферата). Компонентите на полето в общия случай са функции на точка. Повърхност на интеграция
се разделя на малки части, избира се точка във всяка част и се съставя сумата
,
където е площта на проекцията на елемента върху равнината, е площта на проекцията на този елемент върху равнината, е площта
проекция на този елемент върху равнина. Извършваме сумирането върху всички елементи, на които е разделена повърхността:
и отидете до границата, насочвайки диаметъра на най-голямата частична област към нула. Границата е повърхностен интеграл от втори род
.
Нека покажем как да редуцираме този интеграл до формата от стъпка 1. За да направите това, ще трябва да направите малко отклонение от чисто геометричен характер. Нека има
равнина, пресичаща координатните оси (виж фиг. 2). Частта от тази равнина, разположена в първия октант, има площ от. Трябва да намерите района
и трите ортогонални проекции на дадена част от равнината върху координатни равнини. Както е известно, площта на проекцията на фигура е равна на произведението на площта
самата фигура и косинуса на ъгъла между равнината на фигурата и равнината, върху която се проектира (виж фиг. 3). Тези. трябва да намерите ъглите, които правят
равнина с координатни равнини. Ъгълът между две равнини е равен на ъгъла между техните нормали. Нормалната единица към равнината има компоненти,
които са неговите насочващи косинуси. Следователно ъгълът между равнината и равнината е равен (виж фиг. 2) и следователно .
Същата връзка ще бъде валидна за безкрайно малки области: . И по подобен начин.
Като се вземат предвид тези отношения, интегралът приема формата
.
Между другото, тази форма на запис е по-визуална, така че ще работим с нея.Обръщането на посоката на нормалата кара интеграла да промени знака.
3. Изчисляване на повърхностен интеграл от втори род
След редуциране на интеграла до форма, съдържаща направлението косинуси на нормалата към повърхността, проблемът по същество се свежда до записване на нормалната единица
с по-нататъшно изчисляване на повърхностния интеграл от първи род. Има някои специфики в тези действия, така че нека разгледаме изчислението в детайли
интеграли от този тип.Нека започнем със случая, когато интеграционната повърхност е дадена чрез явно уравнение, например,
. Тогава нормалният вектор се записва по следния начин:
,
и елемента на повърхността.
В резултат на това повърхностният интеграл приема следната форма:
, (1)
където е областта на равнината, в която се проектира интеграционната повърхност.Възможно е повърхността на интегриране да е правилно проектирана върху равнината (и дадена от уравнението) или върху равнината
(и се дава от уравнението). След това формулата, по която се изчислява интегралът, се коригира леко:
(2)
или
. (3)
Разбира се, не се препоръчва да запомняте такива формули: лесно е да объркате нещо - по-добре е да ги възстановите във връзка с конкретен
изчисление отново въз основа на формулата за нормалния вектор и площта на малък повърхностен елемент.Има един подчертан случай, когато повърхността е правилно проектирана върху трите координатни равнини, т.е. от уравнението на повърхността всяка променлива
може да се изрази недвусмислено. Тогава изчислението е значително опростено. Обърнете внимание на структурата на формули (1) - (3). Във всяка от тях има по три
термини и един от тях изглежда по-прост от останалите. Когато се проектира повърхност върху равнина, този термин съдържа компонента
полета ; когато се проектира върху равнина, това е терминът, съдържащ компонента; когато се проектира върху равнина, това е терминът
съдържащ компонент. Ако повърхността се проектира правилно върху която и да е координатна равнина, тогава разделяме интеграла
на три части и проектирайте всяка част по най-удобния начин:
.И накрая, случаят на параметрично дефиниране на повърхността
.
Както при изчисляването на повърхностния интеграл от първи вид, трябва да се вземат предвид три якобиани:
.
Чрез тях се изразяват насочващите косинуси на нормалата:
,
повърхностен елемент
.
Така за интеграла получаваме
,
където е обхватът на промените на параметрите, съответстващи на интеграционната повърхност.4. Формула на Стокс. Формула на Остроградски-Гаус
Повърхностният интеграл от втори вид е свързан с две формули, които намират различни приложения, включително във физически приложения.
Формула на Стокс:
,
Където ,
повърхността е опъната върху контура, преминаването на контура е в съответствие с избора на нормалата към повърхността съгласно правилото на десния винт.
Необходими са пояснения, ако интеграционната повърхност има „дупки“.
Формулата на Грийн е частен случай на тази формула. Освен това от формулата на Стокс следва условието за независимост на криволинейния интеграл на втория
вид от формата на пътя.Формула на Остроградски-Гаус.
За векторно полеформулата е изпълнена
където повърхността ограничава обема.Формулата на Остроградски-Гаус има различни приложения. Нека разгледаме две от тях. Първо, лесно е да се докаже, че обемът на тялото може да бъде изчислен
според формулатаВторо, понякога е необходимо да се изчисли повърхностен интеграл от втори вид върху отворена повърхност, което включва тромави изчисления.
След това повърхността се затваря, интегралът се преобразува в троен и интегралът върху добавената повърхност се изважда (вижте примера по-долу).Забележка. Формулите на Стокс и Остроградски-Гаус се записват по-удобно във векторен анализ, като се използва извивката и дивергенцията на векторното поле.
Примери за изчисляване на повърхностни интеграли от втори род
Пример 1. Равнинен интеграл.. Тогава получаваме) части от елиптичен параболоид (външна нормала).
Нека пренапишем интеграла във формата
.
Интеграционната повърхност - елиптичен параболоид - се проектира правилно само върху равнината, така че записваме уравнението на повърхността във формата
.
Намерете единичния нормален вектор:.
Концепцията за двоен интеграл върху плоска област може лесно да се обобщи за случая на интегриране върху повърхност. Нека (S) е повърхност (затворена или отворена) и непрекъсната функция на точка от тази повърхност. Разбийте (S) на части
и нека площите на тези части и всякакви точки, разположени върху тези части. Съставяне на сбора от произведенията
Границата на тази сума с безкрайно нарастване на броя на деленията и безкрайно намаляване на всяка от частите се нарича интеграл на функцията върху повърхността
Да приемем, че прави линии, успоредни на оста Z, пресичат повърхността само в една точка (фиг. 48) и нека проекцията (S) е върху равнината XOY. Използвайки формула (26), която установява връзката между елементарната повърхност (S) и съответната площ на нейната проекция, можем да намалим интеграла върху повърхността (S) до интеграла върху плоската площ:
в този случай се приема, че тя е различна от нула и че стойността на функцията в точка N от областта съвпада със стойността на функцията, определена върху повърхността в тази точка M, чиято проекция съвпада с . Ако уравнението на повърхността (S) е дадено в ясна форма (22) и функцията е изразена чрез координати, тогава при интегриране върху нея е достатъчно функцията да бъде заменена в израза. Знаменателят от дясната страна на (29) се определя от третата от формули (24).
Обърнете внимание, че повърхностните интеграли очевидно притежават всички свойства на двоен интеграл, посочени в , по-специално теоремата за средната стойност е валидна за тях.
Нека сега докажем една от основните формули в теорията на множествените интеграли - формулата на Остроградски, която установява връзка между тройния интеграл върху обем и интеграла върху повърхността (S), която ограничава този обем. Ще разгледаме как и къде се пресичат прави линии, успоредни на оста Z (S) в не повече от две
точки. Нека запазим същата нотация като на фиг. 40. Нека да разгледаме и посоката на нормалата към (S), като ще приемем, че тя е насочена извън обема (V) (външна нормала) (фиг. 50). Тази посока образува остър ъгъл с оста OZ в горната част на повърхността (I) и тъп ъгъл в долната част (I). Следователно в долната част отбелязваме, че на линията на контакт на повърхността (5) с издадения цилиндър (фиг. 50). Формула (26) дава
Нека, заедно с производната, е непрекъснато в областта до (S). Нека разгледаме тройния интеграл на функцията Използвайки формула (16), ще имаме
Но интегралът на производната е равен на разликата между стойностите на антипроизводната функция при горната и долната граница:
Заменяйки с по формули (30), свеждаме интегрирането до интегриране по (S), а в първия интеграл, съдържащ променливата ордината на част (I) от повърхността (S), ще трябва да използваме първата от формулите (30) и получаваме интеграла върху (II), във втория интеграл, съдържащ ще трябва да използвате втората от формулите (30), и получавате интеграла върху (I):
Символите за z вече не могат да се изписват, тъй като е посочено върху коя част от повърхността се извършва интегрирането. От дясната страна е сумата от интегралите по части (II) и (I), т.е. интегралът по цялата
повърхности (S):
Ако са функции, които имат свойствата на функция R, тогава, като се има предвид това
Въз основа на (31) можем да напишем формулата за интегриране по части:
По абсолютно същия начин, като вземем две други функции, които можем да докажем
Събирайки получените три формули термин по термин, стигаме до формулата на Остроградски
Подобно на (31,), се записват формули за интегриране по части за производни по x и y.
За краткост тук не пишем аргументите x, y, z на функциите P, Q, но трябва да помним, че това са функции, дефинирани в обем и непрекъснати с техните производни.
В следващата глава ще дадем голям брой примери за прилагането на формулата на Остроградски.
Количествата са функции, дефинирани на повърхността (S). Считахме ги за непрекъснати. Може да се направи по-общо предположение, а именно да приемем, че (S) е разделена на краен брой части, на всяка от които посочените функции са непрекъснати. Такъв ще бъде случаят, например, ако (S) е полиедър.
При извеждането на формула (31) приехме, че прави линии, успоредни на оста, пресичат повърхността (S) на областта в не повече от две точки. Не е трудно тази формула да се обобщи към области от по-обща форма. Нека отбележим първо, че ако повърхността (S), в допълнение към горната част (II) и долната част (I), има цилиндрична странична част с образуващи, успоредни на оста, тогава върху тази странична част и добавяне тази част от дясната страна на формула (31) не променя стойността на повърхностния интеграл, така че цялото доказателство на формулата остава валидно. В по-общ случай е достатъчно да се използват цилиндрични повърхности с образуващи, успоредни на оста, за да се разделят на краен брой части, които отговарят на предходните условия, и да се приложи формула (31) към всяка част. Събирайки така получените формули, ще имаме от лявата страна троен интеграл по целия обем. От дясната страна ще имаме сумата от интегралите върху всички повърхности на онези части, на които сме разделили (v). Интегралите върху намалените помощни цилиндрични повърхнини, както е посочено по-горе, са равни на нула. Така, в резултат на добавяне от дясната страна, ще имаме интеграл върху повърхността (S) на оригиналния обем. И така, формула (31) се оказва валидна за области от по-общ вид.
Нека разгледаме интегралите на функциите, дефинирани върху повърхности, така наречените повърхностни интеграли.Теорията на повърхностните интеграли е в много отношения подобна на теорията на криволинейните интеграли. Има повърхностни интеграли на първия и
от втория вид.
4.1. Повърхностни интеграли от първи тип. Нека функцията f(x, y, z)
дефинирана върху късово гладка повърхност S, ограничена от кусочно гладък контур (фиг. 4.1). Нека го разбием
съответно ∆ s 1, ∆ s 2 ..., ∆ s n. Вземайки произволна точка M i (x i, y i, z i) във всяка част S i, i = 1, n, изчисляваме стойността на функцията в нея и правим следната сума:
σ n= ∑ f (x i, y i, z i) ∆ s i | |||||
i= 1 | за функцията f (x, y, z) от |
||||
който се нарича интеграл | |||||
повърхност S. | |||||
Последната граница I на това | докато се стремим | ||||
най-големият λ от диаметрите на всички частични повърхности S i | |||||
1, н |
|||||
ако съществува и не зависи нито от метода за разделяне на повърхността на частични, нито от избора на точки, тогава се нарича повърхностен интеграл от първи тип (върху повърхността)от функция
f (x, y, z) по повърхността S и се обозначава със символа | ∫∫ f(x, y, z) ds. |
|
И така, по дефиниция | ||
= ∫∫ f(x, y, z) ds. | ||
I = lim ∑ f(xi , yi , zi ) ∆ si | ||
λ → 0i = 1 | ||
Повърхностният интеграл от първи тип е обобщение на двойния интеграл, следователно условията за съществуването на двойния интеграл и неговите свойства лесно се пренасят върху повърхностния интеграл от първи тип.
Изчисляване на повърхностни интеграли от първи тип свежда до изчисляване на двойни интеграли: въз основа на уравнението на повърхносттаС,
интеграндът се трансформира в две променливи, чийто диапазон ще бъде проекцията на повърхността S върху координатната равнина, съответстваща на тези променливи.
Нека повърхността S е дефинирана от уравнението z = z (x, y) и z (x, y) е непрекъсната заедно с нейните частни производни z ′ x, z ′ y в затворена област S xy, която е проекцията на повърхността S върху координатната равнина xOy, тогава
∫∫ f(x, y, z) ds= ∫∫ f(x, y, z(x, y)) 1 + (z′ x ) 2 + (z′ y ) dxdy. | ||
S xy | ||
Тази формула изразява повърхностния интеграл от първи тип чрез двойния интеграл върху проекцията на повърхността S върху координатната равнина xOy.
Повърхностните интеграли от първи тип върху повърхността S се изчисляват по подобен начин чрез двойни интеграли върху нейните проекции върху
координатни равнини xOz и yOz съответно: | |||
∫∫ f (x,y,z)ds = ∫∫ f (x,y (x,z),z) | 1+ (y ′ x )2 + (y ′ z )dxdz , | ||
S xz | |||
∫∫ f (x, y,z)ds= ∫∫ f (x(y,z), y,z) | 1 + (x′ y )2 + (x′ z )dydz. | ||
S yz | |||
Използвайки повърхностни интеграли от първия тип, е възможно да се изчисли площта на повърхността, както и масата, статични моменти, моменти на инерция и координати на центъра на масата за материални повърхности с известна плътност на разпределение на повърхностната маса.
Пример 4.1. Изчисли
∫∫ 1 + 4 x 2 + 4 y 2 ds , където S е част от парабо-
сила на въртене z = 1 − x 2 − y 2 , отсечена от равнината z = 0 .
Решение. Нека проектираме повърхността
S към равнина xOy.
Проекцията S xy е окръжност, ограничена от окръжността x 2 + y 2 = 1 (фиг.
4.2). Ще изчислим дадения повърхностен интеграл с помощта на формула (4.2), за която намираме z ′ x = − 2 x , z ′ y = − 2 y . След това, ангажиране на двойно
интегрална | към полярния | координати, | S xy е кръг, |
||||||||
1 +4 x 2 +4 y 2 ds =∫∫ | 1+ 4x 2 + 4y 2 | 1 + 4 x2 + 4 y2 dxdy= |
|||||||||
S xy | |||||||||||
= ∫∫ (1 +4 x 2 +4 y 2 ) dxdy = | |||||||||||
S xy | |||||||||||
= ∫ d ϕ ∫ (1 +4 ρ 2 ) ρ d ρ =∫ | + ρ 4) | d ϕ= | ∫d ϕ . |
||||||||
4.2. Двустранни повърхности. Повърхнината S се нарича
двустранно, ако преминаването по който и да е затворен контур, разположен върху повърхността S и не пресича нейните граници, при връщане към началната точка не променя посоката на нормалата към повърхността. В противен случай повърхността се нарича едностранна. Примери за двустранни повърхности: равнина, сфера и всяка повърхност, дефинирана от уравнението z = z (x, y), където z = z (x, y), z ′ x (x, y), z ′ y (x , y) - непрекъснато в някаква областG. Пример за едностранна повърхност е лентата на Мьобиус.
4.3. Повърхнинен интеграл от втори тип. Нека да - гладка повърхност, дадена от уравнението z = z(x, y) и функция f(x, y, z)
определени в точки от повърхността S.
Нека изберем една от страните на повърхността, тоест една от двете възможни посоки на нормалата в точки от повърхността (така сме ориентирали повърхността). Ако нормалите образуват остри ъгли с
ос Oz , тогава ще говорим загорната страна на повърхността (относно положителната посока на нормалата ), и ако нормалните са –тъпи ъгли с оста Oz, тогава говорим за долната страна на повърхността (отрицателната посока на нормалата).
Нека разделим повърхността S произволно на n части S 1, S 2 ..., S n и чрез (S xy ) i означим проекцията на i-тата част от повърхността
към равнината xOy. Във всяка частична повърхност S i, i = 1, n, изберете произволна точка M i (x i, y i, z i) и изчислете стойността на функцията
в него ще направим сумата
σ n= ∑ f (x i, y i, z i) ∆ s i, i = 1
където ∆ s i - площ (S xy) i, взета със знак плюс, ако е избрана горната страна на повърхността S, и със знак минус, ако е избрана долната страна
повърхност S. Тази сумаσ n се нарича интегрална сумаза функцията f(x, y, z).
Крайната граница I на интегралната сума, тъй като най-големият λ от всички диаметри на проекцията (S xy ) i клони към нула, ако съществува и
не зависи нито от метода на разделяне на повърхността S, нито от избора на точки
M i (x i, y i, z i), тогава тази граница се нарича повърхностен интеграл на втория тип функция f(x, y, z) по протежение на избраната страна на повърхността чрез променливи x и y и се означава с ∫∫ f (x, y, z) dxdy. Така според
определение
повърхност S в променливи x и y.
По подобен начин можете да дефинирате повърхностни интеграли от втори тип върху избрана страна на повърхността S в променливи y и z, в променливи x и z:
∫∫ f(x, y, z) dydz, | ∫∫ f(x, y, z) dxdz. |
Нека P (x, y, z), Q (x, y, z), R (x, y, z) са функции, интегрируеми върху
повърхност S в променливите y и z, x и z, x и y, съответно. Сума от интеграли
∫∫ P(x, y, z) dydz, | ∫∫ Q(x, y, z) dxdz, | ∫∫ R(x, y, z) dxdy | |
се нарича общ интеграл от втори тип и се обозначава | |||
∫∫ P(x, y, z) dydz+ Q(x, y, z) dxdz+ R(x, y, z) dxdy. | |||
Тъй като считаме повърхността S за двустранна и интегралът се простира до определена страна от нея, тогава когато страната на интеграционната повърхност се промени, повърхностният интеграл от втория тип променя знака на противоположния– това е разликата му от повърхностния интеграл от първия тип.
Изчисляване на повърхностни интеграли от втори тип се свежда до изчисляване на двойни интеграли.
Нека една ориентирана (изберете горната страна) гладка повърхност S е дадена от уравнението z = z (x, y), където z (x, y) е непрекъсната в
затворена площ S xy - проекция на повърхността S върху равнината xOy; функцията f(x, y, z) е непрекъсната върху S. Тогава формулата е валидна
∫∫ f(x, y, z) dxdy= ∫∫ f(x, y, z(x, y)) dxdy, | ||||
S xy | ||||
изразяващ повърхностния интеграл от втори тип върху променливите x и | ||||
чрез двойно. Ако изберем долната страна на повърхността S, тогава отпред |
||||
интеграл, от дясната страна ще се появи знак минус. | ||||
Формулите са валидни по същия начин | ||||
∫∫ f(x, y, z) dydz= ∫∫ f(x(y, z), y, z) dydz, | ||||
S yz | ||||
∫∫ f(x, y, z) dxdz= ∫∫ f(x, y(x, z), z) dxdz, | ||||
S xz | ||||
където повърхността S | според уравненията | x = x(y, z) | ||
y = y(x, z) и Syz | и S xz - | проекции на повърхността S, съответно | ||
равнини yOz и xOz.
За изчисляване на интеграла на общата форма (4.6) се използват формули (4.7)–(4.9), ако повърхността S е проектирана еднозначно върху всички
координатни равнини. В по-сложни случаи повърхността S се разделя на части, които имат посочените свойства, а общият интеграл се представя под формата на интеграли върху тези части.
Пример 4.2. Пресметнете
∫∫ (y 2 + z 2 ) dxdy, където S е горната страна
повърхност z = | 1 − x 2 | Изрязан плосък |
||||||||
зарове y = 0, y = 1. | ||||||||||
Решение. Уравнението x 2 + z 2 = 1 - |
||||||||||
посочен е кръгов цилиндър с генератора, |
||||||||||
успоредна на оста Oy и равнината y = 0 и |
||||||||||
y = 1 | паралелен | координирам |
||||||||
равнина xOz (фиг. | Проекция |
|||||||||
повърхност S на равнината xOy е |
||||||||||
правоъгълник S xy, определен от неравенствата − 1 ≤ x ≤ 1, | 0 ≤ y ≤ 1. |
|||||||||
Тогава по формула (4.7) имаме | ||||||||||
∫∫ (y2 + z2 ) dxdy= ∫∫ (y2 + (1 − x2 )) dxdy= ∫ dx∫ (y2 − x2 + 1) dy= |
||||||||||
S xy | −1 | |||||||||
+ (1− x 2 )y ) | ||||||||||
= ∫ dx ( | ||||||||||
−1 | ||||||||||
− x2 ) dx | ||||||||||||||||||||||||||||||
= ∫ ( | ||||||||||||||||||||||||||||||
−1 | −1 | |||||||||||||||||||||||||||||
Пример 4.3. Изчисли | ||||||||||||||||||||||||||||||
∫∫ xdydz+ ydxdz+ zdxdy, където S е горната | ||||||||||||||||||||||||||||||
страна на част от равнината x + z − 1 = 0 | ||||||||||||||||||||||||||||||
отрязани от равнини y = 0, y = 4 и | ||||||||||||||||||||||||||||||
разположен в първия октант (фиг. 4.4). | ||||||||||||||||||||||||||||||
Решение. Проекция на повърхност S върху | ||||||||||||||||||||||||||||||
равнината xOy е правоъгълникът S xy, | ||||||||||||||||||||||||||||||
определени от неравенствата 0 ≤ x ≤ 1, | ||||||||||||||||||||||||||||||
0 ≤ y ≤ 4 . Проекция на повърхност S върху | ||||||||||||||||||||||||||||||
равнината yOz е правоъгълник | S yz, определени от неравенствата |
|||||||||||||||||||||||||||||
0 ≤ z ≤ 1,0 ≤ y ≤ 4. Тъй като равнината S е перпендикулярна на равнината |
||||||||||||||||||||||||||||||
xOz , тогава ∫∫ ydxdz = 0. Тогава по формули (4.7) и (4.9) имаме |
||||||||||||||||||||||||||||||
∫∫ xdydz+ ydxdz+ zdxdy= ∫∫ (1 − z) dydz+ |
||||||||||||||||||||||||||||||
S yz | ||||||||||||||||||||||||||||||
+ ∫∫ (1 − x) dxdy= ∫ dy∫ (1 − z) dz+ ∫ dy∫ (1 − x) dx= |
||||||||||||||||||||||||||||||
S xy | ||||||||||||||||||||||||||||||
− z ) | (1− x) | |||||||||||||||||||||||||||||
2 ∫ | dy = 4. |
|||||||||||||||||||||||||||||
= ∫ dy − | + ∫ dy − | |||||||||||||||||||||||||||||
4.4. Формула на Остроградски. Формулата на Остроградски установява връзка между повърхностния интеграл върху затворена повърхност и тройния интеграл върху пространствената област, ограничена от тази повърхност.
Нека V е правилна затворена област, ограничена от повърхността S, и нека функциите P(x, y, z), Q(x, y, z), R(x, y, z)
са непрекъснати заедно с техните частни производни от първи ред в даден регион. Тогава важи следната формула:
∫∫∫( | ∂P | ∂Q | ∂ R ) dxdydz= ∫∫ Pdydz+ Qdxdz+ Rdxdy, (4.10) |
|||
∂x | ∂г | ∂z | ||||
НареченФормулата на Остроградски 1 .
С помощта на формулата на Остроградски е удобно да се изчисляват повърхностни интеграли върху затворени повърхности.
Пример 4.4.Използвайки формулата на Остроградски, изчислете
∫∫ xdydz + ydxdz + zdxdy , | Където С | ||||||||||||||||||||||||||
страна на пирамидата | ограничен | самолети | |||||||||||||||||||||||||
х + г + z = 1, | х= 0,г= 0, | z= 0 (фиг. 4.5). | |||||||||||||||||||||||||
Според | |||||||||||||||||||||||||||
Остроградски: | |||||||||||||||||||||||||||
П(х,г,z)= х,Q(х,г,z)= г,Р(х,г,z)= z. | |||||||||||||||||||||||||||
Тогава: ∂ П+ | ∂ Q+ | ∂Р | = 1+ 1+ 1= 3,и намираме | ||||||||||||||||||||||||
∂х | ∂г | ∂z | |||||||||||||||||||||||||
1− х | 1 −х−г | ||||||||||||||||||||||||||
∫∫ xdydz + ydxdz + zdxdy = 3 ∫∫∫ dxdydz = 3 ∫ dx ∫ dy | ∫ дз = | ||||||||||||||||||||||||||
1− х | 1 −х−г | 1− х | |||||||||||||||||||||||||
= 3 ∫ dx ∫ dy ∫ дз = 3 ∫ dx ∫ (1 − х − г ) dy = | |||||||||||||||||||||||||||
г 2 | 1− х | ||||||||||||||||||||||||||
3 ∫ dx (г − xy − | |||||||||||||||||||||||||||
−2 х+1 | 3 (х− 1) | ||||||||||||||||||||||||||
= 3 ∫ (1 −х−х+х2 − | ) dx = | ∫ (х − 1) 2 dx = | |||||||||||||||||||||||||
Забележка 4.1.Връзката между повърхностните интеграли от първи и втори тип е подобна на връзката между криволинейни интеграли:
∫∫ f (х , г , z ) dxdy = ∫∫ f (х , г , z )cosα ds ,
∫∫ f (х , г , z ) dydz = ∫∫ f (х , г , z )cosβ ds ,
∫∫ f (х , г , z ) dxdz = ∫∫ f (х , г , z )cosγ ds ,
Където cosα ,cosβ ,cosγ - посока косинуси на нормалата, съответстваща на
избраната страна на повърхността. ,г) | непрекъснато в областта Сxy– повърхностни проекции С |
||||||||||||||||||||||
до самолета xOy;Л | – контур, | ограничаване | повърхност | С ; л – |
|||||||||||||||||||
проекция на пространствена линия Лдо самолета | xOy , | същество |
|||||||||||||||||||||
развъдник, ограничаващ района д. Нека изберем горната страна |
|||||||||||||||||||||||
повърхности С. Ако функциите П(х, г, z), Q(х, г, z), Р(х, г, z) | непрекъснато |
||||||||||||||||||||||
заедно с неговите частни производни от първи ред на |
|||||||||||||||||||||||
повърхности С, тогава е валидна следната формула: | |||||||||||||||||||||||
∫ Pdx + Qdy + Rdz = | |||||||||||||||||||||||
= ∫∫ | (∂ Q | ∂ П) dxdy + ( | ∂Р | ∂ Q) dydz + (∂ П | ∂ Р) dxdz | ||||||||||||||||||
∂х | ∂г | ∂г | ∂z | ∂z | ∂х | ||||||||||||||||||
(Л- се движи в положителна посока) | Наречен формула |
||||||||||||||||||||||
Ако като повърхност Свземете площ дна повърхността xOy |
|||||||||||||||||||||||
(z= 0 ), то от (4.11) получаваме формулата на Грийн | ∂Q | ∂ П) dxdy . | |||||||||||||||||||||
∫ П (х , г ) dx + Q (х , г ) dy = ∫∫ ( | |||||||||||||||||||||||
∂х | ∂г | ||||||||||||||||||||||
Така формулата на Грийн е частен случай на формулата на Стокс. |
|||||||||||||||||||||||
Имайте предвид, че повърхностният интеграл от втория тип във формулата |
|||||||||||||||||||||||
Стокс (4.11) може да бъде заменен с повърхностния интеграл на първия |
|||||||||||||||||||||||
Тип. Тогава тази формула ще приеме формата | |||||||||||||||||||||||
∫ Pdx + Qdy + Rdz = | |||||||||||||||||||||||
∂Q | ∂П | ∂Р | ∂Q | ∂П | ∂Р | ||||||||||||||||||
= ∫∫ | )cos α + ( | )cos β + ( | )cos γ | ||||||||||||||||||||
∂х | ∂г | ∂г | ∂z | ∂z | ∂х | ds , | |||||||||||||||||
Където cos α ,защото β ,защото γ , | означава | водачи | косинуси | ||||||||||||||||||||
съответстващи на избраната страна на повърхността. | |||||||||||||||||||||||
използвайки формулата | изчисли |
||||||||||||||||||||||
∫ х 2 г 3 dx + dy + здз , | кръг, | дадени от уравненията |
|||||||||||||||||||||
х 2 + г 2 + 1, z = 0 . | Повърхност Сслужи горната страна на полусферата |
||||||||||||||||||||||
х 2+ г 2+ z 2= 1, | z> 0 (Лвърви в положителна посока). |
||||||||||||||||||||||
За случаите, когато интегрирането се извършва не върху сегмент от крива, а върху ограничена повърхност. Подобно на криволинейните интеграли, повърхностните интеграли са от първи и втори вид.
Повърхнинен интеграл от първи род написана във формуляра
Където f(М) = f(x,y,z) е функция на три променливи и повърхността σ - област на интегриране на тази функция. Ако f(x,y,z) е равно на единица, тогава повърхностният интеграл е равен на площта на повърхността.
Представете си доста голям слънчоглед с много, много малки семена. След това, от сумата от повърхностите на много, много малки семена, разположени на повърхността на слънчогледа, може да се изчисли повърхността на слънчогледа - това може да е опростена интерпретация на повърхностния интеграл. Защо така?
Нека преминем към по-формална дефиниция на повърхностен интеграл. Повърхност σ разделена на нчасти с площи Δ σ 1 , Δ σ 2 , ..., Δ σ н. Ако изберете произволна точка на всяка частична повърхност (семе) Мазс координати ( ζ аз, η аз, ς аз,), тогава можем да обобщим
Тази сума се нарича интегрална сума за функцията f(М) на повърхността σ . Сега ще увеличим максимално броя на такива малки части и най-големия диаметър Δ σ аз- напротив, намалете. Ако интегралната сума като най-голям от диаметрите на частите клони към нула (тоест, както вече отбелязахме, всички части са много малки) има граница, тогава тази граница се нарича повърхностен интеграл от първи род от функция f(М) на повърхността σ .
Изчисляване на повърхностен интеграл от първи род
Нека повърхността σ дадено от уравнението z = z(х, г) , неговата проекция върху равнината xOyе площта дxy, докато функцията z = z(х, г) и неговите частни производни са непрекъснати в региона дxy.
Пример 1.
Където σ - част от равнината в първи октант.
Решение. Чертеж:
От уравнението на равнината получаваме израза "zet": 
.
Тогава частните производни са: , и
.
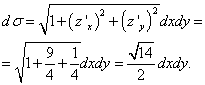Повърхност σ е триъгълникът, показан на чертежа ABC, и неговата проекция върху равнината xOy- триъгълник AOB, която е ограничена от прави линии х = 0 , г= 0 и 3 х + г= 6. Нека преминем от повърхностния интеграл към двойния интеграл и да го решим:
.
Концепцията за повърхностен интеграл от втори род
Преди да преминете към дефиницията на повърхностен интеграл от втори род, е необходимо да се запознаете с понятията страни на повърхности и ориентирани повърхности.
Нека в пространството е дадена гладка повърхност σ . Нека изберем произволна точка на тази повърхност Ми начертайте нормалния вектор към повърхността през него. През точката Мще извършим и на повърхността σ произволен контур, който няма общи точки с границата на повърхността σ . Точка Мзаедно с нормалния вектор ще се движим по контура, така че нормалният вектор да е постоянно перпендикулярен на повърхността σ . При връщане на точката Мдо началната позиция са възможни два случая: посоката на нормалния вектор ще остане същата или ще се промени на противоположната.
Ако посоката на нормалния вектор не се промени, тогава повърхността σ наречена двустранна. Ако при преминаване на контура посоката на нормалния вектор се промени на противоположната, тогава повърхността се нарича едностранна. Двустранните повърхности се наричат ориентирани повърхности, едностранните повърхности се наричат неориентирани повърхности.
Пример за едностранна повърхност е лента на Мьобиус (на снимката по-горе), която може да бъде направена от лента хартия с една страна, завъртяна на 180 градуса и след това краищата да бъдат залепени заедно. И ето какво е важно тук: за едностранна повърхност не се въвежда понятието повърхностен интеграл от втори род .
Така че ще разгледаме само двустранни повърхности. Примери за двустранни повърхности са равнини, сфери, елипсоиди и параболоиди.
Положителната страна на двустранна повърхност определя посоката на нормалния вектор. Противоположната страна на повърхността се нарича отрицателна. Положителната страна на повърхността е нейната горна страна. Ако единичните нормални вектори сключват остри ъгли с оста Оз, тогава се избира горната страна на повърхността z = z(х, г) , ако ъглите са тъпи, тогава долната страна на повърхността.
Както в случая с повърхностния интеграл от първи вид, повърхността може да бъде разделена на нчасти. При формулирането на концепцията за повърхностен интеграл от първи вид интегралната сума включва площите на всяка от частите, по които се умножават стойностите на функцията f(Ми). В случай на повърхностен интеграл от втори род не се вземат площите на самите части, а площите на техните проекции върху координатни равнини . И за да разграничим функцията на три променливи от интеграл от първи вид, ние означаваме Р(х,г,z) . Тогава интегралната сума ще бъде записана по следния начин:
,
където Δ саз- площите на споменатите проекции на части от страната на повърхността върху координатната ос (засега ще приемем, че на оста xOy).
С такива конвенции и означения дефиницията на повърхностен интеграл от втори род е подобна на дефиницията на интеграл от първи вид. А именно: повърхностен интеграл от втори род е границата на дадена интегрална сума, тъй като най-големият диаметър на частите от разглежданата повърхност клони към нула.
Написано е така:
.
В този случай функцията Р(х,г,z) интегрируеми върху променливи хИ г, тъй като части от повърхността са проектирани върху равнината xOy.
По подобен начин можем да напишем два други повърхностни интеграла от втори вид:
(функция П(х,г,z) интегрируеми върху променливи гИ z yOz),
(функция Q(х,г,z) интегрируеми върху променливи zИ х, тъй като части от повърхността се проектират върху равнината zOx).
Сумата от тези интеграли
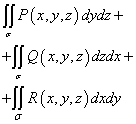
Наречен общ повърхностен интеграл от втори род и е обозначен
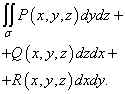
Изчисляване на повърхностен интеграл от втори род
Повърхностен интеграл от втори вид се изчислява чрез разлагане на общия повърхностен интеграл от втори вид на сумата от повърхностни интеграли (вижте края на предишния параграф) и редуциране на всеки от тях до двоен интеграл.
Нека разгледаме подробно изчисляването на интеграла
.
Нека повърхността σ дадено от уравнението z = z(х, г) . Означаваме положителната страна на повърхността, отрицателната страна и проекцията върху равнината xOy - дxy.
Така получаваме формула за изчисляване на повърхностния интеграл от втори вид:
Ако е избрана отрицателната страна на повърхността, тогава знакът на интеграла се променя:
Другите два отделни интеграла - членове на общия - се изчисляват по подобен начин:
Пример 2.
,
Където σ - горната страна на част от равнината, отрязана от равнини г= 0 и г= 4 и се намира в първия октант.
Решение. Чертежът е на снимката по-горе. По дефиниция получаваме сумата от три двойни интеграла:
Вторият интеграл е равен на нула, тъй като равнината σ успоредна на оста Ой. Следователно намираме първия и третия интеграл:
Остава само да се съберат всички отделни интеграли и да се получи общият повърхностен интеграл от втори вид:
.
Ако трябва да изчислите повърхностен интеграл от втори вид върху затворена повърхност, можете да отидете на троен интеграл, използвайки формулата на Остроградски. Тогава, ако функциите П(x,y,z) , Q(x,y,z) И Р(x,y,z) и техните частни производни , , са непрекъснати функции в областта У, която е ограничена от затворена повърхност σ , тогава при интегриране върху външната страна на повърхността равенството
Пример 3.Изчислете повърхностен интеграл от втори род
,
Където σ - външната страна на повърхността на конус, образувана от повърхност и равнина z = 2 .
Решение. Тази повърхност е повърхността на конус с радиус Р= 2 и височина ч= 2. Това е затворена повърхност, така че можете да използвате формулата на Остроградски. защото П = 3х , Q = 4г , Р = −z, тогава частните производни , , .
Преминаваме към тройния интеграл, който решаваме:
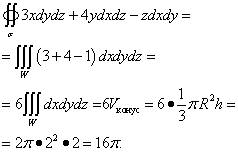
Още примери за изчисляване на повърхностни интеграли
Пример 4.Изчислете повърхностен интеграл от първи род
Където σ - странична повърхност на конуса при .
Решение. Тъй като частичните производни 
,
, Че
Редуцираме този повърхностен интеграл до двоен:
Проекция на повърхнина върху равнина xOyе окръжност с център в началото и радиус Р= 2, следователно, когато изчисляваме двойния интеграл, преминаваме към полярната координатна система. За да направите това, нека променим променливите:
Получаваме следния интеграл, който накрая решаваме:
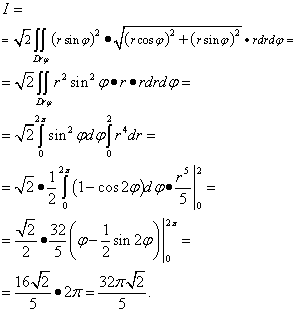
Пример 5.Изчислете повърхностен интеграл от втори род
,
Където σ - горната част на триъгълника, образуван от пресечната точка на равнината с координатните равнини.
Решение. Нека разделим този повърхностен интеграл на сумата от два интеграла
, Където
.
За изчисляване на интеграла аз1 σ до самолета yOz. Проекцията е триъгълник OCB, който е в самолета yOzограничаване на прави линии или, г= 0 и z= 0 . От уравнението на равнината се извежда. Следователно можем да изчислим интеграла аз1 :
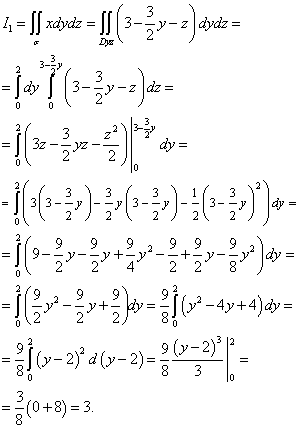
За изчисляване на интеграла аз2 , нека построим повърхностна проекция σ до самолета zOx. Проекцията е триъгълник AOC, което е ограничено от прави линии или , х= 0 и z= 0 . Изчисляваме:
Събираме двата получени интеграла и накрая получаваме този повърхностен интеграл:
.
Пример 6.Изчислете повърхностен интеграл от втори род
,
Където σ
- външната повърхност на пирамида, образувана от равнина 
и координатни равнини.
Пример 3.3.Изчислете работата на векторно поле
а = 2х 2 г аз – xy 2 й
от началото O до точка A(1;1), ако движението става по: а)линеен сегмент; б)дъги на парабола; V)прекъсната линия OBA, където B(1;0) (виж фиг. 3.1).
Решение . а)Уравнението на права линия OA има формата y=x. Позволявам x=t, тогава уравнението на правата линия в параметрична форма ще приеме формата:
x=t, y=t,
а при преминаване от А към В параметъра Tще се промени от 0 на 1. Тогава извършената работа ще бъде равна на
б)Позволявам x=t 2 , y=t, Тогава
x=t 2 , y=t, 0£ T£1 .
.
V)Уравнението на правата (OB) е г=0 (0£ х£1); уравнението на правата (BA) има формата х=1 (0 £ г£1). Тогава
, 
.
В резултат на това получаваме,
.
Коментирайте. Ако при двумерните полета уравнението на линията се описва от уравнението г=г(х), а променливата x варира от апреди b, тогава криволинейният интеграл на 2-ри ще бъде изчислен по формулата:
. (3.9)
Предишният пример може да бъде решен с помощта на тази формула без въвеждане на параметъра T.
Пример 3.4.Изчислете интеграл
,
където L е дъгата на параболата y=x 2 +1 от точка A(0;1) до точка B(2;5).
Решение . Нека направим чертеж (виж фиг. 3.2). От уравнението на параболата получаваме y"=2x. Тъй като върху дъгата на парабола ABпроменлива хсе променя от 0 на 2, тогава криволинейният интеграл, в съответствие с формула (3.9), ще приеме формата
4. ПОВЪРХНОСТНИ ИНТЕГРАЛИ
4.1. Повърхностни интеграли от първи род
Повърхностният интеграл от 1-ви род е обобщение на двойния интеграл и се въвежда по подобен начин. Помислете за някаква повърхност С, гладка или късово гладка, и приемете, че функцията f( x,y,z) е дефиниран и ограничен върху тази повърхност. Нека разделим тази повърхност на нпроизволни части. Площта на всеки парцел е означена с D s i. На всяка секция избираме точка с координати ( x i,y i,z i) и изчислете стойността на функцията във всяка такава точка. След това създаваме интегралната сума:
.
Ако има ограничение на интегралните суми при н®¥ (в този случай макс. D s i®0), т.е. такава граница не зависи нито от метода на разделяне, нито от избора на средни точки, тогава такава граница се нарича повърхностен интеграл от първи род :
. (4.1)
Ако функцията f( x,y,z) е непрекъснат на повърхността С, тогава границата (4.1) съществува.
Ако интегралната функция f( x,y,z)º1, тогава повърхностният интеграл от 1-ви род е равен на повърхността С:
. (4.2)
Да приемем, че е въведена декартова координатна система и всяка права линия, успоредна на оста Оз,може да премине повърхността Ссамо в една точка. След това уравнението на повърхността Сможе да се запише във формата
z = z(x,y)
и е уникално проектиран върху равнината xOy. В резултат на това повърхностният интеграл от 1-ви вид може да бъде изразен чрез двойния интеграл
.
(4.3)
Пример 4.1.Изчислете интеграл
,
Където С– част от коничната повърхност z 2 =х 2 +г£2,0 z£1.
Решение. Ние имаме
След това търсеният интеграл се трансформира в двоен интеграл
Където S xy- кръг х 2 +г 2 £1. Ето защо
.
4.2. Повърхностни интеграли от втори род
Нека векторно поле е определено в някакъв регион
а = a x аз + a y й + a z к
и всякаква двустранна повърхност С. Нека разделим повърхността по някакъв начин на елементарни области D S i. На всеки сайт избираме произволна точка P ази съставете интегралната сума:
, (4.4)
Където н (P i) – нормален вектор към дадена повърхност в точка P i. Ако има ограничение за такава сума под Г S i®0, тогава тази граница се нарича повърхностен интеграл от 2-ри род (или поток векторно поле а през повърхността С) и се обозначава със символа
или ,
Където д с =н ds.
Тъй като единичният нормален вектор има насочващи косинуси като координати н =(cosa, cosb, cosg). Че
По този начин изчисляването на повърхностни интеграли от 2-ри вид може да се сведе до изчисляване на повърхностни интеграли от 1-ви вид. Какво обаче За разлика от повърхностните интеграли от 1-ви вид, интегралите от 2-ри род зависят от избора на страната на повърхността. Преходът към другата страна на повърхността променя посоката на нормалата към повърхността и съответно знака на интеграла.
Разгледайте интеграла
.
Нека уравнението на повърхността има формата z=j( x,y) и положителната страна на тази повърхност ще се счита за тази, чиято нормална форма е с оста O zостър ъгъл. Тогава
cosg ds = dxdy.
Следователно разглежданият интеграл може да бъде записан във формата
.
Замяна zот j( x,y), стигаме до двойния интеграл
,
Където S xy– повърхностна проекция Сдо самолета xOy.
