МА. Хоёр дахь төрлийн гадаргуугийн интегралууд
Онолын доод хэмжээЭнэ сэдэв нь "" сэдвээр эхэлсэн муруйн ба гадаргуугийн интегралуудын хэлэлцүүлгийг үргэлжлүүлж байна. Энэ сэдэвтэй урьдчилан танилцахыг зөвлөж байна. Сэдвийн нарийн төвөгтэй байдлаас шалтгаалан муруй ба гадаргуугийн интегралууд
хоёр дахь төрлийг тусад нь авч үздэг. Хоёрдахь төрлийн гадаргуугийн интегралуудыг энд авч үзэх болно - магадгүй хамгийн төвөгтэй интеграл үйл ажиллагаа.
олон хувьсагчийн функцүүдийн шинжилгээ. Төлөвлөгөө нь хоёр дахь төрлийн муруйн интегралыг авч үзэхтэй бүрэн төстэй байх болно. Физик хэрэглээнээс эхэлцгээе.
Тэгээд бид албан ёсны математик тал руугаа шилжих болно.1. Хоёр дахь төрлийн гадаргуугийн интегралын физик хэрэглээ
Хоёрдахь төрлийн гадаргуугийн интегралыг нэвтрүүлэх хамгийн байгалийн арга бол зарим гадаргуугаар дамжин өнгөрөх шингэний урсгалыг авч үзэх явдал юм. Энгийн тохиолдлоор эхэлцгээе:
шингэн нь х тэнхлэгийн дагуу тогтмол хурдтайгаар урсдаг. Урсгалд перпендикуляр талбайг сонгож, дамжин өнгөрөх шингэний массыг олъё
түүнийг цагтаа. Энэ хугацаанд өндөр ба суурийн талбай бүхий "параллелепипед". Энэхүү "параллелепипедийн" масс
тэнцүү, шингэний нягт хаана байна.
Одоо шингэнийг x тэнхлэгт өнцгөөр хавтгайд параллель, гэхдээ хурдтай урсгана. Өмнөх сайтаас
тохиолдолд бид үүнийг абсцисса тэнхлэгт перпендикуляр байрлуулах болно. Цаг хугацаа өнгөрөхөд налуу "параллелепипед" дамжин өнгөрдөг (1-р зургийг үз). Түүний масс
тэнцүү . Нэгж хэвийн векторыг сайтад оруулах нь бидэнд бичих боломжийг олгодог гэдгийг анхаарна уу.
Модуль нь -тэй тэнцүү, чиглэл нь векторын чиглэлтэй давхцаж байгаа энгийн талбайн албан ёсны векторыг танилцуулав.
сайтын хувьд хэвийн. Дараа нь. Энэ тэмдэглэгээ нь шингэний хурдны векторын чиглэлийн талаар санаа зовохгүй байх боломжийг танд олгоно
сайт руу.Шингэн урсах талбайн жижиг байдал, тогтмол модуль ба хурдны чиглэлийн таамаглалаас татгалзах хэвээр байна. Дараа нь
гадаргуу нь жижиг хэсгүүдэд хуваагддаг бөгөөд тэдгээрийн дотор хурдны векторыг тогтмол гэж үзэж болно. Гадаргуугаар дамжин өнгөрөх шингэний масс нь
ойролцоогоор нийлбэрээр өгөгдсөн.
Гадаргууг хязгааргүй жижиг хэсгүүдэд хуваах хязгаарт тодорхой томъёог олж авна. Хязгаар нь хоёр дахь төрлийн гадаргуугийн интеграл юм..
Энэ хэсгийг бичихдээ ерөнхий физикийн тэнхимийн багшийн семинарын хичээлд ашигласан сургалтын материалын хэсгийг ашигласан болно.2. Хоёр дахь төрлийн гадаргуугийн интегралын тодорхойлолт
Одоо интегралын албан ёсны барилгын тухай. Вектор талбар нь гадаргуу дээр нэгдмэл байдаг тул аль талд нь байгааг тодруулах нь зүйтэй юм
гадаргуугийн хувьд интегралыг тооцоолно (шингэний урсгалыг тооцоолохтой адил: шингэн гадаргуу руу урсдаг эсвэл түүнээс урсдаг). Тиймээс үүнийг онцгойлон зааж өгсөн болно
Интеграци хийх гадаргуу нь хоёр талт эсвэл чиглүүлэх боломжтой байх ёстой (өөрөөр хэлбэл Мобиусын зурвас бүхэлдээ ажиллахгүй). Гадаргуу
нэн даруй чиглэсэн, өөрөөр хэлбэл. Гадаргуугийн нормын тодорхой чиглэлийг сонгосон (жишээлбэл, интегралыг бөмбөрцөг дээр тооцоолсон бол хэвийн байж болно.
бөмбөрцөгөөс эсвэл бөмбөрцөг рүү чиглэсэн). Талбайн бүрэлдэхүүн хэсгүүд нь ерөнхий тохиолдолд цэгийн функцууд юм. Интеграцийн гадаргуу
жижиг хэсгүүдэд хуваагдаж, хэсэг бүрт цэг сонгож, нийлбэрийг нэгтгэнэ
,
Хавтгай дээрх элементийн проекцын талбай хаана байна, энэ элементийн хавтгай дээрх проекцын талбай нь хаана байна
Энэ элементийн хавтгай дээрх проекц. Бид гадаргууг хуваасан бүх элементүүдийн нийлбэрийг хийдэг.
хамгийн том хэсэгчилсэн бүсийн голчийг тэг рүү чиглүүлж, хязгаарт очно. Хязгаар нь хоёр дахь төрлийн гадаргуугийн интеграл юм
.
Энэ интегралыг 1-р алхамаас хэлбэр рүү хэрхэн бууруулахыг үзүүлье. Үүнийг хийхийн тулд та цэвэр геометрийн шинж чанартай жижиг ухралт хийх хэрэгтэй болно. Байг
координатын тэнхлэгүүдийг огтолж буй онгоц (2-р зургийг үз). Энэ онгоцны эхний октантад байрлах хэсэг нь талбайтай. Та талбайг олох хэрэгтэй
хавтгайн өгөгдсөн хэсгийн координатын хавтгай дээрх бүх гурван ортогональ проекцууд. Мэдэгдэж байгаагаар зургийн проекцын талбай нь тухайн талбайн бүтээгдэхүүнтэй тэнцүү байна
зураг нь өөрөө ба зургийн хавтгай ба түүнийг төсөөлж буй хавтгай хоорондын өнцгийн косинус (3-р зургийг үз). Тэдгээр. үүсгэх өнцгүүдийг олох хэрэгтэй
координатын хавтгайтай хавтгай. Хоёр хавтгайн хоорондох өнцөг нь тэдгээрийн нормуудын хоорондох өнцөгтэй тэнцүү байна. Онгоцны хэвийн нэгж нь бүрэлдэхүүн хэсгүүдтэй,
нь түүний чиглэлийн косинусууд юм. Тиймээс хавтгай ба хавтгай хоорондын өнцөг тэнцүү байна (2-р зургийг үз), тиймээс .
Хязгааргүй жижиг талбайд ижил хамаарал хүчинтэй байх болно: . Мөн үүнтэй адил.
Эдгээр харилцааг харгалзан үзэхэд интеграл хэлбэрийг авна
.
Дашрамд хэлэхэд энэ бичлэгийн хэлбэр нь илүү харагдахуйц байдаг тул бид түүнтэй ажиллах болно.Нормативын чиглэлийг өөрчлөх нь интеграл тэмдгийг өөрчлөхөд хүргэдэг.
3. Хоёр дахь төрлийн гадаргуугийн интегралын тооцоо
Интегралыг гадарга руу чиглэсэн нормын чиглэлийн косинусуудыг агуулсан хэлбэр болгон бууруулсны дараа асуудал үндсэндээ хэвийн нэгжийг бичих хүртэл буурна.
Эхний төрлийн гадаргуугийн интегралын цаашдын тооцоогоор. Эдгээр үйлдлүүдэд зарим онцлог шинж чанарууд байдаг тул тооцооллыг нарийвчлан авч үзье
энэ төрлийн интегралууд.Интеграцийн гадаргууг тодорхой тэгшитгэлээр өгсөн тохиолдлоос эхэлье, жишээлбэл,
. Дараа нь хэвийн векторыг дараах байдлаар бичнэ.
,
болон гадаргуугийн талбайн элемент.
Үүний үр дүнд гадаргуугийн интеграл дараах хэлбэрийг авна.
, (1)
интеграцийн гадаргуугийн проекцийг харуулсан хавтгайн муж хаана байна.Интеграцийн гадаргуу нь хавтгай дээр (мөн тэгшитгэлээр өгөгдсөн) эсвэл хавтгай дээр зөв проекцлогдсон байж болно.
(болон тэгшитгэлээр өгөгдсөн). Дараа нь интегралыг тооцоолох томъёог бага зэрэг тохируулна.
(2)
эсвэл
. (3)
Мэдээжийн хэрэг, ийм томъёог цээжлэхийг зөвлөдөггүй: ямар нэг зүйлийг төөрөлдүүлэхэд хялбар байдаг - тэдгээрийг тодорхой зүйлтэй уялдуулан сэргээх нь дээр.
хэвийн вектор ба жижиг гадаргуугийн элементийн талбайн томъёонд үндэслэн дахин тооцоолно.Гадаргууг бүх гурван координатын хавтгайд зөв тусгасан тохиолдолд онцолсон нэг тохиолдол байдаг, жишээлбэл. гадаргуугийн тэгшитгэлээс аливаа хувьсагч
хоёрдмол утгагүй илэрхийлж болно. Дараа нь тооцооллыг ихээхэн хялбаршуулсан болно. Томъёоны бүтцэд анхаарлаа хандуулаарай (1) - (3). Тэд тус бүрт гурван байдаг
нэр томъёо, тэдгээрийн нэг нь бусдаасаа илүү энгийн харагддаг. Гадаргууг хавтгайд тусгах үед энэ нэр томъёо нь бүрэлдэхүүн хэсгийг агуулна
талбайнууд; хавтгайд төлөвлөхдөө энэ нь бүрэлдэхүүн хэсгийг агуулсан нэр томъёо юм; онгоцонд төлөвлөхдөө энэ нэр томъёо юм
бүрэлдэхүүн хэсгийг агуулсан. Хэрэв гадаргуу нь ямар ч координатын хавтгайд зөв проекц байвал интегралыг хуваана
Гурван хэсэгт хувааж, хэсэг бүрийг хамгийн тохиромжтой байдлаар төлөвлө:
.Эцэст нь, гадаргууг параметрээр тодорхойлох тохиолдол
.
Эхний төрлийн гадаргуугийн интегралыг тооцоолохдоо гурван Якобианыг анхаарч үзэх хэрэгтэй.
.
Нормаль косинусын чиглэлийг тэдгээрээр илэрхийлнэ.
,
гадаргуугийн элемент
.
Тиймээс интегралын хувьд бид олж авна
,
интеграцийн гадаргуутай харгалзах параметрийн өөрчлөлтийн хүрээ хаана байна.4. Стоксын томъёо. Остроградский-Гаусын томъёо
Хоёрдахь төрлийн гадаргуугийн интеграл нь янз бүрийн хэрэглээ, түүний дотор физик хэрэглээг олох хоёр томьёотой холбоотой юм.
Стоксын томъёо:
,
Хаана,
гадаргуу нь контурын дээгүүр сунасан, контурын хөндлөн огтлолцол нь баруун талын шурагны дүрмийн дагуу гадаргуугийн нормыг сонгоход нийцдэг.
Интеграцийн гадаргуу нь "нүх" байгаа бол тодруулга хийх шаардлагатай.
Ногоон томъёо нь энэ томьёоны онцгой тохиолдол юм. Нэмж дурдахад Стоксын томъёоноос хоёр дахь муруйн интегралын бие даасан байдлын нөхцөлийг дагаж мөрддөг.
замын хэлбэрээс нэг төрлийн.Остроградский-Гаусын томъёо.
Вектор талбарын хувьдтомъёо биелэгдсэн байна
гадаргуу нь эзлэхүүнийг хязгаарладаг газар.Остроградский-Гаусын томъёо нь өөр өөр хэрэглээтэй. Тэдгээрийн хоёрыг харцгаая. Нэгдүгээрт, биеийн эзэлхүүнийг тооцоолох боломжтой гэдгийг батлахад хялбар байдаг
томъёоны дагууХоёрдугаарт, заримдаа задгай гадаргуу дээр хоёр дахь төрлийн гадаргуугийн интегралыг тооцоолох шаардлагатай байдаг бөгөөд үүнд төвөгтэй тооцоолол орно.
Дараа нь гадаргууг хааж, интегралыг гурав дахин нэг болгон хувиргаж, нэмсэн гадаргуу дээрх интегралыг хасна (доорх жишээг үзнэ үү).Анхаарна уу. Стокс ба Остроградский-Гаусын томьёо нь векторын талбарын буржгар ба зөрүүг ашиглан вектор шинжилгээнд илүү тохиромжтой бичигдсэн байдаг.
Хоёр дахь төрлийн гадаргуугийн интегралыг тооцоолох жишээ
Жишээ 1. Хавтгай интеграл.. Дараа нь бид эллипс параболоидын хэсгүүдийг (гадаад хэвийн) авна.
Интегралыг хэлбэрээр дахин бичье
.
Интеграцийн гадаргуу - эллипс параболоид нь зөвхөн хавтгай дээр зөв проекцлагдсан тул гадаргуугийн тэгшитгэлийг хэлбэрээр бичнэ.
.
Нэгж хэвийн векторыг ол:.
Хавтгай муж дээрх давхар интеграл гэсэн ойлголтыг гадаргуу дээрх интегралын тохиолдолд хялбархан ерөнхийлж болно. (S) нь гадаргуу (хаалттай эсвэл нээлттэй) ба энэ гадаргуу дээрх цэгийн тасралтгүй функц байг. (S) хэсэг болгон хуваа
мөн эдгээр хэсгүүдийн талбайнууд болон эдгээр хэсгүүдэд байрлах аливаа цэгүүдийг зөвшөөр. Бүтээгдэхүүний нийлбэрийг нэгтгэх
Энэ нийлбэрийн хязгаарыг хуваах тоо хязгааргүй ихэсч, хэсэг тус бүр нь хязгааргүй буурч байгааг гадаргуу дээрх функцийн интеграл гэж нэрлэдэг.
Z тэнхлэгтэй параллель шулуун шугамууд гадаргууг зөвхөн нэг цэгээр огтолж байна (Зураг 48) ба проекц (S) нь XOY хавтгайд байна гэж үзье. Энгийн гадаргуугийн талбай (S) ба түүний проекцын харгалзах талбайн хоорондох холболтыг (26) ашиглан бид гадаргуу дээрх интегралыг (S) хавтгай талбай дээрх интеграл болгон бууруулж болно.
энэ тохиолдолд энэ нь тэгээс ялгаатай бөгөөд тухайн мужийн N цэг дэх функцийн утга нь тухайн M цэгийн гадаргуу дээр заасан функцийн утгатай давхцаж, проекц нь -тэй давхцаж байна гэж үзнэ. Хэрэв гадаргуугийн тэгшитгэл (S) нь тодорхой хэлбэрээр (22) өгөгдсөн бөгөөд функцийг координатаар илэрхийлсэн бол үүн дээр интегралдах үед функцийг илэрхийлэлд орлуулахад хангалттай. (29)-ийн баруун талд байгаа хуваагчийг (24) томъёоны гуравны нэгээр тодорхойлно.
Гадаргуугийн интегралууд нь -д заасан давхар интегралын бүх шинж чанартай байх нь ойлгомжтой, ялангуяа дундаж утгын теорем тэдгээрт нийцдэг гэдгийг анхаарна уу.
Одоо олон интегралын онолын нэг гол томьёо болох эзэлхүүн дээрх гурвалсан интеграл ба энэ эзлэхүүнийг хязгаарлаж буй гадаргуу дээрх интеграл (S) хоорондын холболтыг тогтоодог Остроградскийн томъёог баталъя. Z тэнхлэгтэй параллель шулуун шугамууд (S) хэрхэн, хаана огтлолцохыг бид хоёроос илүүгүй хугацаанд авч үзэх болно
оноо. Зураг дээрхтэй ижил тэмдэглэгээг хадгалцгаая. 40. Нормаль (S)-ийн чиглэлийг мөн авч үзье, энэ нь эзлэхүүний (V) (гадаад хэвийн) гадна чиглэсэн байна гэж үзье (Зураг 50). Энэ чиглэл нь гадаргуугийн дээд хэсэгт (I) OZ тэнхлэгтэй хурц өнцөг үүсгэдэг ба доод хэсэгт (I) мохоо өнцөг үүсгэдэг. Тиймээс, доод хэсэгт бид гадаргуугийн (5) цилиндртэй (50-р зураг) контактын шугам дээр байгааг тэмдэглэж байна. Формула (26) өгдөг
Деривативын хамт (S) хүртэлх мужид тасралтгүй байг. Функцийн гурвалсан интегралыг авч үзье.(16) томъёог ашигласнаар бид байна
Гэхдээ деривативын интеграл нь дээд ба доод хязгаар дахь деривативын эсрэг функцийн утгуудын зөрүүтэй тэнцүү байна.
Томъёоны дагуу (30) орлуулснаар бид интегралыг (S) дээр интеграл болгон бууруулж, гадаргуугийн (S) хэсгийн (I) хувьсах ординатыг агуулсан эхний интегралд бид эхний томъёог ашиглах шаардлагатай болно. (30) ба бид (II ) дээрх интегралыг олж авна, агуулсан хоёр дахь интегралд та (30) хоёр дахь томьёог ашиглах шаардлагатай бөгөөд (I) дээрх интегралыг авна.
Гадаргуугийн аль хэсэгт интеграл хийгдэж байгааг зааж өгсөн тул z-ийн тэмдэглэгээг бичих боломжгүй болсон. Баруун талд (II) ба (I) хэсгүүдийн интегралын нийлбэр, өөрөөр хэлбэл бүхэл бүтэн интеграл байна.
гадаргуу (S):
Хэрэв функцууд нь R функцийн шинж чанартай бол үүнийг харгалзан үзнэ
(31) дээр үндэслэн бид интеграцийн томъёог хэсгүүдээр бичиж болно.
Яг үүнтэй адил өөр хоёр функцийг авч үзвэл бид баталж чадна
Гурван томьёог нэр томъёогоор нэмснээр бид Остроградскийн томъёонд хүрнэ
(31,)-ийн нэгэн адил x ба y-тэй холбоотой деривативын хэсгүүдийн интегралчлалын томъёог бичнэ.
Товчхон байх үүднээс бид P, Q функцүүдийн x, y, z аргументуудыг энд бичээгүй боловч эдгээр нь эзлэхүүнээр тодорхойлогдсон функцууд бөгөөд тэдгээрийн деривативууд үргэлжилдэг гэдгийг санах хэрэгтэй.
Дараагийн бүлэгт бид Остроградскийн томъёог ашиглах олон тооны жишээг өгөх болно.
Хэмжигдэхүүнүүд нь гадаргуу (S) дээр тодорхойлогдсон функцууд юм. Бид тэдгээрийг тасралтгүй гэж үзсэн. Илүү ерөнхий таамаглал дэвшүүлж болно, тухайлбал, (S) нь хязгаарлагдмал тооны хэсгүүдэд хуваагдаж, тус бүр дээр заасан функцүүд тасралтгүй байна. Жишээлбэл, хэрэв (S) нь олон өнцөгт байвал ийм байх болно.
Томъёо (31) гаргахдаа бид тэнхлэгтэй параллель шулуун шугамууд тухайн бүсийн гадаргууг (S) хоёроос илүүгүй цэгээр огтолж байна гэж үзсэн. Энэ томьёог илүү ерөнхий хэлбэрийн хэсгүүдэд нэгтгэх нь тийм ч хэцүү биш юм. Хэрэв гадаргуу (S) нь дээд (II) ба доод хэсэг (I) -ээс гадна тэнхлэгтэй параллель гентрикс бүхий цилиндр хэлбэртэй хажуу талтай бол энэ тал дээр нэмж оруулаарай. (31) томъёоны баруун талд байгаа энэ хэсэг нь гадаргуугийн интегралын утгыг өөрчлөхгүй тул томьёоны нотолгоо бүхэлдээ хүчинтэй хэвээр байна. Илүү ерөнхий тохиолдолд өмнөх нөхцлүүдийг хангасан хязгаарлагдмал тооны хэсгүүдэд хуваахын тулд тэнхлэгт параллель генератор бүхий цилиндр гадаргууг ашиглахад хангалттай бөгөөд хэсэг бүрт (31) томъёог хэрэглэнэ. Энэ аргаар олж авсан томъёог нэмбэл бид зүүн талд бүх эзлэхүүний гурвалсан интегралтай болно. Баруун талд бид хуваасан хэсгүүдийн бүх гадаргуу дээрх интегралуудын нийлбэр байх болно (v). Дээр дурдсанчлан багасгасан туслах цилиндр гадаргуу дээрх интеграл нь тэгтэй тэнцүү байна. Тиймээс баруун талд нэмсэний үр дүнд бид анхны эзэлхүүний гадаргуу дээр (S) интегралтай болно. Тиймээс (31) томъёо нь илүү ерөнхий хэлбэрийн домайнуудад хүчинтэй болж хувирав.
Гадаргуугийн интеграл гэж нэрлэгддэг гадаргуу дээр тодорхойлогдсон функцүүдийн интегралуудыг авч үзье.Гадаргуугийн интегралын онол нь муруй шугаман интегралын онолтой олон талаараа төстэй. Эхний ба гадаргуугийн интегралууд байдаг
хоёр дахь төрлийн.
4.1. Эхний төрлийн гадаргуугийн интегралууд. f(x, y, z) функцийг үзье.
хэсэгчилсэн гөлгөр гадаргуу дээр тодорхойлогдсон S, хэсэгчилсэн гөлгөр контураар хязгаарлагдсан (Зураг 4.1). Үүнийг задалж үзье
тус тус ∆ s 1, ∆ s 2 ..., ∆ s n. S i, i = 1, n хэсэг бүрийн дотор дурын M i (x i, y i, z i) цэгийг авч, бид функцийн утгыг тооцоолж, дараах нийлбэрийг гаргана.
σ n= ∑ f (x i, y i, z i) ∆ s i | |||||
i= 1 | f (x, y, z) функцийн хувьд by |
||||
үүнийг интеграл гэж нэрлэдэг | |||||
гадаргуу С. | |||||
Үүний эцсийн хязгаар I | хичээж байхдаа | ||||
бүх хэсэгчилсэн гадаргуугийн диаметрүүдийн хамгийн том λ нь S i | |||||
1, n |
|||||
Хэрэв энэ нь байгаа бөгөөд гадаргууг хэсэгчилсэн байдлаар хуваах арга эсвэл цэгийн сонголтоос хамаарахгүй бол үүнийг гэнэ. эхний төрлийн гадаргуугийн интеграл (гадаргуу дээрх талбай)функцээс
f (x, y, z) гадаргуугийн дагуу S ба тэмдгээр тэмдэглэнэ | ∫∫ f(x, y, z) ds. |
|
Тиймээс, тодорхойлолтоор | ||
= ∫∫ f(x, y, z) ds. | ||
I = lim ∑ f(xi , yi , zi ) ∆ si | ||
λ → 0i = 1 | ||
Эхний төрлийн гадаргуугийн интеграл нь давхар интегралын ерөнхий дүгнэлт тул давхар интеграл байх нөхцөл, түүний шинж чанарууд нь нэгдүгээр төрлийн гадаргуугийн интеграл руу амархан шилждэг.
Эхний төрлийн гадаргуугийн интегралын тооцоо давхар интегралыг тооцоолоход бууруулна: гадаргуугийн тэгшитгэл дээр үндэслэн S,
интеграл нь хоёр хувьсагч болж хувирах бөгөөд тэдгээрийн хүрээ нь эдгээр хувьсагчид харгалзах координатын хавтгайд S гадаргуугийн проекц байх болно.
z = z (x, y) ба z (x, y) тэгшитгэлээр тодорхойлогддог S гадаргууг түүний z ′ x, z ′ y хэсэгчилсэн деривативуудын хамт үргэлжилсэн z ′ x, z ′ y хаалттай S xy мужид үргэлжилдэг ба энэ нь проекц юм. S гадаргууг xOy координатын хавтгайд, тэгвэл
∫∫ f(x, y, z) ds= ∫∫ f(x, y, z(x, y)) 1 + (z′ x ) 2 + (z′ y ) dxdy. | ||
S xy | ||
Энэ томьёо нь эхний төрлийн гадаргуугийн интегралыг S гадаргуугийн xOy координатын хавтгай дээрх проекц дээр давхар интегралаар илэрхийлнэ.
S гадаргуу дээрх эхний төрлийн гадаргуугийн интегралуудыг түүний проекц дээрх давхар интегралаар ижил төстэй аргаар тооцдог.
xOz ба yOz координатын хавтгайнууд: | |||
∫∫ f (x ,y ,z )ds = ∫∫ f (x ,y (x ,z ),z ) | 1+ (y ′ x )2 + (y ′ z )dxdz , | ||
S xz | |||
∫∫ f (x, y,z)ds= ∫∫ f (x(y,z), y,z) | 1 + (x′ y )2 + (x′ z )dydz. | ||
S yz | |||
Эхний төрлийн гадаргуугийн интегралуудыг ашиглан гадаргуугийн талбай, түүнчлэн масс, статик момент, инерцийн момент, гадаргуугийн массын тархалтын нягт нь мэдэгдэж буй материалын гадаргуугийн массын төвийн координатыг тооцоолох боломжтой.
Жишээ 4.1. Тооцоол
∫∫ 1 + 4 x 2 + 4 y 2 ds , S нь парабо-ын нэг хэсэг юм.
эргэлтийн loid z = 1 − x 2 − y 2, z = 0 хавтгайгаар таслагдсан.
Шийдэл. Гадаргууг зохион бүтээцгээе
S - хавтгайд xOy .
S xy проекц нь x 2 + y 2 = 1 тойргоор хүрээлэгдсэн тойрог юм (Зураг 1).
4.2). Өгөгдсөн гадаргуугийн интегралыг (4.2) томъёогоор тооцоолж, z ′ x = − 2 x , z ′ y = − 2 y-ийг олно. Дараа нь давхар үүрэг гүйцэтгэнэ
интеграл | туйл руу | координат, | S xy бол тойрог, |
||||||||
1 +4 x 2 +4 y 2 ds =∫∫ | 1+ 4x 2 + 4y 2 | 1 + 4 x2 + 4 y2 dxdy= |
|||||||||
S xy | |||||||||||
= ∫∫ (1 +4 x 2 +4 y 2 ) dxdy = | |||||||||||
S xy | |||||||||||
= ∫ d ϕ ∫ (1 +4 ρ 2 ) ρ d ρ =∫ | + ρ 4) | d ϕ= | ∫d ϕ. |
||||||||
4.2. Хоёр талт гадаргуу. S гадаргууг гэж нэрлэдэг
хоёр талт, хэрэв S гадаргуу дээр хэвтэх ямар нэгэн битүү контурын дагуу өнгөрч, түүний хилийг огтолдоггүй бол эхлэх цэг рүү буцах үед гадаргуу руу чиглэсэн хэвийн чиглэлийг өөрчлөхгүй. Үгүй бол гадаргууг нэг талт гэж нэрлэдэг. Хоёр талт гадаргуугийн жишээ: хавтгай, бөмбөрцөг болон z = z (x, y) тэгшитгэлээр тодорхойлогдсон аливаа гадаргуу, энд z = z (x, y), z ′ x (x, y), z ′ y (x) , y) - зарим хэсэгт тасралтгүй G. Нэг талт гадаргуугийн жишээ бол Мобиусын зурвас юм.
4.3. Хоёр дахь төрлийн гадаргуугийн интеграл. С - тэгшитгэлээр өгөгдсөн гөлгөр гадаргуу z = z(x, y) ба f(x, y, z) функц
гадаргуугийн цэгүүдэд тодорхойлогддог S.
Гадаргуугийн талуудын аль нэгийг, өөрөөр хэлбэл гадаргуугийн цэгүүд дэх хэвийн байдлын хоёр боломжит чиглэлийн аль нэгийг сонгоё (ингэж бид гадаргууг чиглүүлсэн). Хэрэв нормууд нь хурц өнцөг үүсгэдэг
Оз тэнхлэг , дараа нь бид ярилцах болногадаргуугийн дээд тал (хэвийн эерэг чиглэлийн тухай ), хэрэв хэвийн бол - Oz тэнхлэгтэй мохоо өнцөг, дараа нь бид гадаргуугийн доод талын тухай ярьж байна (хэвийн сөрөг чиглэл).
S гадаргууг дур мэдэн n хэсэгт S 1, S 2 ..., S n хэсэгт хувааж, (S xy ) i-ээр дамжуулан гадаргуугийн i-р хэсгийн проекцийг тэмдэглэе.
xOy онгоц руу. S i , i = 1, n хэсэгчилсэн гадаргуу бүрийн дотроос дурын M i (x i , y i , z i ) цэгийг сонгоод функцийн утгыг тооцоол.
Үүнд бид нийлбэрийг хийх болно
σ n= ∑ f (x i, y i, z i) ∆ s i, i = 1
Энд ∆ s i - талбай(S xy) i, S гадаргуугийн дээд талыг сонгосон бол нэмэх тэмдгээр, доод талыг сонгосон бол хасах тэмдгээр авна.
гадаргуу С. Энэ нийлбэрийг σ n гэж нэрлэдэг интеграл нийлбэр f(x, y, z) функцийн хувьд.
Интеграл нийлбэрийн эцсийн I хязгаар нь бүх проекцийн диаметрүүдийн хамгийн том λ нь (S xy ) i, хэрэв байгаа бол тэг рүү чиглэдэг.
S гадаргууг хуваах аргаас эсвэл цэгийн сонголтоос хамаарахгүй
M i (x i, y i, z i), тэгвэл энэ хязгаарыг дуудна хоёр дахь төрлийн функцийн гадаргуугийн интеграл f(x, y, z) хувьсагчаар гадаргуугийн сонгосон талын дагуу x ба y ба ∫∫ f (x, y, z) dxdy гэж тэмдэглэнэ. Тиймээс дагуу
тодорхойлолт
х ба у хувьсагчид дахь S гадаргуу.
Үүний нэгэн адил та y ба z хувьсагчид, x ба z хувьсагчдад S гадаргуугийн сонгосон тал дээр хоёр дахь төрлийн гадаргуугийн интегралуудыг тодорхойлж болно:
∫∫ f(x, y, z) dydz, | ∫∫ f(x, y, z) dxdz. |
P (x, y, z), Q (x, y, z), R (x, y, z) функцуудыг интегралчлах функцууд гэж үзье.
y ба z, x ба z, x ба y хувьсагчид тус тусын S гадаргуу. Интегралуудын нийлбэр
∫∫ P(x, y, z) dydz, | ∫∫ Q(x, y, z) dxdz, | ∫∫ R(x, y, z) dxdy | |
хоёр дахь төрлийн ерөнхий интеграл гэж нэрлэгдэх ба тэмдэглэнэ | |||
∫∫ P(x, y, z) dydz+ Q(x, y, z) dxdz+ R(x, y, z) dxdy. | |||
Бид S гадаргууг хоёр талт гэж үздэг ба интеграл нь түүний тодорхой тал хүртэл үргэлжилдэг тул Интеграцийн гадаргуугийн тал өөрчлөгдөхөд хоёр дахь төрлийн гадаргуугийн интеграл тэмдэг нь эсрэгээр өөрчлөгддөг- энэ бол эхний төрлийн гадаргуугийн интегралаас ялгаатай юм.
Хоёр дахь төрлийн гадаргуугийн интегралын тооцоо давхар интегралыг тооцоолоход бууруулна.
Баримтлагдсан (дээд талыг сонгох) гөлгөр S гадаргууг z = z (x, y) тэгшитгэлээр өгье, энд z (x, y) нь үргэлжилдэг.
хаалттай талбай S xy - S гадаргуугийн xOy хавтгайд проекц; f(x, y, z) функц нь S дээр тасралтгүй байна. Дараа нь томъёо хүчинтэй байна
∫∫ f(x, y, z) dxdy= ∫∫ f(x, y, z(x, y)) dxdy, | ||||
S xy | ||||
хоёр дахь төрлийн гадаргуугийн интегралыг x ба хувьсагчид дээр илэрхийлэх | ||||
давхар дамжуулан. Хэрэв бид S гадаргуугийн доод талыг сонговол урд талд нь |
||||
интеграл бол баруун талд хасах тэмдэг гарч ирнэ. | ||||
Томъёо нь мөн адил хүчинтэй | ||||
∫∫ f(x, y, z) dydz= ∫∫ f(x(y, z), y, z) dydz, | ||||
S yz | ||||
∫∫ f(x, y, z) dxdz= ∫∫ f(x, y(x, z), z) dxdz, | ||||
S xz | ||||
хаана гадаргуу С | тэгшитгэлийн дагуу | x = x(y, z) | ||
y = y(x, z) ба Syz | болон S xz - | S гадаргуугийн проекцууд тус тус | ||
yOz ба xOz онгоцууд.
Ерөнхий хэлбэрийн интеграл (4.6)-ийг тооцоолохын тулд S гадаргуу нь бүх гадаргуу дээр өвөрмөц проекцтой бол (4.7)-(4.9) томъёог ашиглана.
координатын хавтгайнууд. Илүү төвөгтэй тохиолдолд S гадаргууг заасан шинж чанартай хэсгүүдэд хуваадаг бөгөөд ерөнхий интегралыг эдгээр хэсгүүдийн дээр интеграл хэлбэрээр үзүүлэв.
Жишээ 4.2.Тооцоо
∫∫ (y 2 + z 2 ) dxdy , S нь дээд тал юм
гадаргуу z = | 1 − x 2 | Таслагдсан хавтгай |
||||||||
шоо y = 0, y = 1. | ||||||||||
Шийдэл. Тэгшитгэл x 2 + z 2 = 1 - |
||||||||||
generatrix бүхий дугуй цилиндрийг тодорхойлсон, |
||||||||||
Oy тэнхлэгтэй параллель байх ба хавтгай нь y = 0 ба |
||||||||||
y = 1 | Зэрэгцээ | зохицуулах |
||||||||
xOz хавтгай (Зураг. | Төсөл |
|||||||||
xOy хавтгай дээрх S гадаргуу нь |
||||||||||
тэгш өнцөгт S xy тэгш бус байдлаар тодорхойлогддог − 1 ≤ x ≤ 1, | 0 ≤ y ≤ 1. |
|||||||||
Дараа нь (4.7) томъёогоор бид байна | ||||||||||
∫∫ (y2 + z2 ) dxdy= ∫∫ (y2 + (1 − x2 )) dxdy= ∫ dx∫ (y2 − x2 + 1) dy= |
||||||||||
S xy | −1 | |||||||||
+ (1− x 2 )y ) | ||||||||||
= ∫ dx ( | ||||||||||
−1 | ||||||||||
− x2 ) dx | ||||||||||||||||||||||||||||||
= ∫ ( | ||||||||||||||||||||||||||||||
−1 | −1 | |||||||||||||||||||||||||||||
Жишээ 4.3. Тооцоол | ||||||||||||||||||||||||||||||
∫∫ xdydz+ ydxdz+ zdxdy, S нь дээд | ||||||||||||||||||||||||||||||
хавтгайн хэсгийн тал x + z − 1 = 0 | ||||||||||||||||||||||||||||||
y = 0, y = 4 ба хавтгайгаар таслагдана | ||||||||||||||||||||||||||||||
эхний октантад байрладаг (Зураг 4.4). | ||||||||||||||||||||||||||||||
Шийдэл. S гадаргуугийн проекц | ||||||||||||||||||||||||||||||
xOy хавтгай нь S xy тэгш өнцөгт, | ||||||||||||||||||||||||||||||
0 ≤ x ≤ 1 тэгш бус байдлаар тодорхойлогддог, | ||||||||||||||||||||||||||||||
0 ≤ y ≤ 4 . S гадаргуугийн проекц | ||||||||||||||||||||||||||||||
yOz хавтгай нь тэгш өнцөгт юм | Тэгш бус байдлаар тодорхойлогддог S yz |
|||||||||||||||||||||||||||||
0 ≤ z ≤ 1,0 ≤ y ≤ 4. S хавтгай нь хавтгайд перпендикуляр байдаг тул |
||||||||||||||||||||||||||||||
xOz , тэгвэл∫∫ ydxdz = 0. Дараа нь (4.7) ба (4.9) томъёогоор бид байна. |
||||||||||||||||||||||||||||||
∫∫ xdydz+ ydxdz+ zdxdy= ∫∫ (1 − z) dydz+ |
||||||||||||||||||||||||||||||
S yz | ||||||||||||||||||||||||||||||
+ ∫∫ (1 − x) dxdy= ∫ dy∫ (1 − z) dz+ ∫ dy∫ (1 − x) dx= |
||||||||||||||||||||||||||||||
S xy | ||||||||||||||||||||||||||||||
− z ) | (1− x) | |||||||||||||||||||||||||||||
2 ∫ | dy = 4. |
|||||||||||||||||||||||||||||
= ∫ dy − | + ∫ dy − | |||||||||||||||||||||||||||||
4.4. Остроградскийн томъёо. Остроградскийн томьёо нь битүү гадаргуу дээрх гадаргуугийн интеграл ба энэ гадаргуугаар хязгаарлагдах орон зайн муж дээрх гурвалсан интегралын хоорондох холболтыг тогтоодог..
V нь S гадаргуугаар хязгаарлагдсан ердийн битүү муж байх ба P(x, y, z), Q(x, y, z), R(x, y, z) функцууд байг.
тухайн бүс нутагт эхний эрэмбийн хэсэгчилсэн деривативын хамт тасралтгүй байна. Дараа нь дараах томъёог баримтална.
∫∫∫( | ∂P | ∂Q | ∂ R ) dxdydz= ∫∫ Pdydz+ Qdxdz+ Rdxdy, (4.10) |
|||
∂x | ∂y | ∂z | ||||
дуудсанОстроградскийн томъёо 1 .
Остроградскийн томъёог ашиглан битүү гадаргуу дээрх гадаргуугийн интегралыг тооцоолоход тохиромжтой.
Жишээ 4.4.Остроградскийн томъёог ашиглан тооцоол
∫∫ xdydz + ydxdz + zdxdy , | Хаана С | ||||||||||||||||||||||||||
пирамидын тал | хязгаарлагдмал | онгоцууд | |||||||||||||||||||||||||
x + y + z = 1, | x= 0,y= 0, | z= 0 (Зураг 4.5). | |||||||||||||||||||||||||
дагуу | |||||||||||||||||||||||||||
Остроградский: | |||||||||||||||||||||||||||
П(x,y,z)= x,Q(x,y,z)= y,Р(x,y,z)= z. | |||||||||||||||||||||||||||
Дараа нь: ∂ П+ | ∂ Q+ | ∂Р | = 1+ 1+ 1= 3,мөн бид олдог | ||||||||||||||||||||||||
∂x | ∂y | ∂z | |||||||||||||||||||||||||
1− x | 1 −x−y | ||||||||||||||||||||||||||
∫∫ xdydz + ydxdz + zdxdy = 3 ∫∫∫ dxdydz = 3 ∫ dx ∫ dy | ∫ dz = | ||||||||||||||||||||||||||
1− x | 1 −x−y | 1− x | |||||||||||||||||||||||||
= 3 ∫ dx ∫ dy ∫ dz = 3 ∫ dx ∫ (1 − x − y ) dy = | |||||||||||||||||||||||||||
y 2 | 1− x | ||||||||||||||||||||||||||
3 ∫ dx ( y − xy − | |||||||||||||||||||||||||||
−2 x+1 | 3 (x− 1) | ||||||||||||||||||||||||||
= 3 ∫ (1 −x−x+x2 − | ) dx = | ∫ ( x − 1) 2 dx = | |||||||||||||||||||||||||
Тайлбар 4.1.Эхний болон хоёр дахь төрлийн гадаргуугийн интегралуудын хоорондын холболт нь муруй шугаман интегралуудын хоорондын холболттой төстэй.
∫∫ е ( x , y , z ) dxdy = ∫∫ е ( x , y , z ) cosα ds ,
∫∫ е ( x , y , z ) dydz = ∫∫ е ( x , y , z ) cosβ ds ,
∫∫ е ( x , y , z ) dxdz = ∫∫ е ( x , y , z ) cosγ ds ,
Хаана cosα ,cosβ ,cosγ - харгалзах нормын чиглэлийн косинусууд
гадаргуугийн сонгосон тал. ,y) | талбайд тасралтгүй Сxy- гадаргуугийн төсөөлөл С |
||||||||||||||||||||||
онгоц руу xOy;Л | - контур, | хязгаарлах | гадаргуу | С ; л – |
|||||||||||||||||||
сансрын шугамын проекц Лонгоц руу | xOy , | байх |
|||||||||||||||||||||
талбайг хязгаарласан үржүүлгийн газар Д. Дээд талыг нь сонгоцгооё |
|||||||||||||||||||||||
гадаргуу С. Хэрэв функцууд П(x, y, z), Q(x, y, z), Р(x, y, z) | Үргэлжилсэн |
||||||||||||||||||||||
түүний нэгдүгээр эрэмбийн хэсэгчилсэн деривативын хамт |
|||||||||||||||||||||||
гадаргуу С, дараа нь дараах томъёог агуулна. | |||||||||||||||||||||||
∫ Pdx + Qdy + Рдз = | |||||||||||||||||||||||
= ∫∫ | (∂ Q | ∂ П) dxdy + ( | ∂Р | ∂ Q) dydz + (∂ П | ∂ Р) dxdz | ||||||||||||||||||
∂x | ∂y | ∂y | ∂z | ∂z | ∂x | ||||||||||||||||||
(Л- эерэг чиглэлд хөдөлдөг) | дуудсан томъёо |
||||||||||||||||||||||
Хэрэв гадаргуу шиг бол Сталбайг авна Дгадаргуу дээр xOy |
|||||||||||||||||||||||
(z= 0 ), дараа нь (4.11) -ээс бид Гринийн томъёог олж авна | ∂Q | ∂ П) dxdy . | |||||||||||||||||||||
∫ П ( x , y ) dx + Q ( x , y ) dy = ∫∫ ( | |||||||||||||||||||||||
∂x | ∂y | ||||||||||||||||||||||
Тиймээс Грийн томъёо нь Стоксын томъёоны онцгой тохиолдол юм. |
|||||||||||||||||||||||
Томъёоны хоёр дахь төрлийн гадаргуугийн интеграл гэдгийг анхаарна уу |
|||||||||||||||||||||||
Стокс (4.11) эхнийх нь гадаргуугийн интегралаар сольж болно |
|||||||||||||||||||||||
төрөл. Дараа нь энэ томъёо хэлбэрийг авна | |||||||||||||||||||||||
∫ Pdx + Qdy + Рдз = | |||||||||||||||||||||||
∂Q | ∂П | ∂Р | ∂Q | ∂П | ∂Р | ||||||||||||||||||
= ∫∫ | ) cos α + ( | ) cos β + ( | ) cos γ | ||||||||||||||||||||
∂x | ∂y | ∂y | ∂z | ∂z | ∂x | ds , | |||||||||||||||||
Хаана cos α , cos β , cos γ , | гэсэн үг | хөтөч | косинусууд | ||||||||||||||||||||
гадаргуугийн сонгосон талтай харгалзах. | |||||||||||||||||||||||
томъёог ашиглан | тооцоолох |
||||||||||||||||||||||
∫ x 2 y 3 dx + dy + zdz , | тойрог, | тэгшитгэлээр өгөгдсөн |
|||||||||||||||||||||
x 2 + y 2 + 1, z = 0 . | Гадаргуу Сбөмбөрцгийн дээд тал нь үйлчилдэг |
||||||||||||||||||||||
x 2+ y 2+ z 2= 1, | z> 0 (Лэерэг чиглэлд явдаг). |
||||||||||||||||||||||
Интеграл нь муруйн сегмент дээр биш, харин хязгаарлагдмал гадаргуу дээр явагддаг тохиолдолд. Муруй шугаман интегралуудын нэгэн адил гадаргуугийн интегралууд нь эхний төрөл ба хоёр дахь төрөл юм.
Эхний төрлийн гадаргуугийн интеграл хэлбэрээр бичсэн
Хаана е(М) = е(x,y,z) нь гурван хувьсагчийн функц ба гадаргуу σ - энэ функцийг нэгтгэх талбар. Хэрэв е(x,y,z) нэгдэлтэй тэнцүү бол гадаргуугийн интеграл нь гадаргуугийн талбайтай тэнцүү байна.
Маш жижиг үртэй нэлээд том наранцэцгийг төсөөлөөд үз дээ. Дараа нь наранцэцгийн гадаргуу дээр байрлах маш жижиг үрийн гадаргуугийн нийлбэрээс наранцэцгийн гадаргууг тооцоолж болно - энэ нь гадаргуугийн интегралын хялбаршуулсан тайлбар байж болно. Яагаад тэр вэ?
Гадаргуугийн интегралын илүү албан ёсны тодорхойлолт руу шилжье. Гадаргуу σ гэж хуваагддаг nΔ талбайтай хэсгүүд σ 1 , Δ σ 2 , ..., Δ σ n. Хэрэв та хэсэгчилсэн гадаргуу бүр дээр дурын цэгийг сонговол (үр) Мбикоординаттай ( ζ би, η би, ς би,), тэгвэл бид дүгнэж болно
Энэ нийлбэрийг функцийн интеграл нийлбэр гэж нэрлэдэг е(М) гадарга дээр σ . Одоо бид ийм жижиг хэсгүүдийн тоог дээд зэргээр нэмэгдүүлэх болно, хамгийн том диаметр нь Δ σ би- эсрэгээр нь багасгах. Хэрэв хэсгүүдийн голчуудын хамгийн том интеграл нийлбэр нь тэг байх хандлагатай бол (өөрөөр хэлбэл бид аль хэдийн тэмдэглэсэнчлэн бүх хэсгүүд нь маш бага байдаг) хязгаартай бол энэ хязгаарыг гэнэ. Эхний төрлийн гадаргуугийн интеграл функцээс е(М) гадарга дээр σ .
Эхний төрлийн гадаргуугийн интегралын тооцоо
Гадаргууг нь тавь σ тэгшитгэлээр өгөгдсөн z = z(x, y) , түүний хавтгай дээрх проекц xOyталбай юм Дxy, функц байх үед z = z(x, y) ба түүний хэсэгчилсэн деривативууд нь бүс нутагт тасралтгүй байна Дxy.
Жишээ 1.
Хаана σ - эхний октант дахь онгоцны хэсэг.
Шийдэл. Зурах:
Хавтгайн тэгшитгэлээс бид "zet" илэрхийллийг олж авна. 
.
Дараа нь хэсэгчилсэн деривативууд нь: , ба
.
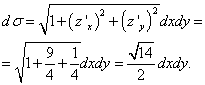Гадаргуу σ нь зурагт үзүүлсэн гурвалжин юм ABC, ба түүний хавтгай дээрх проекц xOy- гурвалжин AOB, энэ нь шулуун шугамаар хязгаарлагддаг x = 0 , y= 0 ба 3 x + y= 6. Гадаргуугийн интегралаас давхар интеграл руу шилжиж, үүнийг шийдье.
.
Хоёр дахь төрлийн гадаргуугийн интегралын тухай ойлголт
Хоёрдахь төрлийн гадаргуугийн интегралын тодорхойлолт руу шилжихээсээ өмнө гадаргуугийн талууд ба чиглэсэн гадаргуугийн тухай ойлголттой танилцах шаардлагатай.
Орон зайд гөлгөр гадаргууг өгье σ . Энэ гадаргуу дээрх дурын цэгийг сонгоцгооё Мба түүгээр дамжуулан гадаргуу дээр хэвийн векторыг зурна. Цэгээр дамжуулан Мбид мөн гадаргуу дээр хийх болно σ гадаргуугийн хилтэй нийтлэг цэггүй дурын контур σ . Бүрэн зогсоох Мхэвийн векторын хамт бид контурын дагуу хөдөлж, хэвийн вектор гадаргууд байнга перпендикуляр байх болно. σ . Цэг буцаж ирэхэд МЭхний байрлалд хоёр тохиолдол байж болно: хэвийн векторын чиглэл ижил хэвээр байх эсвэл эсрэгээр өөрчлөгдөх болно.
Хэрэв хэвийн векторын чиглэл өөрчлөгдөхгүй бол гадаргуу σ хоёр талт гэж нэрлэдэг. Хэрэв контурыг давах үед хэвийн векторын чиглэл эсрэгээр өөрчлөгдвөл гадаргууг нэг талт гэж нэрлэдэг. Хоёр талт гадаргууг чиглүүлсэн гадаргуу, нэг талт гадаргууг чиглээгүй гадаргуу гэж нэрлэдэг.
Нэг талт гадаргуугийн жишээ бол Мобиусын тууз (дээрх зурган дээр) бөгөөд үүнийг нэг талдаа 180 градус эргүүлж, дараа нь үзүүрийг нь наасан туузаар хийж болно. Энд хамгийн чухал зүйл бол: нэг талт гадаргуугийн хувьд хоёр дахь төрлийн гадаргуугийн интеграл гэсэн ойлголтыг оруулаагүй болно .
Тиймээс бид зөвхөн хоёр талт гадаргууг авч үзэх болно. Хоёр талт гадаргуугийн жишээ бол хавтгай, бөмбөрцөг, эллипсоид, параболоид юм.
Хоёр талт гадаргуугийн эерэг тал нь хэвийн векторын чиглэлийг тодорхойлдог. Гадаргуугийн эсрэг талыг сөрөг гэж нэрлэдэг. Гадаргуугийн эерэг тал нь түүний дээд тал юм. Хэрэв нэгж хэвийн векторууд тэнхлэгтэй хурц өнцөг үүсгэдэг бол Оз, дараа нь гадаргуугийн дээд талыг сонгоно z = z(x, y) , хэрэв өнцөг нь мохоо бол гадаргуугийн доод тал.
Эхний төрлийн гадаргуугийн интегралын нэгэн адил гадаргууг хувааж болно nхэсгүүд. Эхний төрлийн гадаргуугийн интегралын тухай ойлголтыг боловсруулахдаа интеграл нийлбэр нь функцийн утгыг үржүүлсэн хэсэг бүрийн талбайг багтаасан болно. е(Мби). Хоёрдахь төрлийн гадаргуугийн интегралын хувьд хэсгүүдийн талбайг бус, харин координатын хавтгай дээрх проекцын талбайг авна. . Гурван хувьсагчийн функцийг эхний төрлийн интегралаас ялгахын тулд бид үүнийг тэмдэглэв. Р(x,y,z) . Дараа нь интеграл нийлбэрийг дараах байдлаар бичнэ.
,
хаана Δ сби- гадаргуугийн хажуугийн хэсгүүдийн координатын тэнхлэгт дурдсан проекцуудын талбайнууд (одоогоор бид тэнхлэг дээр гэж үзэх болно. xOy).
Ийм конвенц, тэмдэглэгээгээр хоёр дахь төрлийн гадаргуугийн интегралын тодорхойлолт нь эхний төрлийн интегралын тодорхойлолттой төстэй юм. Тухайлбал: Хоёрдахь төрлийн гадаргуугийн интеграл нь тухайн гадаргуугийн хэсгүүдийн хамгийн том диаметр нь тэг байх хандлагатай байдаг тул өгөгдсөн интеграл нийлбэрийн хязгаар юм.
Үүнийг ингэж бичсэн байна.
.
Энэ тохиолдолд функц Р(x,y,z) хувьсагч дээр интегралдах боломжтой xТэгээд y, учир нь гадаргуугийн хэсгүүдийг хавтгай дээр буулгасан xOy.
Үүний нэгэн адил бид хоёр дахь төрлийн бусад хоёр гадаргуугийн интегралыг бичиж болно.
(функц П(x,y,z) хувьсагч дээр интегралдах боломжтой yТэгээд z yOz),
(функц Q(x,y,z) хувьсагч дээр интегралдах боломжтой zТэгээд x, учир нь гадаргуугийн хэсгүүд нь хавтгайд тусгагдсан байдаг zOx).
Эдгээр интегралуудын нийлбэр
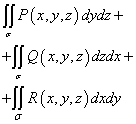
дуудсан Хоёр дахь төрлийн гадаргуугийн ерөнхий интеграл болон томилогдсон
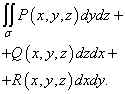
Хоёр дахь төрлийн гадаргуугийн интегралын тооцоо
Хоёр дахь төрлийн гадаргуугийн интегралыг гадаргуугийн ерөнхий интегралыг гадаргуугийн интегралын нийлбэр болгон задалж (өмнөх догол мөрийн төгсгөлийг харна уу) тус бүрийг давхар интеграл болгон бууруулж тооцно.
Интегралын тооцоог нарийвчлан авч үзье
.
Гадаргууг нь тавь σ тэгшитгэлээр өгөгдсөн z = z(x, y) . Бид гадаргуугийн эерэг тал, сөрөг тал, хавтгай дээрх проекцийг тэмдэглэдэг xOy - Дxy.
Тиймээс бид хоёр дахь төрлийн гадаргуугийн интегралыг тооцоолох томъёог олж авна.
Хэрэв гадаргуугийн сөрөг талыг сонгосон бол интегралын тэмдэг өөрчлөгдөнө.
Үлдсэн хоёр тусдаа интеграл - ерөнхий нэгийн нөхцлүүд - ижил төстэй байдлаар тооцогдоно.
Жишээ 2.
,
Хаана σ - онгоцоор таслагдсан онгоцны нэг хэсгийн дээд тал y= 0 ба y= 4 ба эхний октантад байрлана.
Шийдэл. Зургийг дээрх зурагт үзүүлэв. Тодорхойлолтоор бид гурван давхар интегралын нийлбэрийг олж авна.
Хоёр дахь интеграл нь тэгтэй тэнцүү, учир нь хавтгай σ тэнхлэгтэй зэрэгцээ Өө. Тиймээс бид эхний болон гурав дахь интегралуудыг олно.
Үлдсэн зүйл бол бүх бие даасан интегралуудыг нэгтгэж, хоёр дахь төрлийн ерөнхий гадаргуугийн интегралыг олж авах явдал юм.
.
Хэрэв та хаалттай гадаргуу дээр хоёр дахь төрлийн гадаргуугийн интегралыг тооцоолох шаардлагатай бол та очиж болно гурвалсан интеграл, Остроградскийн томъёог ашиглан. Дараа нь, хэрэв функцууд П(x,y,z) , Q(x,y,z) Мөн Р(x,y,z) ба тэдгээрийн хэсэгчилсэн дериватив , , нь домайн дахь тасралтгүй функцууд юм В, энэ нь битүү гадаргуугаар хязгаарлагддаг σ , дараа нь гадаргуугийн гадна талд нэгтгэх үед тэгш байдал
Жишээ 3.Хоёр дахь төрлийн гадаргуугийн интегралыг тооцоол
,
Хаана σ - гадаргуу ба хавтгайгаас үүссэн конусын гадаргуугийн гадна тал z = 2 .
Шийдэл. Энэ гадаргуу нь радиустай конусын гадаргуу юм Р= 2 ба өндөр h= 2 . Энэ бол хаалттай гадаргуу тул та Остроградскийн томъёог ашиглаж болно. Учир нь П = 3x , Q = 4y , Р = −z, дараа нь хэсэгчилсэн деривативууд , , .
Бид гурвалсан интеграл руу шилжиж, үүнийг шийднэ.
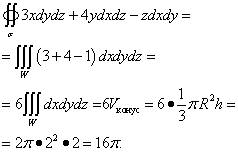
Гадаргуугийн интегралыг тооцоолох бусад жишээ
Жишээ 4.Эхний төрлийн гадаргуугийн интегралыг тооцоол
Хаана σ - конусын хажуугийн гадаргуу нь .
Шийдэл. Хэсэгчилсэн деривативуудаас хойш 
,
, Тэр
Бид энэ гадаргуугийн интегралыг хоёр дахин багасгаж:
Хавтгай дээрх гадаргуугийн проекц xOyнь эх болон радиус дээр төвтэй тойрог юм Р= 2, тиймээс давхар интегралыг тооцоолохдоо бид туйлын координатын систем рүү шилждэг. Үүнийг хийхийн тулд хувьсагчдыг өөрчилье:
Бид дараах интегралыг олж, эцэст нь шийддэг.
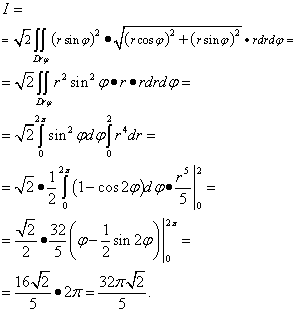
Жишээ 5.Хоёр дахь төрлийн гадаргуугийн интегралыг тооцоол
,
Хаана σ - координатын хавтгайтай хавтгай огтлолцсоноор үүссэн гурвалжны дээд хэсэг.
Шийдэл. Энэ гадаргуугийн интегралыг хоёр интегралын нийлбэрт хуваая
, Хаана
.
Интегралыг тооцоолохын тулд I1 σ онгоц руу yOz. Төсөл нь гурвалжин юм OCB, онгоцонд байгаа yOzшулуун шугамыг хязгаарлах эсвэл, y= 0 ба z= 0. Хавтгайн тэгшитгэлээс гарна. Тиймээс бид интегралыг тооцоолж болно I1 :
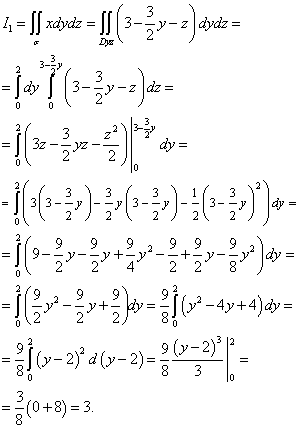
Интегралыг тооцоолохын тулд I2 , гадаргуугийн проекцийг байгуулъя σ онгоц руу zOx. Төсөл нь гурвалжин юм AOCшулуун шугамаар хүрээлэгдсэн , эсвэл , x= 0 ба z= 0. Бид тооцоолно:
Бид үүссэн хоёр интегралыг нэмж, эцэст нь энэ гадаргуугийн интегралыг олж авна.
.
Жишээ 6.Хоёр дахь төрлийн гадаргуугийн интегралыг тооцоол
,
Хаана σ
- хавтгайгаар үүссэн пирамидын гаднах гадаргуу 
ба координат хавтгай.
Жишээ 3.3.Вектор талбайн ажлыг тооцоол
а = 2x 2 y би – xy 2 j
О эхлэлээс A(1;1) цэг хүртэл, хэрэв хөдөлгөөн нь дагуу явбал: A)шугамын сегмент; б)параболын нумууд; V)эвдэрсэн шугам OBA, энд B(1;0) (3.1-р зургийг үз).
Шийдэл . A) OA шулуун шугамын тэгшитгэл нь хэлбэртэй байна y=x. Болъё x=t, дараа нь параметрийн хэлбэрийн шулуун шугамын тэгшитгэл нь дараах хэлбэртэй болно.
x=t, y=t,
мөн А-аас В руу шилжих үед параметр т 0-ээс 1 болж өөрчлөгдөнө.Тэгвэл хийсэн ажил нь тэнцүү болно
б)Болъё x=t 2 , y=t, Дараа нь
x=t 2 , y=t, 0£ т£1 .
.
V)Шугамын тэгшитгэл (OB) байна y=0 (0£ x£1); шугамын тэгшитгэл (BA) хэлбэртэй байна x=1 (0 £ y£1). Дараа нь
, 
.
Үүний үр дүнд бид,
.
Сэтгэгдэл. Хэрэв хоёр хэмжээст талбайн хувьд шугамын тэгшитгэлийг тэгшитгэлээр тодорхойлно y=y(x), хувьсагч x нь өөр өөр байна аөмнө б, дараа нь 2-р муруйн интегралыг дараах томъёогоор тооцоолно.
. (3.9)
Өмнөх жишээг энэ томъёог ашиглан параметрийг оруулахгүйгээр шийдэж болно т.
Жишээ 3.4.Интегралыг тооцоолох
,
Энд L нь параболын нум юм y=x A(0;1) цэгээс B(2;5) цэг хүртэл 2 +1.
Шийдэл . Зураг зурцгаая (3.2-р зургийг үз). Параболын тэгшитгэлээс бид олж авна y"=2x. Параболагийн нуман дээр байгаа тул ABхувьсагч x 0-ээс 2 хүртэл өөрчлөгдвөл (3.9) томъёоны дагуу муруйн интеграл хэлбэрийг авна.
4. Гадаргуугийн интегралууд
4.1. Эхний төрлийн гадаргуугийн интегралууд
1-р төрлийн гадаргуугийн интеграл нь давхар интегралын ерөнхий дүгнэлт бөгөөд үүнтэй төстэй байдлаар танилцуулагддаг. Зарим гадаргууг авч үзье С, гөлгөр эсвэл хэсэгчлэн гөлгөр ба f( функцийг гүйцэтгэнэ гэж үзье. x,y,z) энэ гадаргуу дээр тодорхойлогдсон бөгөөд хязгаарлагдмал. Энэ гадаргууг хувацгаая nдурын хэсгүүд. Талбай бүрийн талбайг D гэж тэмдэглэсэн с би. Хэсэг бүр дээр бид координат бүхий цэгийг сонгоно ( x i ,y i ,z i) ба ийм цэг тус бүрийн функцийн утгыг тооцоол. Үүний дараа бид интеграл нийлбэрийг үүсгэнэ.
.
Хэрэв интеграл нийлбэрийн хязгаар байгаа бол n®¥ (энэ тохиолдолд хамгийн их D с би®0), өөрөөр хэлбэл. Ийм хязгаар нь хуваах арга эсвэл дундын цэгийн сонголтоос хамаарахгүй тул ийм хязгаар гэж нэрлэдэг. Эхний төрлийн гадаргуугийн интеграл :
. (4.1)
Хэрэв функц f( x,y,z) гадаргуу дээр тасралтгүй байна С, тэгвэл (4.1) хязгаар байна.
Хэрэв интеграл функц f( x,y,z)º1, тэгвэл 1-р төрлийн гадаргуугийн интеграл нь гадаргуугийн талбайтай тэнцүү байна С:
. (4.2)
Декартын координатын систем, тэнхлэгтэй параллель дурын шулуун шугамыг нэвтрүүлсэн гэж үзье Оз,гадаргууг гаталж болно Сзөвхөн нэг цэг дээр. Дараа нь гадаргуугийн тэгшитгэл Схэлбэрээр бичиж болно
z = z(x,y)
бөгөөд энэ нь онгоцонд өвөрмөц байдлаар тусгагдсан байдаг xOy. Үүний үр дүнд 1-р төрлийн гадаргуугийн интегралыг давхар интегралаар илэрхийлж болно.
.
(4.3)
Жишээ 4.1.Интегралыг тооцоолох
,
Хаана С- конус хэлбэрийн гадаргуугийн хэсэг z 2 =x 2 +y£2.0 z£1.
Шийдэл. Бидэнд байгаа
Дараа нь шаардлагатай интегралыг давхар интеграл болгон хувиргана
Хаана S xy- тойрог x 2 +y 2 £1. Тийм ч учраас
.
4.2. Хоёр дахь төрлийн гадаргуугийн интегралууд
Зарим мужид вектор талбарыг зааж өгье
а = а х би + а y j + a z к
болон аливаа хоёр талт гадаргуу С. Гадаргууг ямар нэгэн байдлаар энгийн хэсгүүдэд хуваацгаая D S i. Сайт бүр дээр бид дурын P цэгийг сонгоно биболон интеграл нийлбэрийг зохио:
, (4.4)
Хаана n (П и) – цэг дээрх өгөгдсөн гадаргуу руу чиглэсэн хэвийн вектор П и. Хэрэв Д-д ийм хэмжээний хязгаар байгаа бол S i®0 байвал энэ хязгаарыг дуудна 2-р төрлийн гадаргуугийн интеграл (эсвэл урсгал вектор талбар а гадаргуугаар дамжин С) ба тэмдгээр тэмдэглэнэ
эсвэл ,
Хаана г с =n ds.
Нэгж хэвийн вектор нь координатаараа чиглэлтэй косинустай байдаг n =(cosa, cosb, cosg). Тэр
Тиймээс 2-р төрлийн гадаргуугийн интегралын тооцоог 1-р төрлийн гадаргуугийн интегралын тооцоолол болгон бууруулж болно. Гэсэн хэдий ч юу 1-р төрлийн гадаргуугийн интегралаас ялгаатай нь 2-р төрлийн интеграл нь гадаргуугийн хажуугийн сонголтоос хамаардаг. Гадаргуугийн нөгөө тал руу шилжих нь гадаргуугийн хэвийн чиглэлийг өөрчилдөг бөгөөд үүний дагуу интегралын тэмдэг өөрчлөгддөг..
Интегралыг авч үзье
.
Гадаргуугийн тэгшитгэлийг хэлбэртэй болго z=j( x,y) ба энэ гадаргуугийн эерэг талыг О тэнхлэгтэй хэвийн хэлбэрүүд гэж үзнэ zхурц булан. Дараа нь
cosg ds = dxdy.
Тиймээс авч үзэж буй интегралыг хэлбэрээр бичиж болно
.
Солих z j( x,y), бид давхар интегралд хүрнэ
,
Хаана S xy- гадаргуугийн проекц Сонгоц руу xOy.
