MA. Integrali di superficie di seconda specie
Minimo teoricoQuesto argomento continua la discussione sugli integrali curvilinei e di superficie iniziata nell'argomento "". Si consiglia di familiarizzare con questo argomento in anticipo. A causa della maggiore complessità dell'argomento, integrali curvilinei e di superficie
le seconde tipologie vengono considerate separatamente. Qui vengono discussi gli integrali di superficie del secondo tipo, forse l'operazione integrale più complessa
analisi di funzioni di più variabili. La pianta sarà del tutto simile alla considerazione di un integrale curvilineo del secondo genere. Cominciamo con le applicazioni fisiche,
e poi passeremo all'aspetto matematico formale.1. Applicazioni fisiche dell'integrale di superficie del secondo tipo
Il modo più naturale per introdurre un integrale di superficie del secondo tipo è considerare il flusso di un fluido attraverso una superficie. Cominciamo con un caso semplice:
il liquido scorre lungo l'asse x a velocità costante. Selezioniamo un'area perpendicolare al flusso e troviamo la massa di fluido che la attraversa
lei in tempo. Durante questo periodo, un "parallelepipedo" con altezza e superficie di base di . La massa di questo “parallelepipedo”
uguale a, dove è la densità del liquido.
Ora lascia che il liquido scorra parallelo al piano ad angolo rispetto all'asse x, ma sempre con una velocità. Il sito del precedente
In questo caso lo posizioneremo comunque perpendicolare all'asse delle ascisse. Nel tempo, un “parallelepipedo” inclinato lo attraversa (vedi Fig. 1). La sua massa
uguale a . Si noti che l'introduzione di un vettore normale unitario nel sito ci consente di scrivere .
Si introduce un vettore formale di un'area elementare, il cui modulo è uguale a , e la sua direzione coincide con la direzione del vettore
normale al sito. Poi. Questa notazione permette di non preoccuparsi della direzione del vettore velocità del fluido rispetto a
al sito.Resta da abbandonare la piccolezza dell'area attraverso la quale scorre il liquido e l'assunzione di un modulo e di una direzione di velocità costanti. Poi
la superficie è divisa in piccole parti, all'interno delle quali il vettore velocità può essere considerato costante. La massa di liquido che passa attraverso la superficie è
è approssimativamente dato dalla somma.
La formula esatta si otterrà nel limite di dividere la superficie in parti infinitesimali. Il limite è un integrale di superficie del secondo tipo:.
Durante la stesura di questa sezione è stato utilizzato un frammento di materiale didattico di un insegnante del Dipartimento di Fisica Generale, da lui utilizzato nei corsi di seminario.2. Definizione di integrale di superficie del secondo tipo
Passiamo ora alla costruzione formale dell'integrale. Dato che il campo vettoriale è integrato sulla superficie, è opportuno chiarire da che parte
superficie, viene calcolato l'integrale (come quando si calcola il flusso di un liquido: il liquido scorre nella superficie o ne esce). Pertanto, è particolarmente specificato
che la superficie su cui viene effettuata l'integrazione deve essere bilaterale o orientabile (vale a dire che il nastro di Möbius nel suo insieme non funzionerà). Superficie
immediatamente orientato, cioè viene selezionata una certa direzione della normale alla superficie (ad esempio, se l'integrale viene calcolato su una sfera, la normale può essere
diretto dalla sfera o nella sfera). Le componenti del campo sono, nel caso generale, funzioni di un punto. Superficie di integrazione
viene diviso in piccole parti, in ciascuna parte viene selezionato un punto e viene compilata la somma
,
dove è l'area della proiezione dell'elemento sul piano, è l'area della proiezione di questo elemento sul piano, è l'area
proiezione di questo elemento su un piano. Effettuiamo la sommatoria su tutti gli elementi in cui è suddivisa la superficie:
e andare al limite, portando a zero il diametro della regione parziale più grande. Il limite è un integrale di superficie del secondo tipo
.
Mostriamo come ridurre questo integrale alla forma del passaggio 1. Per fare ciò dovrai fare una piccola digressione di carattere prettamente geometrico. Lascia che ci sia
piano che interseca gli assi delle coordinate (vedi Fig. 2). La parte di questo piano situata nel primo ottante ha un'area di . Devi trovare la zona
tutte e tre le proiezioni ortogonali di una data parte del piano su piani coordinati. Come è noto, l'area di proiezione di una figura è pari al prodotto dell'area
la figura stessa e il coseno dell'angolo compreso tra il piano della figura e il piano su cui è proiettata (vedi Fig. 3). Quelli. è necessario trovare gli angoli che formano
piano con piani coordinati. L'angolo tra due piani è uguale all'angolo tra le loro normali. L'unità normale al piano ha componenti,
quali sono i suoi coseni di direzione. Pertanto, l'angolo tra il piano e il piano è uguale (vedi Fig. 2), e quindi .
La stessa relazione varrà per aree infinitesime: . E allo stesso modo.
Tenendo conto di queste relazioni, l'integrale assume la forma
.
A proposito, questa forma di registrazione è più visiva, quindi lavoreremo con essa.Invertendo la direzione della normale l’integrale cambia segno.
3. Calcolo dell'integrale di superficie di seconda specie
Dopo aver ridotto l'integrale ad una forma contenente i coseni di direzione della normale alla superficie, il problema si riduce essenzialmente a scrivere la normale unitaria
con ulteriore calcolo dell'integrale di superficie del primo tipo. Ci sono alcune specificità in queste azioni, quindi esaminiamo il calcolo in dettaglio
integrali di questo tipo.Cominciamo con il caso in cui la superficie di integrazione è data da un'equazione esplicita, ad esempio,
. Quindi il vettore normale viene scritto come segue:
,
e l'elemento di superficie.
Di conseguenza, l’integrale di superficie assume la seguente forma:
, (1)
dove è la regione del piano in cui è proiettata la superficie di integrazione.Può darsi che la superficie di integrazione sia correttamente proiettata sul piano (e data dall'equazione) o sul piano
(ed è dato dall'equazione). Quindi la formula con cui viene calcolato l'integrale viene leggermente modificata:
(2)
O
. (3)
Naturalmente, non è consigliabile memorizzare tali formule: è facile confondere qualcosa, è meglio ripristinarle in relazione a uno specifico
calcolo nuovamente, basato sulla formula del vettore normale e dell'area di un piccolo elemento di superficie.C'è un caso evidenziato in cui la superficie è proiettata correttamente su tutti e tre i piani delle coordinate, ad es. dall'equazione di superficie qualsiasi variabile
può essere espresso senza ambiguità. Quindi il calcolo è notevolmente semplificato. Prestare attenzione alla struttura delle formule (1) - (3). In ognuno di essi ce ne sono tre
termini, e uno di essi sembra più semplice degli altri. Quando si proietta una superficie su un piano, questo termine contiene il componente
campi ; quando proiettato su un piano è il termine contenente il componente ; quando proiettato su un piano, questo è il termine
componente contenente. Se la superficie si proietta correttamente su qualsiasi piano di coordinate, dividiamo l'integrale
in tre parti e progetta ciascuna parte nel modo più conveniente:
.Infine il caso di definizione parametrica della superficie
.
Come quando si calcola un integrale di superficie del primo tipo, è necessario considerare tre Jacobiani:
.
I coseni direzionali della normale si esprimono attraverso essi:
,
elemento di superficie
.
Quindi, per l'integrale otteniamo
,
dove è l'intervallo di modifiche dei parametri corrispondente alla superficie di integrazione.4. Formula di Stokes. Formula di Ostrogradskij-Gauss
L'integrale di superficie del secondo tipo è associato a due formule che trovano diverse applicazioni, anche in campo fisico.
Formula di Stokes:
,
Dove ,
la superficie è allungata sul contorno, la traslazione del contorno è coerente con la scelta della normale alla superficie secondo la regola della vite destrorsa.
Sono necessari chiarimenti qualora la superficie di integrazione presenti “buchi”.
La formula di Green è un caso speciale di questa formula. Inoltre dalla formula di Stokes segue la condizione per l'indipendenza dell'integrale curvilineo della seconda
un po' dalla forma del sentiero.Formula di Ostrogradskij-Gauss.
Per un campo vettorialela formula è soddisfatta
dove la superficie limita il volume.La formula di Ostrogradsky-Gauss ha diverse applicazioni. Diamo un'occhiata a due di loro. Innanzitutto è facile dimostrare che il volume di un corpo può essere calcolato
secondo la formulaIn secondo luogo, a volte è necessario calcolare un integrale di superficie del secondo tipo su una superficie aperta, il che comporta calcoli macchinosi.
Quindi la superficie viene chiusa, l'integrale viene convertito in triplo e l'integrale sulla superficie aggiunta viene sottratto (vedere l'esempio sotto).Nota. Le formule di Stokes e Ostrogradsky-Gauss sono scritte più convenientemente nell'analisi vettoriale utilizzando l'arricciatura e la divergenza del campo vettoriale.
Esempi di calcolo degli integrali di superficie del secondo tipo
Esempio 1. Integrale piano.. Quindi otteniamo) parti di un paraboloide ellittico (normale esterno).
Riscriviamo l'integrale nella forma
.
La superficie di integrazione - un paraboloide ellittico - è proiettata correttamente solo sul piano, quindi scriviamo l'equazione della superficie nella forma
.
Trovare il vettore normale dell'unità:.
Il concetto di integrale doppio su una regione piana può essere facilmente generalizzato al caso dell'integrazione su una superficie. Sia (S) una superficie (chiusa o aperta) e una funzione continua di un punto su tale superficie. Rompi (S) in parti
e lasciare che le aree di queste parti e tutti i punti situati su queste parti. Compilare la somma dei prodotti
Il limite di questa somma con un aumento infinito del numero di divisioni e una diminuzione infinita di ciascuna delle parti è chiamato integrale della funzione sulla superficie
Supponiamo che rette parallele all'asse Z intersechino la superficie in un solo punto (Fig. 48) e sia la proiezione (S) sul piano XOY. Utilizzando la formula (26), che stabilisce la connessione tra l'area della superficie elementare (S) e la corrispondente area della sua proiezione, possiamo ridurre l'integrale sulla superficie (S) all'integrale sull'area piana:
in questo caso si assume che sia diverso da zero e che il valore della funzione nel punto N della regione coincida con il valore della funzione specificata sulla superficie in quel punto M, la cui proiezione coincide con . Se l'equazione della superficie (S) è data in forma esplicita (22) e la funzione è espressa in termini di coordinate, allora quando si integra su di essa è sufficiente sostituire la funzione nell'espressione. Il denominatore sul lato destro di (29) è determinato dalla terza delle formule (24).
Si noti che gli integrali di superficie hanno ovviamente tutte le proprietà di un integrale doppio indicate in , in particolare per essi vale il teorema del valor medio.
Dimostriamo ora una delle formule principali nella teoria degli integrali multipli: la formula di Ostrogradsky, che stabilisce una connessione tra l'integrale triplo su un volume e l'integrale sulla superficie (S) che delimita questo volume. Considereremo come e dove le linee rette parallele all'asse Z si intersecano (S) in non più di due
punti. Manteniamo la stessa notazione della Fig. 40. Introduciamo anche la direzione della normale a (S), e supponiamo che sia diretta all'esterno del volume (V) (normale esterna) (Fig. 50). Questa direzione forma un angolo acuto con l'asse OZ nella parte superiore della superficie (I), e un angolo ottuso nella parte inferiore (I). Pertanto, nella parte inferiore, notiamo che sulla linea di contatto della superficie (5) con il cilindro sporgente (Fig. 50). La formula (26) dà
Sia, insieme alla derivata, continua nella regione fino a (S). Consideriamo l'integrale triplo della funzione e utilizzando la formula (16) avremo:
Ma l'integrale della derivata è uguale alla differenza tra i valori della funzione antiderivativa ai limiti superiore e inferiore:
Sostituendo con secondo le formule (30), riduciamo l'integrazione ad integrazione su (S), e nel primo integrale, contenente l'ordinata variabile della parte (I) della superficie (S), dovremo utilizzare la prima delle formule (30), e otteniamo l'integrale su (II ), nel secondo integrale contenente dovrai utilizzare la seconda delle formule (30), e otterrai l'integrale su (I):
I simboli per z non possono più essere scritti, poiché viene indicato su quale parte della superficie viene eseguita l'integrazione. Sul lato destro c'è la somma degli integrali sulle parti (II) e (I), cioè l'integrale sull'intero
superfici (S):
Se sono funzioni che hanno le proprietà della funzione R, allora, tenendo conto di ciò
Sulla base della (31), possiamo scrivere la formula di integrazione per parti:
Esattamente allo stesso modo, prendendo altre due funzioni potremmo dimostrare
Sommando termine per termine le tre formule ottenute si arriva alla formula di Ostrogradskij
Analogamente alla (31), vengono scritte le formule di integrazione per parti delle derivate rispetto a xey.
Per brevità non scriviamo qui gli argomenti x, y, z delle funzioni P, Q, ma dobbiamo ricordare che si tratta di funzioni definite in volume e continue con le loro derivate.
Nel prossimo capitolo forniremo un gran numero di esempi dell'applicazione della formula di Ostrogradsky.
Le quantità sono funzioni definite sulla superficie (S). Li abbiamo considerati continui. Si può fare un'assunzione più generale, cioè supporre che (S) sia diviso in un numero finito di pezzi, su ciascuno dei quali le funzioni indicate siano continue. Questo sarà il caso, ad esempio, se (S) è un poliedro.
Nel derivare la formula (31), abbiamo assunto che le linee rette parallele all'asse intersecano la superficie (S) della regione in non più di due punti. Non è difficile generalizzare questa formula ad aree di forma più generale. Notiamo innanzitutto che se la superficie (S), oltre alla parte superiore (II) e alla parte inferiore (I), presenta una parte laterale cilindrica con generatrici parallele all'asse, allora su questa parte laterale e sommando questa parte a destra della formula (31) non cambia il valore dell'integrale di superficie, quindi l'intera dimostrazione della formula rimane valida. In un caso più generale è sufficiente utilizzare superfici cilindriche con generatrici parallele all'asse da dividere in un numero finito di parti che soddisfino le condizioni precedenti, e applicare a ciascuna parte la formula (31). Sommando le formule così ottenute avremo sul lato sinistro un integrale triplo su tutto il volume. Sul lato destro avremo la somma degli integrali su tutte le superfici di quelle parti in cui abbiamo diviso (v). Gli integrali sulle superfici cilindriche ausiliarie ridotte, come sopra indicato, sono pari a zero. Pertanto, come risultato dell'addizione sul lato destro, avremo un integrale sulla superficie (S) del volume originale. La formula (31) risulta quindi valida per domini di forma più generale.
Consideriamo gli integrali di funzioni definite su superfici, i cosiddetti integrali di superficie. La teoria degli integrali di superficie è per molti versi simile alla teoria degli integrali curvilinei. Esistono integrali di superficie del primo e
del secondo tipo.
4.1. Integrali di superficie del primo tipo. Sia la funzione f(x, y, z)
definita su una superficie liscia a tratti S, delimitata da un contorno liscio a tratti (Fig. 4.1). Analizziamolo
rispettivamente ∆ s 1, ∆ s 2 ..., ∆ s n. Prendendo un punto arbitrario M i (xi, y i, z i) all'interno di ciascuna parte S i, i = 1, n, calcoliamo il valore della funzione in esso e facciamo la seguente somma:
σ n= ∑ f (x i, y i, z i) ∆ s io | |||||
io= 1 | per la funzione f (x, y, z) di |
||||
che si dice integrale | |||||
superficie S. | |||||
Il limite finale I di questo | mentre si sforza | ||||
il più grande λ dei diametri di tutte le superfici parziali S i | |||||
1, n |
|||||
se esiste e non dipende né dal metodo di divisione della superficie in parziali né dalla scelta dei punti, allora si chiama integrale di superficie del primo tipo (su superficie) dalla funzione
f (x, y, z) lungo la superficie S ed è indicato con il simbolo | ∫∫ f(x, y, z) ds. |
|
Quindi, per definizione | ||
= ∫∫ f(x, y, z) ds. | ||
io = lim ∑ f(xi , yi , zi ) ∆ si | ||
λ → 0i = 1 | ||
L'integrale di superficie del primo tipo è una generalizzazione dell'integrale doppio, pertanto le condizioni per l'esistenza dell'integrale doppio e le sue proprietà si trasferiscono facilmente all'integrale di superficie del primo tipo.
Calcolo degli integrali di superficie del primo tipo si riduce al calcolo degli integrali doppi: basandosi sull'equazione della superficie S,
l'integrando viene trasformato in due variabili, il cui intervallo sarà la proiezione della superficie S sul piano delle coordinate corrispondente a queste variabili.
Sia la superficie S definita dall'equazione z = z (x, y) e z (x, y) continua insieme alle sue derivate parziali z ′ x, z ′ y in un dominio chiuso S xy, che è la proiezione di la superficie S sul piano delle coordinate xOy, quindi
∫∫ f(x, y, z) ds= ∫∫ f(x, y, z(x, y)) 1 + (z′ x ) 2 + (z′ y ) dxdy. | ||
Sxy | ||
Questa formula esprime l'integrale di superficie del primo tipo tramite l'integrale doppio sulla proiezione della superficie S sul piano delle coordinate xOy.
Gli integrali di superficie del primo tipo sulla superficie S si calcolano in modo simile tramite integrali doppi sulle sue proiezioni su
coordinare i piani xOz e yOz rispettivamente: | |||
∫∫ f (x ,y ,z )ds = ∫∫ f (x ,y (x ,z ),z ) | 1+ (y′ x )2 + (y′ z )dxdz , | ||
S xz | |||
∫∫ f (x, y,z)ds= ∫∫ f (x(y,z), y,z) | 1 + (x′ y )2 + (x′ z )dydz. | ||
S yz | |||
Utilizzando gli integrali di superficie del primo tipo, è possibile calcolare l'area superficiale, nonché la massa, i momenti statici, i momenti di inerzia e le coordinate del centro di massa per superfici di materiali con una densità di distribuzione della massa superficiale nota.
Esempio 4.1. Calcolare
∫∫ 1 + 4 x 2 + 4 y 2 ds , dove S è parte del parabo-
loid della rivoluzione z = 1 − X 2 − y 2 , tagliato dal piano z = 0 .
Soluzione. Progettiamo la superficie
S al piano xOy .
La proiezione S xy è un cerchio delimitato dal cerchio x 2 + y 2 = 1 (Fig.
4.2). Calcoleremo l'integrale di superficie dato utilizzando la formula (4.2), per la quale troviamo z ′ x = − 2 x , z ′ y = − 2 y . Quindi, impegnandosi in doppio
integrante | al polare | coordinate, | Sxy è un cerchio, |
||||||||
1 +4 x 2 +4 y 2 ds =∫∫ | 1+ 4x 2 + 4 anni 2 | 1 + 4 x2 + 4 y2 dxdy= |
|||||||||
Sxy | |||||||||||
= ∫∫ (1 +4 x 2 +4 y 2 ) dxdy = | |||||||||||
Sxy | |||||||||||
= ∫ d ϕ ∫ (1 +4 ρ 2 ) ρ d ρ = ∫ | +ρ4) | dϕ= | ∫dϕ. |
||||||||
4.2. Superfici bifacciali. La superficie S si chiama
bilaterale, se si attraversa lungo qualsiasi contorno chiuso che giace sulla superficie S e non ne interseca i confini, quando si ritorna al punto di partenza, non cambia la direzione della normale alla superficie. Altrimenti la superficie è detta unilaterale. Esempi di superfici a due lati: piano, sfera e qualsiasi superficie definita dall'equazione z = z (x, y), dove z = z (x, y), z ′ x (x, y), z ′ y (x , y) - continuo in qualche areaG. Un esempio di superficie unilaterale è il nastro di Möbius.
4.3. Integrale di superficie del secondo tipo. Lasciamo che S - superficie liscia data dall'equazione z = z(x, y) e funzione f(x, y, z)
definita nei punti della superficie S.
Selezioniamo uno dei lati della superficie, cioè una delle due possibili direzioni della normale ai punti della superficie (questo è il modo in cui abbiamo orientato la superficie). Se le normali formano angoli acuti con
Asse Oz , poi ne parleremo il lato superiore della superficie (intorno alla direzione positiva della normale ), e se le normali sono – angoli ottusi con l'asse di Oz, allora stiamo parlando del lato inferiore della superficie (la direzione negativa della normale).
Dividiamo arbitrariamente la superficie S in n parti S 1, S 2 ..., S n, e con (S xy ) i indichiamo la proiezione della i-esima parte della superficie
al piano xOy. All'interno di ciascuna superficie parziale S i , i = 1, n, scegli un punto arbitrario M i (xi , y i , z i ) e calcola il valore della funzione
in esso faremo la somma
σ n= ∑ f (x i, y i, z i) ∆ s i, i = 1
dove ∆ s i - area(S xy) i, presa con segno più se è selezionato il lato superiore della superficie S e con segno meno se è selezionato il lato inferiore
superficie S. Questa sommaσ n si chiama somma integrale per la funzione f(x, y, z).
Il limite finale I della somma integrale, essendo il maggiore λ di tutti i diametri di proiezione (S xy ) i tende a zero, se esiste e
non dipende né dal metodo di partizionamento della superficie S né dalla scelta dei punti
M i (xi, y i, z i), allora questo limite si chiama integrale di superficie del secondo tipo di funzione f(x, y, z) lungo il lato selezionato della superficie in base alle variabili xey e indicati con ∫∫ f (x, y, z) dxdy. Quindi, secondo
definizione
superficie S nelle variabili x e y.
Allo stesso modo, è possibile definire integrali di superficie del secondo tipo su un lato selezionato della superficie S nelle variabili y e z, nelle variabili x e z:
∫∫ f(x, y, z) dydz, | ∫∫ f(x, y, z) dxdz. |
Siano P (x, y, z), Q (x, y, z), R (x, y, z) funzioni integrabili su
superficie S nelle variabili y e z, x e z, x e y, rispettivamente. Somma di integrali
∫∫ P(x, y, z) dydz, | ∫∫ Q(x, y, z) dxdz, | ∫∫ R(x, y, z) dxdy | |
si chiama integrale generale del secondo tipo e si denota con | |||
∫∫ P(x, y, z) dydz+ Q(x, y, z) dxdz+ R(x, y, z) dxdy. | |||
Poiché consideriamo la superficie S bilaterale e l'integrale si estende su un certo lato di essa, allora quando cambia il lato della superficie di integrazione, l'integrale di superficie del secondo tipo cambia di segno in senso opposto– questa è la sua differenza dall’integrale di superficie del primo tipo.
Calcolo degli integrali di superficie del secondo tipo si riduce al calcolo di integrali doppi.
Sia una superficie liscia orientata S (scegliere il lato superiore) data dall'equazione z = z (x, y), dove z (x, y) è continua in
area chiusa S xy - proiezione della superficie S sul piano xOy; la funzione f(x, y, z) è continua su S. Allora la formula è valida
∫∫ f(x, y, z) dxdy= ∫∫ f(x, y, z(x, y)) dxdy, | ||||
Sxy | ||||
esprimendo l'integrale di superficie del secondo tipo sulle variabili x e | ||||
attraverso il doppio. Se scegliamo il lato inferiore della superficie S, quindi di fronte |
||||
integrale, apparirà un segno meno sul lato destro. | ||||
Le formule sono altrettanto valide | ||||
∫∫ f(x, y, z) dydz= ∫∫ f(x(y, z), y, z) dydz, | ||||
S yz | ||||
∫∫ f(x, y, z) dxdz= ∫∫ f(x, y(x, z), z) dxdz, | ||||
S xz | ||||
dove la superficie S | secondo le equazioni | x = x(y, z) | ||
y = y(x, z) e Syz | e Sxz- | rispettivamente proiezioni della superficie S | ||
piani yOz e xOz.
Per calcolare l'integrale di forma generale (4.6), si utilizzano le formule (4.7)–(4.9) se la superficie S è proiettata univocamente su tutti
piani coordinati. Nei casi più complessi, la superficie S è divisa in parti che hanno le proprietà indicate e l'integrale generale è presentato sotto forma di integrali su queste parti.
Esempio 4.2.Calcola
∫∫ (y 2 + z 2 ) dxdy , dove S è il lato superiore
superficie z = | 1-x2 | Taglio piatto |
||||||||
dadi y = 0, y = 1. | ||||||||||
Soluzione. L'equazione x 2 + z 2 = 1 - |
||||||||||
viene specificato un cilindro circolare con una generatrice, |
||||||||||
parallelo all'asse Oy e il piano y = 0 e |
||||||||||
y = 1 | parallelo | coordinata |
||||||||
piano xOz (fig. | Proiezione |
|||||||||
la superficie S sul piano xOy è |
||||||||||
rettangolo S xy definito dalle disuguaglianze − 1 ≤ x ≤ 1, | 0 ≤ y ≤ 1. |
|||||||||
Quindi, per la formula (4.7) abbiamo | ||||||||||
∫∫ (y2 + z2 ) dxdy= ∫∫ (y2 + (1 − x2 )) dxdy= ∫ dx∫ (y2 − x2 + 1) dy= |
||||||||||
Sxy | −1 | |||||||||
+ (1− x 2 )y ) | ||||||||||
= ∫ dx ( | ||||||||||
−1 | ||||||||||
− x2) dx | ||||||||||||||||||||||||||||||
= ∫ ( | ||||||||||||||||||||||||||||||
−1 | −1 | |||||||||||||||||||||||||||||
Esempio 4.3. Calcolare | ||||||||||||||||||||||||||||||
∫∫ xdydz+ ydxdz+ zdxdy, dove S è il superiore | ||||||||||||||||||||||||||||||
lato della parte del piano x + z − 1 = 0 | ||||||||||||||||||||||||||||||
tagliato dagli aerei y = 0, y = 4 e | ||||||||||||||||||||||||||||||
situato nel primo ottante (Fig. 4.4). | ||||||||||||||||||||||||||||||
Soluzione. Proiezione della superficie S su | ||||||||||||||||||||||||||||||
il piano xOy è il rettangolo S xy, | ||||||||||||||||||||||||||||||
definito dalle disuguaglianze 0 ≤ x ≤ 1, | ||||||||||||||||||||||||||||||
0 ≤ y ≤ 4 . Proiezione della superficie S su | ||||||||||||||||||||||||||||||
il piano yOz è un rettangolo | S yz, definita dalle disuguaglianze |
|||||||||||||||||||||||||||||
0  z  1,0  y  4. Poiché il piano S è perpendicolare al piano |
||||||||||||||||||||||||||||||
xOz , allora ∫∫ ydxdz = 0. Allora, per le formule (4.7) e (4.9) abbiamo |
||||||||||||||||||||||||||||||
∫∫ xdydz+ ydxdz+ zdxdy= ∫∫ (1 − z) dydz+ |
||||||||||||||||||||||||||||||
S yz | ||||||||||||||||||||||||||||||
+ ∫∫ (1 − x) dxdy= ∫ dy∫ (1 − z) dz+ ∫ dy∫ (1 − x) dx= |
||||||||||||||||||||||||||||||
Sxy | ||||||||||||||||||||||||||||||
−z) | (1− x) | |||||||||||||||||||||||||||||
2 ∫ | di = 4. |
|||||||||||||||||||||||||||||
= ∫dy− | + ∫ dy − | |||||||||||||||||||||||||||||
4.4. Formula di Ostrogradskij. La formula di Ostrogradsky stabilisce una connessione tra l'integrale di superficie su una superficie chiusa e l'integrale triplo sulla regione spaziale limitata da questa superficie.
Sia V una regione regolare chiusa delimitata dalla superficie S, e siano le funzioni P(x, y, z), Q(x, y, z), R(x, y, z)
sono continui insieme alle loro derivate parziali del primo ordine in una data regione. Allora vale la seguente formula:
∫∫∫( | ∂P | ∂Q | ∂ R ) dxdydz= ∫∫ Pdydz+ Qdxdz+ Rdxdy, (4.10) |
|||
∂x | ∂y | ∂z | ||||
chiamato La formula di Ostrogradskij 1 .
Utilizzando la formula di Ostrogradsky è conveniente calcolare gli integrali di superficie su superfici chiuse.
Esempio 4.4. Usando la formula di Ostrogradsky, calcola
∫∫ xdydz + ydxdz + zdxdy , | Dove S | ||||||||||||||||||||||||||
lato della piramide | limitato | aerei | |||||||||||||||||||||||||
X + sì + z = 1, | X= 0,sì= 0, | z= 0 (Fig. 4.5). | |||||||||||||||||||||||||
Secondo | |||||||||||||||||||||||||||
Ostrogradskij: | |||||||||||||||||||||||||||
P(X,sì,z)= X,Q(X,sì,z)= sì,R(X,sì,z)= z. | |||||||||||||||||||||||||||
Poi: ∂ P+ | ∂ Q+ | ∂R | = 1+ 1+ 1= 3,e troviamo | ||||||||||||||||||||||||
∂X | ∂sì | ∂z | |||||||||||||||||||||||||
1− X | 1 −X−sì | ||||||||||||||||||||||||||
∫∫ xdydz + ydxdz + zdxdy = 3 ∫∫∫ dxdydz = 3 ∫ dx ∫ dy | ∫ dz = | ||||||||||||||||||||||||||
1− X | 1 −X−sì | 1− X | |||||||||||||||||||||||||
= 3 ∫ dx ∫ dy ∫ dz = 3 ∫ dx ∫ (1 − X − sì ) dy = | |||||||||||||||||||||||||||
sì 2 | 1− X | ||||||||||||||||||||||||||
3 ∫ dx ( sì − xy − | |||||||||||||||||||||||||||
−2 X+1 | 3 (X− 1) | ||||||||||||||||||||||||||
= 3 ∫ (1 −X−X+X2 − | ) dx = | ∫ ( X − 1) 2 dx = | |||||||||||||||||||||||||
Osservazione 4.1. La connessione tra integrali di superficie del primo e del secondo tipo è simile alla connessione tra integrali curvilinei:
∫∫ F ( X , sì , z ) dxdy = ∫∫ F ( X , sì , z )cosα ds ,
∫∫ F ( X , sì , z ) dydz = ∫∫ F ( X , sì , z )cosβ ds ,
∫∫ F ( X , sì , z ) dxdz = ∫∫ F ( X , sì , z )cosγ ds ,
Dove cosα ,cosβ ,cosγ - direzione coseni della normale corrispondente a
lato selezionato della superficie. ,sì) | continuativo sul territorio Sxy– proiezioni superficiali S |
||||||||||||||||||||||
all'aereo xOy;l | – contorno, | limitante | superficie | S ; l – |
|||||||||||||||||||
proiezione della linea spaziale l all'aereo | xOy , | essendo |
|||||||||||||||||||||
un canile che delimita l'area D. Selezioniamo il lato superiore |
|||||||||||||||||||||||
superfici S. Se le funzioni P(X, sì, z), Q(X, sì, z), R(X, sì, z) | continuo |
||||||||||||||||||||||
insieme alle sue derivate parziali del primo ordine su |
|||||||||||||||||||||||
superfici S, allora vale la seguente formula: | |||||||||||||||||||||||
∫ Pdx + Qdy + Rdz = | |||||||||||||||||||||||
= ∫∫ | (∂ Q | ∂ P) dxdy + ( | ∂R | ∂ Q) dydz + (∂ P | ∂ R) dxdz | ||||||||||||||||||
∂X | ∂sì | ∂sì | ∂z | ∂z | ∂X | ||||||||||||||||||
(l- si muove in una direzione positiva) | chiamato formula |
||||||||||||||||||||||
Se come superficie S prendere l'area D in superficie xOy |
|||||||||||||||||||||||
(z= 0 ), allora dalla (4.11) si ottiene la formula di Green | ∂Q | ∂ P) dxdy . | |||||||||||||||||||||
∫ P ( X , sì ) dx + Q ( X , sì ) dy = ∫∫ ( | |||||||||||||||||||||||
∂X | ∂sì | ||||||||||||||||||||||
Pertanto, la formula di Green è un caso speciale della formula di Stokes. |
|||||||||||||||||||||||
Si noti che l'integrale di superficie della formula è del secondo tipo |
|||||||||||||||||||||||
Stokes (4.11) può essere sostituito dall'integrale di superficie del primo |
|||||||||||||||||||||||
tipo. Quindi questa formula prenderà la forma | |||||||||||||||||||||||
∫ Pdx + Qdy + Rdz = | |||||||||||||||||||||||
∂Q | ∂P | ∂R | ∂Q | ∂P | ∂R | ||||||||||||||||||
= ∫∫ | )cos α + ( | )cos β + ( | )cos γ | ||||||||||||||||||||
∂X | ∂sì | ∂sì | ∂z | ∂z | ∂X | ds , | |||||||||||||||||
Dove cos α ,così β ,così γ , | Significare | guide | coseni | ||||||||||||||||||||
corrispondente al lato selezionato della superficie. | |||||||||||||||||||||||
utilizzando la formula | calcolare |
||||||||||||||||||||||
∫ X 2 sì 3 dx + dy + zdz , | cerchio, | dato dalle equazioni |
|||||||||||||||||||||
X 2 + sì 2 + 1, z = 0 . | Superficie S serve il lato superiore dell'emisfero |
||||||||||||||||||||||
X 2+ sì 2+ z 2= 1, | z> 0 (l va in una direzione positiva). |
||||||||||||||||||||||
Per i casi in cui l'integrazione avviene non su un segmento di curva, ma su una superficie delimitata. Come gli integrali curvilinei, gli integrali di superficie sono del primo e del secondo tipo.
Integrale di superficie di prima specie scritto nel modulo
Dove F(M) = F(x,y,z) è una funzione di tre variabili e la superficie σ - area di integrazione di questa funzione. Se F(x,y,z) è uguale all'unità, allora l'integrale di superficie è uguale alla superficie.
Immagina un girasole abbastanza grande con semi molto, molto piccoli. Quindi, dalla somma delle superfici di semi molto, molto piccoli situati sulla superficie di un girasole, si può calcolare la superficie del girasole: questa potrebbe essere un'interpretazione semplificata dell'integrale di superficie. Perché?
Passiamo ad una definizione più formale di integrale di superficie. Superficie σ diviso in N parti con aree Δ σ 1 , Δ σ 2 , ..., Δ σ N. Se selezioni un punto arbitrario su ciascuna superficie parziale (seme) Mio con coordinate ( ζ io, η io, ς io ,), allora possiamo tirare le somme
Questa somma è chiamata somma integrale della funzione F(M) sulla superficie σ . Ora massimizzeremo il numero di parti così piccole e il diametro maggiore Δ σ io- al contrario, ridurre. Se la somma integrale come il maggiore dei diametri delle parti tende a zero (cioè, come abbiamo già notato, tutte le parti sono molto piccole) ha un limite, allora questo limite si chiama integrale di superficie di prima specie dalla funzione F(M) sulla superficie σ .
Calcolo dell'integrale di superficie di prima specie
Lascia che la superficie σ dato dall'equazione z = z(X, sì) , la sua proiezione sul piano xOyè la zona Dxy, mentre la funzione z = z(X, sì) e le sue derivate parziali sono continue nella regione Dxy.
Esempio 1.
Dove σ - parte dell'aereo nel primo ottante.
Soluzione. Disegno:
Dall’equazione del piano si ottiene l’espressione “zet”: 
.
Allora le derivate parziali sono: , e
.
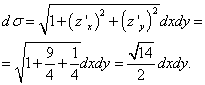Superficie σ è il triangolo mostrato nel disegno ABC e la sua proiezione sul piano xOy- triangolo AOB, che è limitato da linee rette X = 0 , sì= 0 e 3 X + sì= 6. Passiamo dall’integrale di superficie all’integrale doppio e risolviamolo:
.
Il concetto di integrale di superficie del secondo tipo
Prima di passare alla definizione di integrale di superficie del secondo tipo è necessario familiarizzare con i concetti di lati di superfici e superfici orientate.
Sia data nello spazio una superficie liscia σ . Scegliamo un punto arbitrario su questa superficie M e disegna attraverso di esso il vettore normale alla superficie. Attraverso il punto M effettueremo anche in superficie σ un contorno arbitrario che non ha punti in comune con il confine della superficie σ . Punto M insieme al vettore normale ci sposteremo lungo il contorno in modo che il vettore normale sia costantemente perpendicolare alla superficie σ . Alla restituzione del punto M rispetto alla posizione iniziale sono possibili due casi: la direzione del vettore normale rimarrà la stessa oppure cambierà in senso opposto.
Se la direzione del vettore normale non cambia, allora la superficie σ detto bilaterale. Se, durante l'attraversamento del contorno, la direzione del vettore normale cambia in senso opposto, la superficie viene chiamata unilaterale. Le superfici a due lati sono chiamate superfici orientate, le superfici a un lato sono chiamate superfici non orientate.
Un esempio di superficie unilaterale è un nastro di Möbius (nella foto sopra), che può essere realizzato da una striscia di carta con un lato ruotato di 180 gradi e poi le estremità incollate insieme. Ed ecco cosa è importante qui: per una superficie unilaterale non viene introdotto il concetto di integrale di superficie del secondo tipo .
Quindi considereremo solo le superfici a due lati. Esempi di superfici a due lati sono piani, sfere, ellissoidi e paraboloidi.
Il lato positivo di una superficie a due lati determina la direzione del vettore normale. Il lato opposto della superficie è detto negativo. Il lato positivo di una superficie è il suo lato superiore. Se i vettori normali alle unità formano angoli acuti con l'asse Oz, viene selezionato il lato superiore della superficie z = z(X, sì) , se gli angoli sono ottusi, allora il lato inferiore della superficie.
Come nel caso dell'integrale di superficie del primo tipo, la superficie può essere suddivisa in N parti. Nel formulare il concetto di integrale di superficie del primo tipo, la somma integrale comprendeva le aree di ciascuna delle parti per le quali venivano moltiplicati i valori della funzione F(Mio). Nel caso di un integrale di superficie del secondo tipo non si prendono le aree delle parti stesse, ma le aree delle loro proiezioni sui piani coordinati . E per distinguere la funzione di tre variabili da un integrale del primo tipo denotiamo R(X,sì,z) . Quindi la somma integrale verrà scritta come segue:
,
dove Δ Sio- le aree delle citate proiezioni di parti del lato della superficie sull'asse delle coordinate (per ora assumeremo che sull'asse xOy).
Con tali convenzioni e notazioni, la definizione di integrale di superficie del secondo tipo è simile alla definizione di integrale del primo tipo. Vale a dire: un integrale di superficie del secondo tipo è il limite di una data somma integrale poiché il diametro maggiore delle parti della superficie considerata tende a zero.
E' scritto così:
.
In questo caso la funzione R(X,sì,z) integrabile su variabili X E sì, poiché parti della superficie venivano proiettate sul piano xOy.
Allo stesso modo possiamo scrivere altri due integrali di superficie del secondo tipo:
(funzione P(X,sì,z) integrabile su variabili sì E z yOz),
(funzione Q(X,sì,z) integrabile su variabili z E X, poiché parti della superficie vengono proiettate sul piano zOx).
La somma di questi integrali
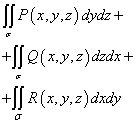
chiamato integrale di superficie generale di seconda specie ed è designato
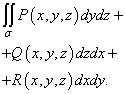
Calcolo dell'integrale di superficie di seconda specie
Un integrale di superficie del secondo tipo si calcola scomponendo l'integrale di superficie generale del secondo tipo nella somma degli integrali di superficie (vedi fine del paragrafo precedente) e riducendo ciascuno di essi ad un integrale doppio.
Consideriamo in dettaglio il calcolo dell'integrale
.
Lascia che la superficie σ dato dall'equazione z = z(X, sì) . Indichiamo il lato positivo della superficie, il lato negativo e la proiezione sul piano xOy - Dxy.
Otteniamo così una formula per calcolare l'integrale di superficie del secondo tipo:
Se viene selezionato il lato negativo della superficie, il segno dell'integrale cambia:
Gli altri due integrali separati - termini di quello generale - si calcolano in modo simile:
Esempio 2.
,
Dove σ - il lato superiore di una parte dell'aereo, tagliato dagli aerei sì= 0 e sì= 4 e situato nel primo ottante.
Soluzione. Il disegno è nella foto sopra. Per definizione, otteniamo la somma di tre integrali doppi:
Il secondo integrale è uguale a zero, essendo il piano σ parallelo all'asse Ehi. Troviamo quindi il primo ed il terzo integrale:
Non resta che sommare tutti gli integrali individuali e ottenere l’integrale di superficie generale della seconda specie:
.
Se devi calcolare un integrale di superficie del secondo tipo su una superficie chiusa, puoi andare a triplo integrale, utilizzando la formula di Ostrogradsky. Quindi, se le funzioni P(x,y,z) , Q(x,y,z) E R(x,y,z) e le loro derivate parziali , , sono funzioni continue nel dominio W, che è delimitato da una superficie chiusa σ , quindi quando si integra all'esterno della superficie, l'uguaglianza
Esempio 3. Calcolare l'integrale di superficie del secondo tipo
,
Dove σ - il lato esterno della superficie di un cono formato da una superficie e da un piano z = 2 .
Soluzione. Questa superficie è la superficie di un cono con un raggio R= 2 e altezza H= 2. Questa è una superficie chiusa, quindi puoi usare la formula di Ostrogradsky. Perché P = 3X , Q = 4sì , R = −z, quindi le derivate parziali , , .
Passiamo all'integrale triplo, che risolviamo:
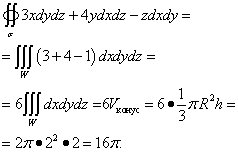
Altri esempi sul calcolo degli integrali di superficie
Esempio 4. Calcolare l'integrale di superficie del primo tipo
Dove σ - superficie laterale del cono a .
Soluzione. A partire dalle derivate parziali 
,
, Quello
Riduciamo questo integrale di superficie ad uno doppio:
Proiezione di una superficie su un piano xOyè una circonferenza con centro nell'origine e raggio R= 2, quindi, quando calcoliamo l'integrale doppio, passiamo al sistema di coordinate polari. Per fare ciò, cambiamo le variabili:
Otteniamo il seguente integrale, che infine risolviamo:
Esempio 5. Calcolare l'integrale di superficie del secondo tipo
,
Dove σ - la parte superiore del triangolo formato dall'intersezione del piano con i piani coordinati.
Soluzione. Dividiamo questo integrale di superficie per la somma di due integrali
, Dove
.
Per calcolare l'integrale IO1 σ all'aereo yOz. La proiezione è un triangolo OCB, che è sull'aereo yOz limitare le linee rette o, sì= 0 e z= 0. Dall'equazione del piano si deriva. Possiamo quindi calcolare l'integrale IO1 :
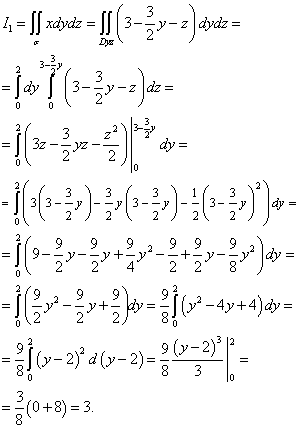
Per calcolare l'integrale IO2 , costruiamo una proiezione di superficie σ all'aereo zOx. La proiezione è un triangolo AOC, che è delimitato da linee rette o , X= 0 e z= 0. Calcoliamo:
Sommiamo i due integrali risultanti e infine otteniamo questo integrale di superficie:
.
Esempio 6. Calcolare l'integrale di superficie del secondo tipo
,
Dove σ
- la superficie esterna di una piramide formata da un piano 
e coordinare i piani.
Esempio 3.3. Calcolare il lavoro di un campo vettoriale
UN = 2X 2 sì io – xy 2 J
dall'origine O al punto A(1;1), se lo spostamento avviene lungo: UN) segmento; B) archi di parabola; V) linea spezzata OBA, dove B(1;0) (vedi Fig. 3.1).
Soluzione . UN) L'equazione della retta OA ha la forma y=x. Permettere x=t, allora l'equazione della retta in forma parametrica assumerà la forma:
x=t, y=t,
e quando ci si sposta da A a B il parametro T cambierà da 0 a 1. Quindi il lavoro svolto sarà uguale a
B) Permettere x=t 2 , y=t, Poi
x=t 2 , y=t, 0£ T£ 1 .
.
V) L'equazione della retta (OB) è sì=0 (0£ X£ 1); l'equazione della retta (BA) ha la forma X=1 (0£ sì£ 1). Poi
, 
.
Di conseguenza, otteniamo,
.
Commento. Se nel caso di campi bidimensionali l'equazione della linea è descritta dall'equazione sì=sì(X), e la variabile x varia da UN Prima B, allora l'integrale curvilineo del 2° sarà calcolato con la formula:
. (3.9)
L'esempio precedente potrebbe essere risolto utilizzando questa formula senza introdurre il parametro T.
Esempio 3.4. Calcola l'integrale
,
dove L è l'arco della parabola y=x 2 +1 dal punto A(0;1) al punto B(2;5).
Soluzione . Facciamo un disegno (vedi Fig. 3.2). Dall'equazione della parabola otteniamo y"=2x. Poiché sull'arco di una parabola AB variabile X cambia da 0 a 2, allora l'integrale curvilineo, secondo la formula (3.9), assumerà la forma
4. INTEGRALI DI SUPERFICIE
4.1. Integrali di superficie di prima specie
L'integrale di superficie del 1° tipo è una generalizzazione dell'integrale doppio e si introduce in modo simile. Considera una superficie S, liscio o liscio a tratti, e assumiamo che la funzione f( x,y,z) è definita e limitata su questa superficie. Dividiamo questa superficie in N parti arbitrarie. L'area di ciascun appezzamento è indicata con D sì io. Su ogni sezione selezioniamo un punto con coordinate ( x io, y io, z io) e calcolare il valore della funzione in ciascuno di questi punti. Successivamente, creiamo la somma integrale:
.
Se esiste un limite di somme integrali a N®¥ (in questo caso max D sì io®0), cioè tale limite non dipende né dal metodo di partizionamento né dalla scelta dei punti medi, quindi tale limite si chiama integrale di superficie di prima specie :
. (4.1)
Se la funzione f( x,y,z) è continua sulla superficie S, allora esiste il limite (4.1).
Se la funzione integranda f( x,y,z)º1, allora l'integrale di superficie di 1a specie è uguale alla superficie S:
. (4.2)
Supponiamo che venga introdotto un sistema di coordinate cartesiane e qualsiasi linea retta parallela all'asse Oz, può attraversare la superficie S solo ad un certo punto. Quindi l'equazione della superficie S può essere scritto nella forma
z = z(x,y)
ed è proiettato in modo univoco sull'aereo xOy. Di conseguenza, l'integrale di superficie del 1° tipo può essere espresso in termini di integrale doppio
.
(4.3)
Esempio 4.1. Calcola l'integrale
,
Dove S– parte della superficie conica z 2 =X 2 +sì£ 2,0 z£ 1.
Soluzione. Abbiamo
Quindi l'integrale richiesto viene trasformato in un integrale doppio
Dove Sxy- cerchio X 2 +sì 2 £ 1. Ecco perché
.
4.2. Integrali di superficie di seconda specie
Lascia che un campo vettoriale venga specificato in qualche regione
UN = ascia io + Ay J + una z K
e qualsiasi superficie bifacciale S. Dividiamo in qualche modo la superficie in aree elementari D S i. Su ogni sito scegliamo un punto arbitrario P io e comporre la somma integrale:
, (4.4)
Dove N (P i) – vettore normale ad una data superficie in un punto P i. Se esiste un limite a tale somma ai sensi del D S i®0, allora viene chiamato questo limite integrale di superficie di 2a specie (O fluire campo vettoriale UN attraverso la superficie S) ed è indicato dal simbolo
O ,
Dove D S =N ds.
Poiché il vettore normale unitario ha i coseni direzionali come coordinate N =(cosa, cosb, cosg). Quello
Pertanto, il calcolo degli integrali di superficie del 2° tipo può essere ridotto al calcolo degli integrali di superficie del 1° tipo. Tuttavia, cosa A differenza degli integrali di superficie del 1° tipo, gli integrali del 2° tipo dipendono dalla scelta del lato della superficie. La transizione verso l'altro lato della superficie modifica la direzione della normale alla superficie e, di conseguenza, il segno dell'integrale.
Consideriamo l'integrale
.
Lascia che l'equazione della superficie abbia la forma z=j( x,y) e il lato positivo di questa superficie sarà considerato quello la cui normale si forma con l'asse O z angolo acuto. Poi
cosg ds = dxdy.
Pertanto, l'integrale in esame può essere scritto nella forma
.
Sostituzione z da j( x,y), arriviamo all’integrale doppio
,
Dove Sxy– proiezione della superficie S all'aereo xOy.
