Formula per il calcolo della mediana nelle statistiche. Caratteristiche strutturali delle serie di distribuzione delle variazioni

TEST

Sull'argomento: "Modalità. Mediana. Metodi per il loro calcolo"

introduzione

I valori medi e gli indicatori di variazione associati svolgono un ruolo molto importante nelle statistiche, dovuto all'oggetto del suo studio. Pertanto, questo argomento è uno dei centrali del corso.

La media è una misura riassuntiva molto comune nelle statistiche. Ciò si spiega con il fatto che solo con l'aiuto della media una popolazione può essere caratterizzata da una caratteristica quantitativamente variabile. In statistica, il valore medio è una caratteristica generalizzante di un insieme di fenomeni simili basata su alcune caratteristiche quantitativamente variabili. La media mostra il livello di questa caratteristica per unità di popolazione.

Quando studiano i fenomeni sociali e cercano di identificarne le caratteristiche, i tratti tipici in condizioni specifiche di luogo e tempo, gli statistici utilizzano ampiamente i valori medi. Usando le medie, puoi confrontare diverse popolazioni tra loro in base a caratteristiche diverse.

Le medie utilizzate nelle statistiche appartengono alla classe delle medie di potenza. Tra le medie di potenza, viene utilizzata più spesso la media aritmetica, meno spesso la media armonica; La media armonica viene utilizzata solo quando si calcolano i tassi medi della dinamica e il quadrato medio viene utilizzato solo quando si calcolano gli indici di variazione.

La media aritmetica è il quoziente di divisione della somma delle varianti per il loro numero. Viene utilizzato nei casi in cui il volume di una caratteristica variabile per l'intera popolazione è formato dalla somma dei valori caratteristici delle sue singole unità. La media aritmetica è il tipo più comune di media, poiché corrisponde alla natura dei fenomeni sociali, dove il volume delle caratteristiche variabili nell'aggregato è spesso formato proprio come la somma dei valori caratteristici delle singole unità della popolazione .

Secondo la sua proprietà distintiva, la media armonica dovrebbe essere utilizzata quando il volume totale dell'attributo è formato come somma dei valori inversi della variante. Si utilizza quando, a seconda del materiale, i pesi non devono essere moltiplicati, ma divisi in opzioni o, che è la stessa cosa, moltiplicati per il loro valore reciproco. La media armonica in questi casi è il reciproco della media aritmetica dei valori reciproci della caratteristica.

Si dovrebbe ricorrere alla media armonica nei casi in cui come pesi non vengono utilizzate le unità della popolazione - i portatori della caratteristica, ma i prodotti di queste unità per il valore della caratteristica.

1. Definizione di moda e mediana in statistica

Le medie aritmetiche e armoniche generalizzano le caratteristiche della popolazione secondo l'una o l'altra caratteristica variabile. Le caratteristiche descrittive ausiliarie della distribuzione di una caratteristica variabile sono la moda e la mediana.

In statistica, una moda è il valore di una caratteristica (variante) che si riscontra più spesso in una determinata popolazione. In una serie di variazioni, questa sarà l'opzione con la frequenza più alta.

Nelle statistiche, la mediana è l'opzione che si trova al centro della serie di variazioni. La mediana divide la serie a metà; su entrambi i lati di essa (sopra e sotto) si trova lo stesso numero di unità di popolazione.

Moda e mediana, a differenza delle medie di potenza, sono caratteristiche specifiche; il loro significato è assegnato a qualsiasi opzione specifica nella serie di variazioni.

La modalità viene utilizzata nei casi in cui è necessario caratterizzare il valore che ricorre più frequentemente di una caratteristica. Se è necessario, ad esempio, scoprire il tasso salariale più comune in un'impresa, il prezzo sul mercato al quale è stata venduta la maggior quantità di beni, il numero di scarpe più richiesto dai consumatori, ecc., in in questi casi ricorrono alla moda.

La mediana è interessante in quanto mostra il limite quantitativo del valore di una caratteristica variabile, raggiunto dalla metà dei membri della popolazione. Lascia che lo stipendio medio dei dipendenti della banca sia di 650.000 rubli. al mese. Questa caratteristica può essere completata se diciamo che la metà dei lavoratori riceveva uno stipendio di 700.000 rubli. e superiore, cioè Diamo la mediana. La moda e la mediana sono caratteristiche tipiche nei casi in cui le popolazioni sono omogenee e numerose.

2. Trovare la moda e la mediana in una serie a variazioni discrete

Trovare la moda e la mediana in una serie di variazioni, dove i valori di una caratteristica sono dati da determinati numeri, non è molto difficile. Consideriamo la Tabella 1 con la distribuzione delle famiglie per numero di figli.

Tabella 1. Distribuzione delle famiglie per numero di figli

Ovviamente, in questo esempio, la moda sarà una famiglia con due figli, poiché questo valore di opzione corrisponde al maggior numero di famiglie. Potrebbero esserci distribuzioni in cui tutte le opzioni si verificano con la stessa frequenza, nel qual caso non esiste una modalità o, in altre parole, possiamo dire che tutte le opzioni sono ugualmente modali. In altri casi, non una, ma due opzioni potrebbero avere la frequenza più alta. Poi ci saranno due modalità, la distribuzione sarà bimodale. Le distribuzioni bimodali possono indicare un'eterogeneità qualitativa della popolazione in base alla caratteristica studiata.

Per trovare la mediana in una serie di variazioni discrete, è necessario dividere la somma delle frequenze a metà e aggiungere ½ al risultato. Quindi, nella distribuzione di 185 famiglie per il numero di figli, la mediana sarà: 185/2 + ½ = 93, cioè La 93a opzione, che divide a metà la riga ordinata. Qual è il significato della 93a opzione? Per scoprirlo è necessario accumulare frequenze, partendo dalle opzioni più piccole. La somma delle frequenze della 1a e della 2a opzione è 40. È chiaro che qui non ci sono 93 opzioni. Se sommiamo la frequenza della 3a opzione a 40, otteniamo una somma pari a 40 + 75 = 115. Pertanto la 93a opzione corrisponde al terzo valore della caratteristica variabile, e la mediana sarà una famiglia con due figli.

La moda e la mediana in questo esempio coincidono. Se avessimo una somma pari di frequenze (ad esempio, 184), quindi, utilizzando la formula sopra, otterremmo il numero dell'opzione mediana, 184/2 + ½ = 92,5. Poiché non sono presenti opzioni frazionarie, il risultato indica che la mediana è a metà strada tra 92 e 93 opzioni.

3. Calcolo della moda e della mediana nelle serie a variazione di intervallo

La natura descrittiva della moda e della mediana è dovuta al fatto che non compensano le deviazioni individuali. Corrispondono sempre a un'opzione specifica. Pertanto, la moda e la mediana non richiedono calcoli per verificare se tutti i valori dell'attributo sono noti. Tuttavia, in una serie di variazioni di intervallo, i calcoli vengono utilizzati per trovare il valore approssimativo della moda e della mediana entro un determinato intervallo.

Per calcolare un certo valore del valore modale di una caratteristica contenuta in un intervallo, utilizzare la formula:

M o = X Mo + i Mo *(f Mo – f Mo-1)/((f Mo – f Mo-1) + (f Mo – f Mo+1)),

Dove XMo è il limite minimo dell'intervallo modale;

i Mo – il valore dell'intervallo modale;

f Mo – frequenza dell'intervallo modale;

f Mo-1 – frequenza dell'intervallo precedente quello modale;

f Mo+1 – frequenza dell'intervallo successivo a quello modale.

Mostriamo il calcolo della moda utilizzando l'esempio riportato nella Tabella 2.

Tabella 2. Distribuzione degli occupati delle imprese per rispetto degli standard produttivi

Per trovare la moda, determiniamo innanzitutto l'intervallo modale di questa serie. L'esempio mostra che la frequenza più alta corrisponde all'intervallo in cui le varianti si trovano nell'intervallo da 100 a 105. Questo è l'intervallo modale. Il valore dell'intervallo modale è 5.

Sostituendo i valori numerici della Tabella 2 nella formula sopra, otteniamo:

M o = 100 + 5 * (104 -12)/((104 – 12) + (104 – 98)) = 108,8

Il significato di questa formula è il seguente: il valore di quella parte dell'intervallo modale che deve essere aggiunta al suo limite minimo è determinato in base all'entità delle frequenze degli intervalli precedente e successivo. In questo caso aggiungiamo 8,8 a 100, cioè più di metà intervallo perché la frequenza dell'intervallo precedente è inferiore alla frequenza dell'intervallo successivo.

Calcoliamo ora la mediana. Per trovare la mediana in una serie di variazioni di intervallo, determiniamo innanzitutto l'intervallo in cui si trova (intervallo mediano). Tale intervallo sarà quello la cui frequenza cumulativa è pari o superiore alla metà della somma delle frequenze. Le frequenze cumulative si formano sommando gradualmente le frequenze, a partire dall'intervallo con il valore più basso dell'attributo. La metà della somma delle frequenze è 250 (500:2). Pertanto, secondo la tabella 3, l'intervallo mediano sarà l'intervallo con un valore salariale di 350.000 rubli. fino a 400.000 rubli.

Tabella 3. Calcolo della mediana nelle serie di variazioni di intervallo

Prima di questo intervallo la somma delle frequenze accumulate era 160. Pertanto per ottenere il valore mediano è necessario aggiungere altre 90 unità (250 – 160).

Mediano Me chiamano il valore dell'attributo che cade al centro della serie classificata e lo dividono in due parti uguali in numero di unità. Pertanto, nella riga classificata della distribuzione, metà della riga ha valori degli attributi superiori alla mediana, l'altra metà è inferiore alla mediana.

La mediana viene utilizzata al posto della media aritmetica quando le opzioni estreme della serie classificata (la più piccola e la più grande) rispetto al resto risultano essere eccessivamente grandi o eccessivamente piccole.

IN discreto in una serie di variazioni contenente un numero dispari di unità, la mediana è uguale alla variante della caratteristica che ha il numero:
,
dove N è il numero di unità di popolazione.
In una serie discreta composta da un numero pari di unità di popolazione, la mediana è definita come la media delle opzioni aventi numeri e:
.
Nella distribuzione dei lavoratori per anzianità di servizio, la mediana è pari alla media delle opzioni aventi numero 10 nella serie classificata: 2 = 5 e 10: 2 + 1 = 6. Le opzioni per la quinta e la sesta caratteristica sono uguali a 4 anni, quindi
dell'anno
Quando si calcola la mediana in intervallo prima riga trova intervallo mediano, (cioè contenente la mediana), per il quale vengono utilizzate frequenze o frequenze accumulate. La mediana è un intervallo la cui frequenza accumulata è pari o superiore alla metà del volume totale della popolazione. Il valore mediano viene quindi calcolato utilizzando la formula:
,
dov'è il limite inferiore dell'intervallo mediano;
– larghezza dell'intervallo mediano;
– frequenza cumulativa dell'intervallo precedente la mediana;
– frequenza dell'intervallo mediano.
Calcoliamo la mediana della distribuzione dei lavoratori per stipendio (vedi lezione “Riepilogo e raggruppamento dei dati statistici”).
La mediana è la fascia salariale di 800-900 UAH, poiché la sua frequenza cumulativa è 17, che supera la metà della somma di tutte le frequenze (). Poi
Io=800+100 UAH.
Il valore ottenuto indica che la metà dei lavoratori ha un salario inferiore a 875 UAH, ma questo è superiore alla media.
Per determinare la mediana, è possibile utilizzare le frequenze cumulative anziché le frequenze cumulative.
La mediana, come la moda, non dipende dai valori estremi della variante, pertanto viene utilizzata anche per caratterizzare il centro in serie distributive a confini incerti.
Proprietà mediana : la somma dei valori assoluti delle deviazioni dalla mediana è inferiore a qualsiasi altro valore (anche dalla media aritmetica):

Questa proprietà della mediana viene utilizzata nei trasporti quando si progetta l'ubicazione delle fermate del tram e del filobus, delle stazioni di servizio, dei punti di raccolta, ecc.
Esempio. Ci sono 10 garage lungo l'autostrada lunga 100 km. Per progettare la costruzione di una stazione di servizio, sono stati raccolti dati sul numero di viaggi previsti alla stazione di servizio per ciascun garage.
Tabella 2 - Dati sul numero di spostamenti ai distributori di benzina per ciascuna autorimessa.

È necessario installare una stazione di servizio in modo che il chilometraggio totale dei veicoli per il rifornimento sia minimo.
Opzione 1. Se una stazione di servizio si trova al centro dell'autostrada, ad es. al 50esimo chilometro (il centro dell'intervallo di modifiche nell'attributo), il chilometraggio, tenendo conto del numero di viaggi, sarà:
a) in una direzione:
;
b) al contrario:
;
c) chilometraggio totale in entrambe le direzioni: .

Opzione 2. Se una stazione di servizio si trova nel tratto centrale dell'autostrada, determinata con la formula della media aritmetica, tenendo conto del numero di viaggi:

La mediana può essere determinata graficamente, utilizzando il cumulo (vedi lezione “Riepilogo e raggruppamento dei dati statistici”). Per fare ciò, l'ultima ordinata, pari alla somma di tutte le frequenze o frequenze, viene divisa a metà. Dal punto risultante si ripristina una perpendicolare fino all'intersezione con il cumulo. L'ascissa del punto di intersezione dà il valore mediano.

La funzione MEDIANA in Excel viene utilizzata per analizzare un intervallo di valori numerici e restituisce un numero che è il centro dell'insieme esaminato (la mediana). Cioè, questa funzione divide condizionatamente un insieme di numeri in due sottoinsiemi, il primo dei quali contiene numeri inferiori alla media e il secondo maggiore. La mediana è uno dei numerosi metodi per determinare la tendenza centrale di un intervallo di interesse.

Esempi di utilizzo della funzione MEDIANA in Excel

Quando si studiavano le fasce d'età degli studenti, sono stati utilizzati i dati di un gruppo di studenti selezionati casualmente in un'università. Il compito è determinare l'età media degli studenti.

Dati iniziali:

Formula per il calcolo:

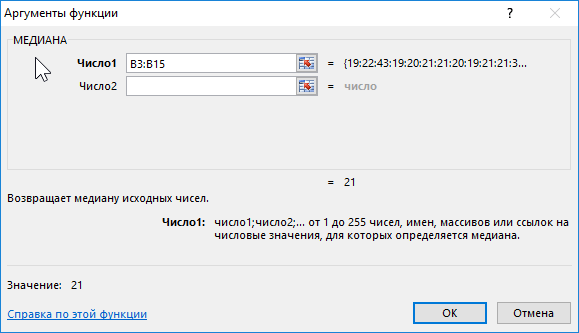
Descrizione dell'argomento:

• B3:B15 – fascia di età studiata.

Risultato:

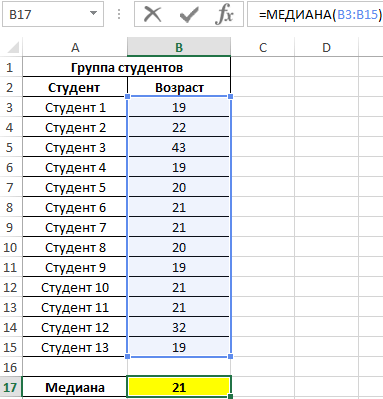
Cioè, nel gruppo ci sono studenti la cui età è inferiore a 21 anni e superiore a questo valore.



Confronto tra le funzioni MEDIANA e MEDIA per il calcolo del valore medio

Durante i giri serali in ospedale è stata misurata la temperatura corporea di ogni paziente. Dimostrare l'utilità di utilizzare il parametro mediano invece del valore medio per esaminare un intervallo di valori ottenuti.

Dati iniziali:

Formula per trovare la media:

Formula per trovare la mediana:

Come si può vedere dal valore medio, in media la temperatura dei pazienti è più alta del normale, ma questo non è vero. La mediana mostra che almeno la metà dei pazienti ha una temperatura corporea normale, non superiore a 36,6.

Attenzione! Un altro metodo per determinare la tendenza centrale è la moda (il valore più frequente nell'intervallo studiato). Per determinare la tendenza centrale in Excel, è necessario utilizzare la funzione MODALITÀ. Tieni presente che in questo esempio i valori della mediana e della moda sono gli stessi:

Cioè, il valore mediano che divide un insieme in sottoinsiemi di valori più piccoli e più grandi è anche il valore che ricorre più frequentemente nell'insieme. Come puoi vedere, la maggior parte dei pazienti ha una temperatura di 36,6.

Un esempio di calcolo della mediana nell'analisi statistica in Excel

Esempio 3. Ci sono 3 venditori che lavorano in un negozio. Sulla base dei risultati degli ultimi 10 giorni è necessario determinare il dipendente a cui verrà riconosciuto il bonus. Quando si sceglie il miglior dipendente, viene preso in considerazione il grado di efficienza del suo lavoro e non il numero di beni venduti.

Tabella dati originale:

Per caratterizzare l'efficienza, utilizzeremo tre indicatori contemporaneamente: valore medio, mediana e moda. Determiniamoli per ciascun dipendente utilizzando rispettivamente le formule MEDIA, MEDIANA e MODA:

Per determinare il grado di dispersione dei dati, utilizziamo un valore che è il valore totale del modulo della differenza tra valore medio e moda, valore medio e mediana, rispettivamente. Cioè il coefficiente x=|av-med|+|av-mod|, dove:

• av – valore medio;
• med – mediano;
• mod - moda.

Calcoliamo il valore del coefficiente x per il primo venditore:

Effettueremo i calcoli in modo simile per gli altri venditori. Risultati:

Determiniamo il venditore a cui verrà assegnato il bonus:

Nota: la funzione PICCOLO restituisce il primo valore minimo dall'intervallo considerato di valori del coefficiente x.

Il coefficiente x è una certa caratteristica quantitativa della stabilità del lavoro dei venditori, introdotta dall'economista del negozio. Con il suo aiuto è stato possibile determinare l'intervallo con le più piccole deviazioni nei valori. Questo metodo dimostra come tre metodi per determinare la tendenza centrale possano essere utilizzati contemporaneamente per ottenere i risultati più affidabili.

Caratteristiche dell'utilizzo della funzione MEDIANA in Excel

La funzione ha la seguente sintassi:

MEDIANA(numero1; [numero2];...)

Descrizione degli argomenti:

• numero1 è un argomento obbligatorio che caratterizza il primo valore numerico contenuto nell'intervallo in studio;
• [numero2] – secondo opzionale (e argomenti successivi, fino a 255 argomenti in totale), che caratterizza il secondo e i successivi valori dell'intervallo in studio.

Note 1:

1. Quando si eseguono calcoli, è più conveniente trasferire immediatamente l'intero intervallo di valori studiati invece di inserire argomenti in sequenza.
2. Gli argomenti accettati sono dati numerici, nomi contenenti numeri, dati di tipo riferimento e matrici (ad esempio, =MEDIANA((1,2,3,5,7,10))).
3. Quando si calcola la mediana, vengono prese in considerazione le celle contenenti valori vuoti o il valore logico VERO, FALSO, che verranno interpretati rispettivamente come valori numerici 1 e 0. Ad esempio, il risultato dell'esecuzione di una funzione con valori logici negli argomenti (VERO; FALSO) è equivalente al risultato dell'esecuzione con argomenti (1;0) ed è uguale a 0,5.
4. Se uno o più argomenti della funzione accettano valori di testo che non possono essere convertiti in valori numerici o contengono codici di errore, la funzione restituirà il codice di errore #VALORE!.
5. Per determinare la mediana di un campione è possibile utilizzare altre funzioni di Excel: PERCENTILE.IN, QUARTILE.IN, MAX Esempi di utilizzo:

• =PERCENTILE.IN(A1:A10,0.5), poiché per definizione la mediana è il 50° percentile.
• =QUARTILE.SU(A1:A10;2), poiché la mediana è il 2° quartile.
• =ALTA(A1:A9,CONT.(A1:A9)/2), ma solo se il numero di numeri nell'intervallo è un numero dispari.

Note 2:

1. Se nell'intervallo in esame tutti i numeri sono distribuiti simmetricamente attorno alla media, la media aritmetica e la mediana per questo intervallo saranno equivalenti.
2. Con grandi deviazioni dei dati nell'intervallo ("dispersione" dei valori), la mediana riflette meglio la tendenza nella distribuzione dei valori rispetto alla media aritmetica. Un ottimo esempio è l’uso della mediana per determinare il livello reale degli stipendi tra la popolazione di uno stato in cui i funzionari guadagnano un ordine di grandezza superiore rispetto ai cittadini comuni.
3. L'intervallo di valori oggetto di studio può contenere:

• Un numero dispari di numeri. In questo caso, la mediana sarà un singolo numero che divide l'intervallo in due sottoinsiemi di valori rispettivamente più grandi e più piccoli;
• Numero pari di numeri. Quindi la mediana viene calcolata come media aritmetica di due valori numerici che dividono l'insieme nei due sottoinsiemi sopra indicati.

Salari in vari settori dell'economia, temperatura e livelli di precipitazione nello stesso territorio per periodi di tempo comparabili, resa dei raccolti coltivati ​​in diverse regioni geografiche, ecc. Tuttavia, la media non è affatto l'unico indicatore generalizzante - in alcuni casi per una valutazione più accurata un valore adeguato è la mediana. Nelle statistiche, è ampiamente utilizzato come caratteristica descrittiva ausiliaria della distribuzione di una caratteristica in una particolare popolazione. Scopriamo in cosa differisce da quello medio e anche perché è necessario utilizzarlo.

Mediana in statistica: definizione e proprietà

Immagina la seguente situazione: 10 persone lavorano in un'azienda insieme al direttore. I lavoratori ordinari ricevono 1.000 UAH e il loro manager, che è anche il proprietario, riceve 10.000 UAH. Se calcoliamo la media aritmetica, risulta che lo stipendio medio in questa impresa è di 1900 UAH. Questa affermazione sarà vera? Oppure prendiamo questo esempio: nello stesso reparto ospedaliero ci sono nove persone con una temperatura di 36,6 °C e una persona con una temperatura di 41 °C. La media aritmetica in questo caso è pari a: (36,6*9+41)/10 = 37,04 °C. Ma questo non significa che tutti i presenti siano malati. Tutto ciò suggerisce che la media da sola spesso non è sufficiente, ed è per questo che ad essa viene utilizzata in aggiunta la mediana. In statistica, questo indicatore è chiamato l'opzione che si trova esattamente al centro della serie di variazioni ordinate. Se lo calcoliamo per i nostri esempi, otteniamo rispettivamente 1000 UAH. e 36,6 °C. In altre parole, una mediana in statistica è un valore che divide una serie a metà in modo tale che su entrambi i lati di essa (verso il basso o verso l'alto) ci sia lo stesso numero di unità in una data popolazione. A causa di questa proprietà, questo indicatore ha molti altri nomi: 50° percentile o 0,5 quantile.

Come trovare la mediana nelle statistiche

Il metodo per calcolare questo valore dipende in gran parte dal tipo di serie di variazioni che abbiamo: discrete o intervallate. Nel primo caso la mediana si trova semplicemente nelle statistiche. Tutto quello che devi fare è trovare la somma delle frequenze, dividerla per 2 e poi aggiungere ½ al risultato. Sarebbe meglio spiegare il principio di calcolo utilizzando il seguente esempio. Diciamo che abbiamo raggruppato i dati sulla fertilità e vogliamo scoprire qual è la mediana.

Numero del gruppo familiare per numero di figli	Numero di famiglie

Dopo alcuni semplici calcoli, troviamo che l'indicatore richiesto è: 195/2 + ½ = opzione. Per scoprire cosa significa, dovresti accumulare in sequenza le frequenze, iniziando con le opzioni più piccole. Quindi, la somma delle prime due righe ci dà 30. È chiaro che qui non ci sono 98 opzioni. Ma se al risultato aggiungiamo la frequenza della terza opzione (70), otteniamo una somma pari a 100. Contiene esattamente la 98a opzione, il che significa che la mediana sarà una famiglia con due figli.

Per quanto riguarda le serie di intervalli, solitamente viene utilizzata la seguente formula:

M e = X Me + i Me * (∑f/2 - S Me-1)/f Me, in cui:

• X Me - il primo valore dell'intervallo mediano;
• ∑f - numero di serie (somma delle sue frequenze);
• i Ме - il valore dell'intervallo mediano;
• f Me - frequenza dell'intervallo mediano;
• S Ме-1 è la somma delle frequenze cumulative negli intervalli che precedono la mediana.

Ancora una volta, è abbastanza difficile da capire senza un esempio. Supponiamo che ci siano dati sul valore

Stipendio, mille rubli.		Frequenze accumulate

Per utilizzare la formula sopra, dobbiamo prima determinare l'intervallo mediano. Come intervallo, scegliere quello la cui frequenza accumulata supera la metà della somma totale delle frequenze o è uguale ad essa. Quindi, dividendo 510 per 2, troviamo che questo criterio corrisponde all'intervallo con un valore salariale di 250.000 rubli. fino a 300.000 rubli. Ora puoi sostituire tutti i dati nella formula:

M e = X Me + i Me * (∑f/2 - S Me-1)/f Me = 250 + 50 * (510/2 - 170) / 115 = 286,96 mila rubli.

Ci auguriamo che il nostro articolo ti sia stato utile e che ora tu abbia una chiara comprensione di cosa sia una mediana nelle statistiche e di come dovrebbe essere calcolata.

Un numero che caratterizza un campione (ad esempio, un insieme di numeri). Se tutti gli elementi del campione sono diversi, la mediana è il numero del campione tale che esattamente la metà degli elementi del campione sono maggiori di esso e l'altra metà è inferiore. Più in generale, la mediana può essere trovata ordinando gli elementi di un campione in ordine crescente o decrescente e prendendo l'elemento centrale. Ad esempio, il campione (11, 9, 3, 5, 5) dopo l'ordinamento diventa (3, 5, 5, 9, 11) e la sua mediana è il numero 5. Se il campione ha un numero pari di elementi, il la mediana potrebbe non essere determinata in modo univoco: per i dati numerici, viene spesso utilizzata la semisomma di due valori adiacenti (ovvero, la mediana dell'insieme (1, 3, 5, 7) è considerata uguale a 4), per maggiori dettagli vedere.

La mediana può essere definita anche per variabili casuali: in questo caso divide la distribuzione a metà. In parole povere, la mediana di una variabile casuale è un numero tale che la probabilità di ottenere il valore della variabile casuale alla sua destra è uguale alla probabilità di ottenere il valore alla sua sinistra (e sono entrambi uguali a 1/2); Per una definizione più precisa, cfr.

Si può anche dire che la mediana sia il 50° percentile, lo 0,5 quantile o il secondo quartile di un campione o di una distribuzione.

Proprietà della mediana per variabili aleatorie

F(x) = 0,5 (\displaystyle F(x)=0,5)

Se la distribuzione è una funzione continua e strettamente crescente, la soluzione dell'equazione è unica. Se la distribuzione presenta discontinuità, la mediana può coincidere con il valore minimo o massimo (estremo) possibile della variabile casuale, il che contraddice la comprensione “geometrica” di questo termine.

La mediana è una caratteristica importante della distribuzione di una variabile casuale e, come il valore atteso, può essere utilizzata per centrare la distribuzione. Poiché le stime della mediana sono più robuste, la sua stima potrebbe essere preferibile per le distribuzioni con la cosiddetta. code pesanti. Tuttavia, i vantaggi della stima della mediana rispetto all’aspettativa matematica possono essere discussi solo se queste caratteristiche della distribuzione coincidono, in particolare, per le funzioni di densità di probabilità simmetriche.

La mediana è determinata per tutte le distribuzioni e, in caso di ambiguità, viene naturalmente definita ulteriormente, mentre l'aspettativa matematica può non essere determinata (ad esempio per la distribuzione di Cauchy).

Esempio di utilizzo

Supponiamo che ci siano 19 poveri e un milionario in una stanza. Ogni persona povera ha 5 dollari e ogni milionario ha 1 milione di dollari (10 6). Il totale è $ 1.000.095.Se dividiamo equamente il denaro tra 20 persone, otteniamo $ 50.004,75. Questa sarà la media aritmetica della quantità di denaro posseduta da tutte le 20 persone presenti nella stanza.

La mediana in questo caso sarà pari a $5 (metà della somma del decimo e dell'undicesimo, mediano valori della serie classificata). Questo può essere interpretato come segue. Avendo diviso la nostra azienda in due gruppi uguali di 10 persone, possiamo dire che nel primo gruppo ognuno non ha più di 5 dollari e nel secondo non meno di 5 dollari. In generale possiamo dire che la mediana è quanto la persona “media” ha portato con sé. Al contrario, la media aritmetica è una caratteristica inappropriata, poiché supera notevolmente la quantità di denaro a disposizione della persona media.