ماجستير. التكاملات السطحية من النوع الثاني
الحد الأدنى النظرييواصل هذا الموضوع مناقشة التكاملات المنحنية والسطحية التي بدأت في الموضوع "". يوصى بالتعرف على هذا الموضوع مسبقًا. بسبب التعقيد الأكبر للموضوع، التكاملات المنحنية والسطحية
أما النوع الثاني فيتم تناوله بشكل منفصل. تتم هنا مناقشة التكاملات السطحية من النوع الثاني، والتي ربما تكون أكثر العمليات التكاملية تعقيدًا
تحليل وظائف العديد من المتغيرات. ستكون الخطة مشابهة تمامًا للنظر في التكامل المنحني من النوع الثاني. لنبدأ بالتطبيقات المادية،
وبعد ذلك سوف ننتقل إلى الجانب الرياضي الرسمي.1. التطبيقات الفيزيائية للتكامل السطحي من النوع الثاني
الطريقة الأكثر طبيعية لإدخال التكامل السطحي من النوع الثاني هي النظر في تدفق السائل عبر سطح ما. لنبدأ بحالة بسيطة:
يتدفق السائل على طول المحور السيني بسرعة ثابتة. دعونا نختار منطقة متعامدة مع التدفق ونجد كتلة السائل الذي يمر عبرها
لها في الوقت المناسب. خلال هذا الوقت، تم إنشاء "متوازي الأضلاع" بارتفاع ومساحة قاعدية تبلغ . كتلة هذا "متوازي الأضلاع"
يساوي، أين هي كثافة السائل.
الآن دع السائل يتدفق بالتوازي مع المستوى بزاوية مع المحور السيني، ولكن بسرعة. الموقع من السابق
في حالة أننا سنظل نضعه بشكل عمودي على محور الإحداثي السيني. مع مرور الوقت، يمر عبره "متوازي الأضلاع" المائل (انظر الشكل 1). كتلتها
يساوي . لاحظ أن إدخال وحدة متجهة عادية إلى الموقع يسمح لنا بالكتابة.
يتم تقديم متجه رسمي لمنطقة أولية، معامله يساوي، ويتزامن اتجاهه مع اتجاه المتجه
عادي للموقع. ثم. يتيح لك هذا الترميز عدم القلق بشأن اتجاه ناقل سرعة المائع فيما يتعلق
إلى الموقع.ويبقى التخلي عن صغر المساحة التي يتدفق من خلالها السائل، وافتراض وجود معامل واتجاه ثابت للسرعة. ثم
وينقسم السطح إلى أجزاء صغيرة، حيث يمكن اعتبار ناقل السرعة ثابتًا. كتلة السائل الذي يمر عبر السطح
ويعطى تقريبا من المبلغ.
سيتم الحصول على الصيغة الدقيقة في حدود تقسيم السطح إلى أجزاء متناهية الصغر. النهاية هي تكامل سطحي من النوع الثاني:.
تم عند كتابة هذا القسم استخدام جزء من مادة تعليمية من مدرس قسم الفيزياء العامة يستخدمها في فصول الندوات.2. تعريف التكامل السطحي من النوع الثاني
الآن عن البناء الرسمي للتكامل. نظرا لحقيقة أن مجال المتجه متكامل على السطح، فمن المنطقي توضيح الجانب الذي
السطح، يتم حساب التكامل (كما هو الحال عند حساب تدفق السائل: يتدفق السائل إلى السطح أو يتدفق منه). لذلك، تم تحديده بشكل خاص
أن السطح الذي يتم تنفيذ التكامل عليه يجب أن يكون ذو وجهين أو قابلاً للتوجيه (أي أن شريط موبيوس ككل لن يعمل). سطح
موجهة على الفور، أي. يتم تحديد اتجاه معين للخط العمودي على السطح (على سبيل المثال، إذا تم حساب التكامل على كرة، فيمكن تحديد العمودي
موجهة من المجال أو في المجال). مكونات الحقل هي، في الحالة العامة، وظائف نقطة. سطح التكامل
يتم تقسيمها إلى أجزاء صغيرة، ويتم تحديد نقطة في كل جزء ويتم تجميع المبلغ
,
أين هي مساحة إسقاط العنصر على المستوى، هي مساحة إسقاط هذا العنصر على المستوى، هي المساحة
إسقاط هذا العنصر على المستوى. نقوم بجمع جميع العناصر التي ينقسم إليها السطح:
وانتقل إلى الحد الأقصى، وتوجيه قطر أكبر منطقة جزئية إلى الصفر. النهاية هي تكامل سطحي من النوع الثاني
.
دعونا نوضح كيفية تقليل هذا التكامل للنموذج من الخطوة 1. للقيام بذلك، سيتعين عليك إجراء انحرافات صغيرة ذات طبيعة هندسية بحتة. فليكن هناك
مستوى يتقاطع مع محاور الإحداثيات (انظر الشكل 2). الجزء من هذا المستوى الواقع في الثُمن الأول تبلغ مساحته . تحتاج إلى العثور على المنطقة
جميع الإسقاطات المتعامدة الثلاثة لجزء معين من المستوى على مستويات الإحداثيات. وكما هو معروف فإن مساحة إسقاط الشكل تساوي حاصل ضرب المساحة
الشكل نفسه وجيب تمام الزاوية بين مستوى الشكل والمستوى الذي يتم إسقاطه عليه (انظر الشكل 3). أولئك. بحاجة إلى العثور على الزوايا التي تجعل
مستوى مع طائرات الإحداثيات. الزاوية بين مستويين تساوي الزاوية بين عموديهما. الوحدة العادية للطائرة لديها مكونات،
والتي هي جيب تمام الاتجاه. ولذلك فإن الزاوية بين المستوى والمستوى متساوية (انظر الشكل 2)، وبالتالي .
نفس العلاقة ستكون صالحة للمناطق متناهية الصغر: . وبالمثل.
وبأخذ هذه العلاقات في الاعتبار، يأخذ التكامل الشكل
.
بالمناسبة، هذا النوع من التسجيل أكثر وضوحا، لذلك سنعمل معه.يؤدي عكس الاتجاه الطبيعي إلى تغيير إشارة التكامل.
3. حساب التكامل السطحي من النوع الثاني
بعد اختزال التكامل إلى نموذج يحتوي على اتجاه جيب تمام العمودي إلى السطح، يتم تقليل المشكلة بشكل أساسي إلى كتابة الوحدة العادية
مع مزيد من الحساب للتكامل السطحي من النوع الأول. هناك بعض التفاصيل في هذه الإجراءات، لذلك دعونا نلقي نظرة على الحساب بالتفصيل
تكاملات من هذا النوع.لنبدأ بالحالة التي يتم فيها إعطاء سطح التكامل بمعادلة صريحة، على سبيل المثال،
. ثم يتم كتابة المتجه العادي على النحو التالي:
,
وعنصر مساحة السطح.
ونتيجة لذلك، يأخذ التكامل السطحي الشكل التالي:
, (1)
أين هي منطقة المستوى الذي يتم إسقاط سطح التكامل عليه.من الممكن أن يكون سطح التكامل قد تم إسقاطه بشكل صحيح على المستوى (والمعطى بواسطة المعادلة) أو على المستوى
(وتعطى بالمعادلة). ثم يتم تعديل الصيغة التي يتم من خلالها حساب التكامل بشكل طفيف:
(2)
أو
. (3)
بالطبع، لا ينصح بحفظ مثل هذه الصيغ: من السهل الخلط بين شيء ما - فمن الأفضل استعادتها فيما يتعلق بصيغة معينة
الحساب مرة أخرى، بناءً على صيغة المتجه العادي ومساحة عنصر سطحي صغير.هناك حالة واحدة مميزة عندما يتم إسقاط السطح بشكل صحيح على جميع مستويات الإحداثيات الثلاثة، أي. من المعادلة السطحية أي متغير
يمكن التعبير عنها بشكل لا لبس فيه. ثم يتم تبسيط الحساب بشكل كبير. انتبه إلى بنية الصيغ (1) - (3). في كل واحد منهم ثلاثة
المصطلحات، وواحد منهم يبدو أبسط من الآخرين. عند إسقاط سطح على مستوى، فإن هذا المصطلح يحتوي على المكون
مجالات ؛ عند إسقاطه على مستوى، هذا هو المصطلح الذي يحتوي على المكون؛ عندما يتم عرضه على متن طائرة، هذا هو المصطلح
تحتوي على مكون. إذا كان السطح يبرز بشكل صحيح على أي مستوى إحداثي، فسنقوم بتقسيم التكامل
إلى ثلاثة أجزاء وتصميم كل جزء بالطريقة الأكثر ملاءمة:
.وأخيرا، حالة تحديد السطح حدوديا
.
كما هو الحال عند حساب التكامل السطحي من النوع الأول، يجب أخذ ثلاثة يعقوبيين بعين الاعتبار:
.
يتم التعبير عن اتجاه جيب التمام للوضع الطبيعي من خلالهم:
,
عنصر السطح
.
وهكذا نحصل على التكامل
,
أين هو نطاق تغييرات المعلمات المقابلة لسطح التكامل.4. صيغة ستوكس. صيغة أوستروجرادسكي غاوس
يرتبط التكامل السطحي من النوع الثاني بصيغتين تجدان تطبيقات مختلفة، بما في ذلك التطبيقات الفيزيائية.
صيغة ستوكس:
,
أين ،
يتم تمديد السطح فوق الكفاف، ويتوافق اجتياز الكفاف مع اختيار الوضع الطبيعي للسطح وفقًا لقاعدة المسمار الأيمن.
التوضيحات مطلوبة إذا كان سطح التكامل به "ثقوب".
صيغة جرين هي حالة خاصة من هذه الصيغة. بالإضافة إلى ذلك، من صيغة ستوكس يتبع شرط استقلال التكامل المنحني للثانية
نوع من شكل المسار.صيغة أوستروجرادسكي غاوس.
لحقل ناقلاتتم استيفاء الصيغة
حيث يحد السطح من الحجم.صيغة Ostrogradsky-Gauss لها تطبيقات مختلفة. دعونا ننظر إلى اثنين منهم. أولاً، من السهل إثبات إمكانية حساب حجم الجسم
وفقا للصيغةثانيًا، في بعض الأحيان يكون من الضروري حساب تكامل سطحي من النوع الثاني على سطح مفتوح، الأمر الذي يتطلب حسابات مرهقة.
ثم يتم إغلاق السطح، ويتم تحويل التكامل إلى تكامل ثلاثي، ويتم طرح التكامل الموجود على السطح المضاف (انظر المثال أدناه).ملحوظة. تتم كتابة صيغ Stokes وOstrogradsky-Gauss بسهولة أكبر في تحليل المتجهات باستخدام التفاف وتباعد مجال المتجهات.
أمثلة على حساب التكاملات السطحية من النوع الثاني
مثال 1. تكامل الطائرة.. ثم نحصل على) أجزاء من القطع المكافئ الإهليلجي (طبيعي خارجي).
دعونا نعيد كتابة التكامل في النموذج
.
يتم إسقاط سطح التكامل - القطع المكافئ الإهليلجي - بشكل صحيح فقط على المستوى، لذلك نكتب معادلة السطح في الصورة
.
أوجد وحدة المتجه العادي:.
يمكن تعميم مفهوم التكامل المزدوج على منطقة مسطحة بسهولة على حالة التكامل على السطح. لتكن (S) سطحًا (مغلقًا أو مفتوحًا) ودالة متصلة لنقطة على هذا السطح. قسّم (S) إلى أجزاء
ودع مساحات هذه الأجزاء وأي نقاط تقع على هذه الأجزاء. تجميع مجموع المنتجات
ويطلق على نهاية هذا المجموع مع الزيادة اللانهائية في عدد الأقسام والنقصان اللانهائي في كل جزء تكامل الدالة على السطح
لنفترض أن الخطوط المستقيمة الموازية للمحور Z تتقاطع مع السطح عند نقطة واحدة فقط (الشكل 48) ودع الإسقاط (S) يكون على مستوى XOY. باستخدام الصيغة (26) التي تحدد العلاقة بين مساحة السطح الأولية (S) والمساحة المقابلة لإسقاطها، يمكننا تقليل التكامل على السطح (S) إلى التكامل على المساحة المسطحة:
في هذه الحالة يفترض أنها تختلف عن الصفر وأن قيمة الدالة عند النقطة N من المنطقة تتطابق مع قيمة الدالة المحددة على السطح عند تلك النقطة M والتي يتطابق إسقاطها مع . إذا كانت معادلة السطح (S) معطاة بالصورة الصريحة (22) وتم التعبير عن الدالة بدلالة الإحداثيات، فعند التكامل عليها يكفي استبدال الدالة في التعبير. يتم تحديد المقام الموجود على الجانب الأيمن من (29) بثلث الصيغ (24).
لاحظ أنه من الواضح أن التكاملات السطحية تحتوي على جميع خصائص التكامل المزدوج المشار إليها في، على وجه الخصوص، نظرية القيمة المتوسطة التي تنطبق عليها.
دعونا الآن نثبت إحدى الصيغ الرئيسية في نظرية التكاملات المتعددة - صيغة أوستروجرادسكي، التي تنشئ اتصالاً بين التكامل الثلاثي على الحجم والتكامل على السطح (S) الذي يحد هذا الحجم. سننظر في كيفية وأين تتقاطع الخطوط المستقيمة الموازية للمحور Z (S) في ما لا يزيد عن اثنين
نقاط. دعونا نحتفظ بنفس التدوين كما في الشكل. 40. ولندخل في الاعتبار أيضًا اتجاه العمودي إلى (S)، وسنفترض أنه موجه خارج الحجم (V) (الطبيعي الخارجي) (الشكل 50). يشكل هذا الاتجاه زاوية حادة مع محور OZ في الجزء العلوي من السطح (I)، وزاوية منفرجة في الجزء السفلي (I). ولذلك، في الجزء السفلي، نلاحظ أنه على خط اتصال السطح (5) مع الاسطوانة البارزة (الشكل 50). الصيغة (26) تعطي
لنكن مع المشتقة مستمرين في المنطقة حتى (S). دعونا نفكر في التكامل الثلاثي للدالة، وباستخدام الصيغة (١٦)، سيكون لدينا
لكن تكامل المشتق يساوي الفرق بين قيم دالة المشتق العكسي عند الحدين العلوي والسفلي:
بالاستبدال وفقًا للصيغة (30)، نختصر التكامل إلى التكامل على (S)، وفي التكامل الأول، الذي يحتوي على الإحداثيات المتغيرة للجزء (I) من السطح (S)، سيتعين علينا استخدام أول الصيغ (30)، وحصلنا على التكامل على (II)، في التكامل الثاني الذي يحتوي على سيتعين عليك استخدام الصيغة الثانية (30)، وتحصل على التكامل على (I):
لم يعد من الممكن كتابة رموز z، حيث يتم الإشارة إليها على أي جزء من السطح يتم تنفيذ التكامل. على الجانب الأيمن مجموع التكاملات على الجزأين (II) و (I)، أي التكامل على الكل
الأسطح (س):
إذا كانت الوظائف التي لها خصائص الدالة R، مع مراعاة ذلك
وبناء على (31) يمكننا كتابة صيغة التكامل بالأجزاء:
وبنفس الطريقة تمامًا، يمكننا إثبات دالتين أخريين
وبجمع الصيغ الثلاث التي تم الحصول عليها مصطلحًا بعد مصطلح، نصل إلى صيغة أوستروجرادسكي
على غرار (31،) تتم كتابة صيغ التكامل بالأجزاء للمشتقات المتعلقة بـ x و y.
من أجل الإيجاز، لا نكتب هنا الوسائط x، y، z للوظائف P، Q، ولكن يجب أن نتذكر أن هذه وظائف محددة في الحجم ومستمرة مع مشتقاتها.
في الفصل التالي سنقدم عددًا كبيرًا من الأمثلة على تطبيق صيغة أوستروجرادسكي.
الكميات هي وظائف محددة على السطح (S). لقد اعتبرناها مستمرة. يمكن للمرء أن يضع افتراضًا أكثر عمومية، أي افتراض أن (S) مقسمة إلى عدد محدود من القطع، تكون الوظائف المشار إليها متصلة في كل منها. سيكون هذا هو الحال، على سبيل المثال، إذا كان (S) متعدد السطوح.
عند استخلاص الصيغة (31) افترضنا أن الخطوط المستقيمة الموازية للمحور تتقاطع مع سطح (S) المنطقة بما لا يزيد عن نقطتين. ليس من الصعب تعميم هذه الصيغة على مجالات ذات شكل أكثر عمومية. نلاحظ أولا أنه إذا كان السطح (S)، بالإضافة إلى الجزء العلوي (II) والجزء السفلي (I)، لديه جزء جانبي أسطواني مع مولدات موازية للمحور، ثم على هذا الجزء الجانبي وإضافة هذا الجزء الموجود على الجانب الأيمن من الصيغة (31) لا يغير قيمة التكامل السطحي، لذلك يبقى برهان الصيغة كاملا صالحا. وفي حالة أكثر عمومية يكفي استخدام الأسطح الأسطوانية ذات المولدات الموازية للمحور لتقسيمها إلى عدد محدود من الأجزاء التي تحقق الشروط السابقة، وتطبيق الصيغة (31) على كل جزء. بإضافة الصيغ التي تم الحصول عليها بهذه الطريقة، سيكون لدينا على الجانب الأيسر تكامل ثلاثي على كامل الحجم. على الجانب الأيمن سيكون لدينا مجموع التكاملات على جميع أسطح تلك الأجزاء التي قسمنا إليها (v). التكاملات الموجودة على الأسطح الأسطوانية المساعدة المخفضة، كما هو موضح أعلاه، تساوي الصفر. وبالتالي، نتيجة للجمع على الجانب الأيمن، سيكون لدينا تكامل على السطح (S) للحجم الأصلي. لذلك، تبين أن الصيغة (31) صالحة للمجالات ذات الشكل الأكثر عمومية.
دعونا ننظر إلى تكاملات الدوال المحددة على الأسطح، أو ما يسمى بالتكاملات السطحية، فنظرية التكاملات السطحية تشبه في كثير من النواحي نظرية التكاملات المنحنية. هناك تكاملات سطحية للأول و
من النوع الثاني.
4.1. التكاملات السطحية من النوع الأول. دع الدالة f(x, y, z)
محددة على سطح أملس متعدد القطع S، ويحدها محيط أملس متعدد القطع (الشكل 4.1). دعونا كسرها
على التوالي ∆ ق 1، ∆ ق 2 ...، ∆ ق ن. بأخذ نقطة عشوائية M i (x i, y i, z i) داخل كل جزء S i, i = 1, n، نحسب قيمة الدالة فيه ونجمع المبلغ التالي:
σ n= ∑ f (x i, y i, z i) ∆ s i | |||||
ط= 1 | للدالة f (x, y, z) بواسطة |
||||
وهو ما يسمى متكاملة | |||||
السطح س. | |||||
الحد النهائي الأول من هذا | بينما يسعى | ||||
أكبر π لأقطار جميع الأسطح الجزئية S i | |||||
1، ن |
|||||
إذا كان موجودا ولا يعتمد على طريقة تقسيم السطح إلى أجزاء جزئية ولا على اختيار النقاط فيسمى التكامل السطحي من النوع الأول (على مساحة السطح)من الوظيفة
f (x, y, z) على طول السطح S ويشار إليه بالرمز | ∫∫ f(x, y, z) ds. |
|
لذلك، بحكم التعريف | ||
= ∫∫ f(x, y, z) ds. | ||
I = lim ∑ f(xi , yi , zi ) ∆ si | ||
φ → 0i = 1 | ||
التكامل السطحي من النوع الأول هو تعميم للتكامل المزدوج، وبالتالي فإن شروط وجود التكامل المزدوج وخصائصه تنتقل بسهولة إلى التكامل السطحي من النوع الأول.
حساب التكاملات السطحية من النوع الأول يتم الاختزال لحساب التكاملات المزدوجة: بناءً على المعادلة السطحيةس،
يتم تحويل التكامل إلى متغيرين، سيكون نطاقهما هو إسقاط السطح S على المستوى الإحداثي المقابل لهذه المتغيرات.
دع السطح S يتم تعريفه بالمعادلة z = z (x, y) و z (x, y) تكون مستمرة مع مشتقاتها الجزئية z ′ x, z ′ y في مجال مغلق S xy، وهو إسقاط السطح S على المستوى الإحداثي xOy، إذن
∫∫ f(x, y, z) ds= ∫∫ f(x, y, z(x, y)) 1 + (z′ x ) 2 + (z′ y ) dxdy. | ||
س س ص | ||
تعبر هذه الصيغة عن التكامل السطحي للنوع الأول من خلال التكامل المزدوج على إسقاط السطح S على المستوى الإحداثي xOy.
يتم حساب التكاملات السطحية من النوع الأول على السطح S بطريقة مماثلة من خلال التكاملات المزدوجة على إسقاطاته
تنسيق الطائرات xOz وyOz على التوالي: | |||
∫∫ f (x ,y ,z )ds = ∫∫ f (x ,y (x ,z ),z ) | 1+ (y ′ x )2 + (y ′ z )dxdz , | ||
س س ز | |||
∫∫ f (x, y,z)ds= ∫∫ f (x(y,z), y,z) | 1 + (x′ y)2 + (x′ z)dydz. | ||
Syz | |||
باستخدام التكاملات السطحية من النوع الأول، يمكن حساب مساحة السطح وكذلك الكتلة والعزوم الساكنة وعزوم القصور الذاتي وإحداثيات مركز الكتلة لأسطح المواد ذات كثافة توزيع الكتلة السطحية المعروفة.
مثال 4.1. احسب
∫∫ 1 + 4 x 2 + 4 y 2 ds , حيث S جزء من القطع المكافئ
مواضع الدوران z = 1 − x 2 − y 2 , مقطوعة بالمستوى z = 0 .
حل. دعونا نصمم السطح
S إلى الطائرة xOy .
الإسقاط S xy عبارة عن دائرة تحدها الدائرة x 2 + y 2 = 1 (الشكل 1).
4.2). سنحسب التكامل السطحي المعطى باستخدام الصيغة (4.2)، والتي نجد لها z ′ x = − 2 x , z ′ y = − 2 y . ثم ارتكاب مزدوج
أساسي | إلى القطبي | الإحداثيات, | Sxy عبارة عن دائرة، |
||||||||
1 +4 x 2 +4 y 2 ds =∫∫ | 1+ 4x 2 + 4ص 2 | 1 + 4x2 + 4y2 dxdy= |
|||||||||
س س ص | |||||||||||
= ∫∫ (1 +4 x 2 +4 y 2 ) dxdy = | |||||||||||
س س ص | |||||||||||
= ∫ د ϕ ∫ (1 +4 ρ 2 ) ρ د ρ =∫ | + ρ 4) | د ϕ= | ∫ د ϕ . |
||||||||
4.2. الأسطح ذات الوجهين. يسمى السطح S
ذو وجهين، إذا كان العبور على طول أي كفاف مغلق ملقى على السطح S ولا يتقاطع مع حدوده، عند العودة إلى نقطة البداية، لا يغير اتجاه العمودي إلى السطح. خلاف ذلك، يسمى السطح من جانب واحد. أمثلة على الأسطح ذات الوجهين: المستوي والكرة وأي سطح محدد بالمعادلة z = z (x, y)، حيث z = z (x, y)، z ′ x (x, y)، z ′ y (x) ، ذ) - مستمر في بعض المناطقز. مثال على السطح أحادي الجانب هو شريط موبيوس.
4.3. التكامل السطحي من النوع الثاني. دعونا - سطح أملس تعطى بالمعادلةض = ض (س، ص) والدالة و (س، ص، ض)
محددة عند نقاط السطح S.
دعونا نختار أحد جوانب السطح، أي أحد الاتجاهين المحتملين للخط العمودي عند نقاط السطح (هذه هي الطريقة التي قمنا بها بتوجيه السطح). إذا كانت الأعراف تشكل زوايا حادة مع
محور أوز ، ثم سنتحدث عنهالجانب العلوي من السطح (حول الاتجاه الإيجابي للطبيعي ) ، وإذا كانت الأعراف -زوايا منفرجة مع محور أوز، فنحن نتحدث عن الجانب السفلي من السطح (الاتجاه السلبي للعمودي).
دعونا نقسم السطح S بشكل تعسفي إلى أجزاء n S 1، S 2 ...، S n، ومن خلال (S xy ) i نشير إلى إسقاط الجزء i من السطح
إلى الطائرة xOy. ضمن كل سطح جزئي S i , i = 1, n، اختر نقطة عشوائية M i (x i , y i , z i ) واحسب قيمة الدالة
في ذلك سوف نجعل المبلغ
σ n= ∑ f (x i, y i, z i) ∆ s i, i = 1
حيث ∆ s i - المساحة (S xy) i، مأخوذة بعلامة زائد إذا تم تحديد الجانب العلوي من السطح S وبعلامة ناقص إذا تم تحديد الجانب السفلي
السطح س. يسمى هذا المبلغ n مجموع لا يتجزأللدالة f(x,y,z).
الحد النهائي I للمجموع التكاملي، حيث أن أكبر lect لجميع أقطار الإسقاط (S xy ) i يميل إلى الصفر، إذا كان موجودًا و
لا يعتمد على طريقة تقسيم السطح S ولا على اختيار النقاط
M i (x i، y i، z i)، ثم يسمى هذا الحد التكامل السطحي للنوع الثاني من الوظائفو(س، ص، ض) على طول الجانب المحدد من السطح بواسطة المتغيرات x و y ويشار إليهما بـ ∫∫ f (x, y, z) dxdy. وهكذا، بحسب
تعريف
السطح S في المتغيرات x و y.
وبالمثل، يمكنك تحديد التكاملات السطحية من النوع الثاني على جانب محدد من السطح S في المتغيرين y وz، في المتغيرين x وz:
∫∫ f(x, y, z) dydz, | ∫∫ f(x, y, z) dxdz. |
دع P (x، y، z)، Q (x، y، z)، R (x، y، z) تكون دوال قابلة للتكامل
السطح S في المتغيرات y وz وx وz وx وy على التوالي. مجموع التكاملات
∫∫ P(x, y, z) dydz, | ∫∫ س(س، ص، ض) دكسدز، | ∫∫ R(x, y, z) dxdy | |
ويسمى التكامل العام من النوع الثاني ويشار إليه | |||
∫∫ P(x, y, z) dydz+ Q(x, y, z) dxdz+ R(x, y, z) dxdy. | |||
وبما أننا نعتبر السطح S ذو وجهين والتكامل يمتد إلى جانب معين منه، إذن عندما يتغير جانب سطح التكامل يتغير تكامل سطح النوع الثاني إلى العكس– وهذا هو اختلافه عن التكامل السطحي للنوع الأول.
حساب التكاملات السطحية من النوع الثاني يقلل من حساب التكاملات المزدوجة.
دع السطح الأملس الموجه (اختر الجانب العلوي) S يُعطى بالمعادلة z = z (x، y)، حيث z (x، y) مستمر في
منطقة مغلقة S xy - إسقاط السطح S على المستوى xOy؛ الدالة f(x, y, z) مستمرة على S. ثم الصيغة صالحة
∫∫ f(x, y, z) dxdy= ∫∫ f(x, y, z(x, y)) dxdy, | ||||
س س ص | ||||
معبرا عن التكامل السطحي للنوع الثاني على المتغيرات x و | ||||
من خلال مزدوج. إذا اخترنا الجانب السفلي من السطح S، ثم في الأمام |
||||
لا يتجزأ، ستظهر علامة الطرح على الجانب الأيمن. | ||||
الصيغ صالحة بالمثل | ||||
∫∫ f(x, y, z) dydz= ∫∫ f(x(y, z), y, z) dydz, | ||||
Syz | ||||
∫∫ f(x, y, z) dxdz= ∫∫ f(x, y(x, z), z) dxdz, | ||||
س س ز | ||||
حيث السطح S | وفقا للمعادلات | س = س (ص، ض) | ||
y = y(x, z) وSyz | و س سز - | توقعات السطح S، على التوالي | ||
الطائرات yOz وxOz.
لحساب التكامل العام (4.6)، يتم استخدام الصيغ (4.7) – (4.9) إذا تم إسقاط السطح S بشكل فريد على الكل
تنسيق الطائرات. في الحالات الأكثر تعقيدًا، يتم تقسيم السطح S إلى أجزاء لها الخصائص المشار إليها، ويتم تقديم التكامل العام في شكل تكاملات فوق هذه الأجزاء.
مثال 4.2.احسب
∫∫ (y 2 + z 2 ) dxdy ، حيث S هو الجانب العلوي
السطح ض = | 1 - س 2 | قطع مسطحة |
||||||||
النرد ص = 0، ص = 1. | ||||||||||
حل. المعادلة س 2 + ض 2 = 1 - |
||||||||||
يتم تحديد اسطوانة دائرية مع المولدات، |
||||||||||
بالتوازي مع محور Oy، والمستوى y = 0 و |
||||||||||
ص = 1 | موازي | تنسيق |
||||||||
طائرة xOz (الشكل 1). | تنبؤ |
|||||||||
السطح S على المستوى xOy هو |
||||||||||
المستطيل S xy المحدد بالمتباينات − 1 ≥ x ≥ 1, | 0 ≥ ص ≥ 1. |
|||||||||
ثم بالصيغة (4.7) لدينا | ||||||||||
∫∫ (y2 + z2 ) dxdy= ∫∫ (y2 + (1 − x2 )) dxdy= ∫ dx∫ (y2 − x2 + 1) dy= |
||||||||||
س س ص | −1 | |||||||||
+ (1− × 2 )ص ) | ||||||||||
= ∫ دس ( | ||||||||||
−1 | ||||||||||
- x2 ) دكس | ||||||||||||||||||||||||||||||
= ∫ ( | ||||||||||||||||||||||||||||||
−1 | −1 | |||||||||||||||||||||||||||||
مثال 4.3. احسب | ||||||||||||||||||||||||||||||
∫∫ xdydz+ ydxdz+ zdxdy، حيث S هو الجزء العلوي | ||||||||||||||||||||||||||||||
جانب جزء من المستوى x + z − 1 = 0 | ||||||||||||||||||||||||||||||
مقطوعة بالطائرات y = 0، y = 4 و | ||||||||||||||||||||||||||||||
تقع في الثماني الأول (الشكل 4.4). | ||||||||||||||||||||||||||||||
حل. إسقاط السطح S على | ||||||||||||||||||||||||||||||
المستوى xOy هو المستطيل S xy، | ||||||||||||||||||||||||||||||
محددة من قبل عدم المساواة 0 ≥ س ≥ 1، | ||||||||||||||||||||||||||||||
0 ≥ ص ≥ 4 . إسقاط السطح S على | ||||||||||||||||||||||||||||||
مستوى yOz مستطيل | S yz، التي تحددها عدم المساواة |
|||||||||||||||||||||||||||||
0 ≥ ض ≥ 1,0 ≥ ص ≥ 4. بما أن المستوى S عمودي على المستوى |
||||||||||||||||||||||||||||||
xOz ، ثم∫∫ ydxdz = 0. ثم، بالصيغتين (4.7) و (4.9) لدينا |
||||||||||||||||||||||||||||||
∫∫ xdydz+ ydxdz+ zdxdy= ∫∫ (1 − z) dydz+ |
||||||||||||||||||||||||||||||
Syz | ||||||||||||||||||||||||||||||
+ ∫∫ (1 − x) dxdy= ∫ dy∫ (1 − z) dz+ ∫ dy∫ (1 − x) dx= |
||||||||||||||||||||||||||||||
س س ص | ||||||||||||||||||||||||||||||
- ض ) | (1− س) | |||||||||||||||||||||||||||||
2 ∫ | دي = 4. |
|||||||||||||||||||||||||||||
= ∫ دي − | + ∫ دي − | |||||||||||||||||||||||||||||
4.4. صيغة أوستروجرادسكي. تنشئ صيغة أوستروجرادسكي اتصالاً بين التكامل السطحي على سطح مغلق والتكامل الثلاثي على المنطقة المكانية المحدودة بهذا السطح.
لتكن V منطقة مغلقة منتظمة يحدها السطح S، ولتكن الدوال P(x, y, z), Q(x, y, z), R(x, y, z)
تكون مستمرة مع مشتقاتها الجزئية من الدرجة الأولى في منطقة معينة. ثم تحمل الصيغة التالية:
∫∫∫( | ∂P | ∂س | ∂ R ) dxdydz= ∫∫ Pdydz+ Qdxdz+ Rdxdy, (4.10) |
|||
∂x | ∂y | ∂z | ||||
مُسَمًّىصيغة أوستروجرادسكي 1 .
باستخدام صيغة أوستروجرادسكي، من السهل حساب تكاملات الأسطح على الأسطح المغلقة.
مثال 4.4.باستخدام صيغة Ostrogradsky، احسب
∫∫ xdydz + ydxdz + com.zdxdy , | أين س | ||||||||||||||||||||||||||
جانب الهرم | محدود | طائرات | |||||||||||||||||||||||||
س + ذ + ض = 1, | س= 0,ذ= 0, | ض= 0 (الشكل 4.5). | |||||||||||||||||||||||||
وفق | |||||||||||||||||||||||||||
أوستروجرادسكي: | |||||||||||||||||||||||||||
ص(س,ذ,ض)= س,س(س,ذ,ض)= ذ,ر(س,ذ,ض)= ض. | |||||||||||||||||||||||||||
ثم: ∂ ص+ | ∂ س+ | ∂ر | = 1+ 1+ 1= 3,ونجد | ||||||||||||||||||||||||
∂س | ∂ذ | ∂ض | |||||||||||||||||||||||||
1− س | 1 −س−ذ | ||||||||||||||||||||||||||
∫∫ xdydz + ydxdz + com.zdxdy = 3 ∫∫∫ com.dxdydz = 3 ∫ dx ∫ دي | ∫ dz = | ||||||||||||||||||||||||||
1− س | 1 −س−ذ | 1− س | |||||||||||||||||||||||||
= 3 ∫ dx ∫ دي ∫ dz = 3 ∫ dx ∫ (1 − س − ذ ) دي = | |||||||||||||||||||||||||||
ذ 2 | 1− س | ||||||||||||||||||||||||||
3 ∫ dx (ذ − xy − | |||||||||||||||||||||||||||
−2 س+1 | 3 (س− 1) | ||||||||||||||||||||||||||
= 3 ∫ (1 −س−س+س2 − | ) dx = | ∫ (س − 1) 2 dx = | |||||||||||||||||||||||||
ملاحظة 4.1.إن العلاقة بين التكاملات السطحية من النوعين الأول والثاني تشبه العلاقة بين التكاملات المنحنية:
∫∫ F (س , ذ , ض ) com.dxdy = ∫∫ F (س , ذ , ض )كوسα س ,
∫∫ F (س , ذ , ض ) dydz = ∫∫ F (س , ذ , ض )كوسβ س ,
∫∫ F (س , ذ , ض ) com.dxdz = ∫∫ F (س , ذ , ض )كوسγ س ,
أين كوسα ,كوسβ ,كوسγ - اتجاه جيب التمام الطبيعي الموافق
الجانب المحدد من السطح. ,ذ) | المستمر في المنطقة سxy- الإسقاطات السطحية س |
||||||||||||||||||||||
الى الطائرة xOy;ل | - محيط شكل، | الحد | سطح | س ; ل – |
|||||||||||||||||||
إسقاط خط الفضاء لالى الطائرة | xOy , | كون |
|||||||||||||||||||||
بيت الكلب يحد من المنطقة د. دعونا نختار الجانب العلوي |
|||||||||||||||||||||||
الأسطح س. إذا كانت الوظائف ص(س, ذ, ض), س(س, ذ, ض), ر(س, ذ, ض) | مستمر |
||||||||||||||||||||||
مع مشتقاته الجزئية من الدرجة الأولى |
|||||||||||||||||||||||
الأسطح س، فإن الصيغة التالية تحمل: | |||||||||||||||||||||||
∫ بدكس + قدي + ردز = | |||||||||||||||||||||||
= ∫∫ | (∂ س | ∂ ص) com.dxdy + ( | ∂ر | ∂ س) dydz + (∂ ص | ∂ ر) com.dxdz | ||||||||||||||||||
∂س | ∂ذ | ∂ذ | ∂ض | ∂ض | ∂س | ||||||||||||||||||
(ل- يتحرك في اتجاه إيجابي) | مُسَمًّى معادلة |
||||||||||||||||||||||
إذا كان سطحيا سخذ المنطقة دعلى السطح xOy |
|||||||||||||||||||||||
(ض= 0 ) ومن (4.11) نحصل على صيغة جرين | ∂س | ∂ ص) com.dxdy . | |||||||||||||||||||||
∫ ص (س , ذ ) dx + س (س , ذ ) دي = ∫∫ ( | |||||||||||||||||||||||
∂س | ∂ذ | ||||||||||||||||||||||
وبالتالي، فإن صيغة جرين هي حالة خاصة من صيغة ستوكس. |
|||||||||||||||||||||||
لاحظ أن التكامل السطحي للنوع الثاني في الصيغة |
|||||||||||||||||||||||
يمكن استبدال ستوكس (4.11) بالتكامل السطحي للأول |
|||||||||||||||||||||||
يكتب. ثم هذه الصيغة سوف تأخذ النموذج | |||||||||||||||||||||||
∫ بدكس + قدي + ردز = | |||||||||||||||||||||||
∂س | ∂ص | ∂ر | ∂س | ∂ص | ∂ر | ||||||||||||||||||
= ∫∫ | )كوس α + ( | )كوس β + ( | )كوس γ | ||||||||||||||||||||
∂س | ∂ذ | ∂ذ | ∂ض | ∂ض | ∂س | س , | |||||||||||||||||
أينكوس α ، كوس β ، كوس γ , | يقصد | خطوط إرشاد | جيب التمام | ||||||||||||||||||||
المقابلة للجانب المحدد من السطح. | |||||||||||||||||||||||
باستخدام الصيغة | احسب |
||||||||||||||||||||||
∫ س 2 ذ 3 dx + دي + zdz , | دائرة، | تعطى بواسطة المعادلات |
|||||||||||||||||||||
س 2 + ذ 2 + 1, ض = 0 . | سطح سيخدم الجانب العلوي من نصف الكرة الأرضية |
||||||||||||||||||||||
س 2+ ذ 2+ ض 2= 1, | ض> 0 (ليسير في اتجاه إيجابي). |
||||||||||||||||||||||
في الحالات التي لا يحدث فيها التكامل على جزء من المنحنى، بل على سطح محدد. مثل التكاملات المنحنية الأضلاع، فإن التكاملات السطحية هي من النوع الأول والنوع الثاني.
التكامل السطحي من النوع الأول مكتوب في النموذج
أين F(م) = F(س، ص، ض) هي وظيفة من ثلاثة متغيرات، والسطح σ - مجال تكامل هذه الوظيفة. لو F(س، ص، ض) يساوي الوحدة، فإن تكامل السطح يساوي مساحة السطح.
تخيل زهرة عباد الشمس كبيرة إلى حد ما وبها بذور صغيرة جدًا. بعد ذلك، من مجموع أسطح البذور الصغيرة جدًا الموجودة على سطح عباد الشمس، يمكن حساب سطح عباد الشمس - قد يكون هذا تفسيرًا مبسطًا للتكامل السطحي. لماذا هذا؟
دعنا ننتقل إلى تعريف أكثر رسمية للتكامل السطحي. سطح σ مقسمة إلى نالأجزاء ذات المساحات Δ σ 1 , Δ σ 2 , ..., Δ σ ن. إذا قمت بتحديد نقطة تعسفية على كل سطح جزئي (بذرة) مأنابالإحداثيات ( ζ أنا، η أنا، ς أنا ،)، ثم يمكننا أن نلخص
يسمى هذا المجموع المجموع التكاملي للدالة F(م) على السطح σ . الآن سنقوم بتعظيم عدد هذه الأجزاء الصغيرة وقطرها الأكبر Δ σ أنا- على العكس من ذلك، تقليل. إذا كان المجموع التكاملي كأكبر أقطار الأجزاء يميل إلى الصفر (أي، كما أشرنا سابقًا، جميع الأجزاء صغيرة جدًا) له حد، فإن هذا الحد يسمى التكامل السطحي من النوع الأول من الوظيفة F(م) على السطح σ .
حساب التكامل السطحي من النوع الأول
دع السطح σ تعطى بواسطة المعادلة ض = ض(س, ذ) ، إسقاطه على الطائرة xOyهي المنطقة دxy، بينما الوظيفة ض = ض(س, ذ) ومشتقاته الجزئية مستمرة في المنطقة دxy.
مثال 1.
أين σ - جزء من الطائرة في الثماني الأول.
حل. رسم:
من معادلة المستوى نحصل على عبارة "zet": 
.
ثم المشتقات الجزئية هي: و
.
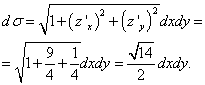سطح σ هو المثلث الموضح في الرسم اي بي سي، وإسقاطه على الطائرة xOy- مثلث AOB، والتي تقتصر على خطوط مستقيمة س = 0 , ذ= 0 و 3 س + ذ= 6. لننتقل من التكامل السطحي إلى التكامل المزدوج ونحله:
.
مفهوم التكامل السطحي من النوع الثاني
قبل الانتقال إلى تعريف التكامل السطحي من النوع الثاني، لا بد من التعرف على مفهومي جوانب السطوح والأسطح الموجهة.
دع سطح أملس يعطى في الفضاء σ . دعونا نختار نقطة تعسفية على هذا السطح مورسم المتجه العادي إلى السطح من خلاله. من خلال النقطة مسنقوم بتنفيذها أيضًا على السطح σ كفاف تعسفي ليس له نقاط مشتركة مع حدود السطح σ . نقطة مسنتحرك مع المتجه العادي على طول الكفاف بحيث يكون المتجه العمودي دائمًا متعامدًا مع السطح σ . عند عودة النقطة مإلى الموضع الأولي، هناك حالتان محتملتان: سيظل اتجاه المتجه الطبيعي كما هو أو سيتغير إلى الاتجاه المعاكس.
إذا لم يتغير اتجاه المتجه الطبيعي، فإن السطح σ تسمى الثنائية. إذا تغير اتجاه المتجه الطبيعي إلى الاتجاه المعاكس عند اجتياز الكفاف، فإن السطح يسمى أحادي الجانب. تسمى الأسطح ذات الوجهين بالأسطح الموجهة، وتسمى الأسطح ذات الجانب الواحد بالأسطح غير الموجهة.
مثال على السطح أحادي الجانب هو شريط موبيوس (في الصورة أعلاه)، والذي يمكن صنعه من شريط من الورق مع تدوير جانب واحد بمقدار 180 درجة ثم لصق الأطراف معًا. وهنا ما هو مهم هنا: بالنسبة للسطح أحادي الجانب، لم يتم تقديم مفهوم التكامل السطحي من النوع الثاني .
لذلك سننظر فقط إلى الأسطح ذات الوجهين. من أمثلة الأسطح ذات الوجهين المستويات، والمجالات، والأشكال الناقصية، والأشكال المكافئة.
يحدد الجانب الموجب للسطح ذي الوجهين اتجاه المتجه الطبيعي. ويسمى الجانب الآخر من السطح سلبيا. الجانب الإيجابي من السطح هو جانبه العلوي. إذا كانت متجهات الوحدة العادية تصنع زوايا حادة مع المحور أوز، ثم يتم تحديد الجانب العلوي من السطح ض = ض(س, ذ) ، إذا كانت الزوايا منفرجة، فالجانب السفلي من السطح.
كما في حالة التكامل السطحي من النوع الأول، يمكن تقسيم السطح إلى نالقطع. عند صياغة مفهوم التكامل السطحي من النوع الأول كان مجموع التكامل يشمل مساحات كل جزء من الأجزاء التي ضربت بها قيم الدالة F(مأنا). في حالة التكامل السطحي من النوع الثاني، لا يتم أخذ مساحات الأجزاء نفسها، ولكن مساحات إسقاطاتها على المستويات الإحداثية . ولتمييز دالة ثلاثة متغيرات عن تكامل من النوع الأول نشير إليه ر(س,ذ,ض) . ثم سيتم كتابة المجموع التكاملي على النحو التالي:
,
حيث Δ سأنا- مساحات الإسقاطات المذكورة لأجزاء من جانب السطح على المحور الإحداثي (في الوقت الحالي سنفترض ذلك على المحور xOy).
مع مثل هذه الاتفاقيات والتدوين، فإن تعريف التكامل السطحي من النوع الثاني يشبه تعريف التكامل من النوع الأول. وهي: التكامل السطحي من النوع الثاني هو نهاية مجموع متكامل معين حيث أن القطر الأكبر لأجزاء السطح المعني يميل إلى الصفر.
هو مكتوب مثل هذا:
.
في هذه الحالة الوظيفة ر(س,ذ,ض) التكامل على المتغيرات سو ذ، حيث تم إسقاط أجزاء من السطح على الطائرة xOy.
وبالمثل، يمكننا كتابة تكاملين سطحيين آخرين من النوع الثاني:
(وظيفة ص(س,ذ,ض) التكامل على المتغيرات ذو ض يوز),
(وظيفة س(س,ذ,ض) التكامل على المتغيرات ضو س، حيث يتم إسقاط أجزاء من السطح على المستوى زوكس).
مجموع هذه التكاملات
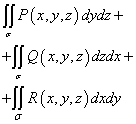
مُسَمًّى تكامل السطح العام من النوع الثاني ويتم تعيينه
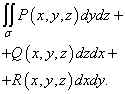
حساب التكامل السطحي من النوع الثاني
يتم حساب التكامل السطحي من النوع الثاني عن طريق تحليل التكامل السطحي العام من النوع الثاني إلى مجموع التكاملات السطحية (انظر نهاية الفقرة السابقة) واختزال كل منها إلى تكامل مزدوج.
دعونا نفكر بالتفصيل في حساب التكامل
.
دع السطح σ تعطى بواسطة المعادلة ض = ض(س, ذ) . نشير إلى الجانب الإيجابي من السطح، والجانب السلبي، والإسقاط على المستوى xOy - دxy.
وهكذا نحصل على صيغة لحساب التكامل السطحي من النوع الثاني:
إذا تم تحديد الجانب السلبي من السطح، فإن علامة التكامل تتغير:
يتم حساب التكاملين المنفصلين الآخرين - مصطلحات التكامل العام - بالمثل:
مثال 2.
,
أين σ - الجانب العلوي لجزء من المستوى مقطوع بالطائرات ذ= 0 و ذ= 4 وتقع في الثمانية الأولى.
حل. الرسم في الصورة أعلاه. بحكم التعريف، نحصل على مجموع ثلاثة تكاملات مزدوجة:
التكامل الثاني يساوي الصفر، لأن المستوى σ موازية للمحور أوي. لذلك نجد التكامل الأول والثالث:
كل ما تبقى هو جمع كل التكاملات الفردية والحصول على التكامل السطحي العام من النوع الثاني:
.
إذا كنت بحاجة إلى حساب تكامل سطحي من النوع الثاني على سطح مغلق، يمكنك الذهاب إلى تكامل ثلاثيباستخدام صيغة أوستروجرادسكي. ثم إذا كانت الوظائف ص(س، ص، ض) , س(س، ص، ض) و ر(س، ص، ض) ومشتقاتها الجزئية، هي دوال مستمرة في المجال دبليو، والذي يحده سطح مغلق σ ثم عند التكامل على السطح الخارجي يكون التساوي
مثال 3.حساب التكامل السطحي من النوع الثاني
,
أين σ - الجانب الخارجي لسطح المخروط المكون من سطح ومستوي ض = 2 .
حل. هذا السطح هو سطح مخروط ذو نصف قطر ر= 2 والارتفاع ح= 2 . هذا سطح مغلق، لذا يمكنك استخدام صيغة أوستروجرادسكي. لأن ص = 3س , س = 4ذ , ر = −ضثم المشتقات الجزئية , .
ننتقل إلى التكامل الثلاثي الذي نحله:
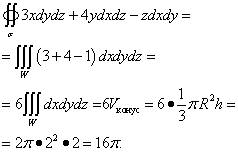
مزيد من الأمثلة على حساب التكاملات السطحية
مثال 4.حساب التكامل السطحي من النوع الأول
أين σ - السطح الجانبي للمخروط عند .
حل. منذ المشتقات الجزئية 
,
، الذي - التي
نقوم بتقليل هذا السطح المتكامل إلى سطح مزدوج:
إسقاط سطح على مستوى xOyهي دائرة مركزها نقطة الأصل ونصف القطر ر= 2، لذلك عند حساب التكامل المزدوج، ننتقل إلى نظام الإحداثيات القطبية. للقيام بذلك، دعونا نغير المتغيرات:
نحصل على التكامل التالي، والذي قمنا بحله أخيرًا:
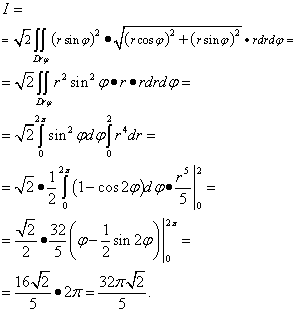
مثال 5.حساب التكامل السطحي من النوع الثاني
,
أين σ - الجزء العلوي من المثلث المتكون من تقاطع المستوى مع المستويات الإحداثية.
حل. دعونا نقسم هذا التكامل السطحي على مجموع تكاملين
، أين
.
لحساب التكامل أنا1 σ الى الطائرة يوز. الإسقاط هو مثلث او سي بي، الذي هو على متن الطائرة يوزالحد من الخطوط المستقيمة أو ذ= 0 و ض= 0 . من معادلة الطائرة مشتقة. لذلك يمكننا حساب التكامل أنا1 :
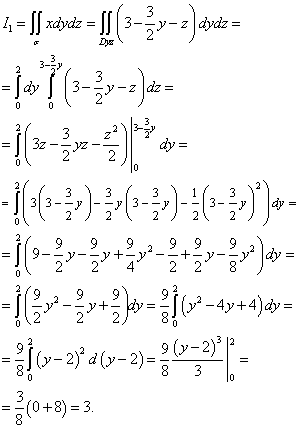
لحساب التكامل أنا2 ، دعونا نبني إسقاطًا سطحيًا σ الى الطائرة زوكس. الإسقاط هو مثلث شركة نفط الجنوب، والتي يحدها خطوط مستقيمة أو ، س= 0 و ض= 0 . نحسب:
نجمع التكاملين الناتجين ونحصل أخيرًا على هذا التكامل السطحي:
.
مثال 6.حساب التكامل السطحي من النوع الثاني
,
أين σ
- السطح الخارجي للهرم المكون من مستوى 
وتنسيق الطائرات.
مثال 3.3.حساب عمل حقل متجه
أ = 2س 2 ذ أنا – xy 2 ي
من الأصل O إلى النقطة A(1;1)، إذا حدثت الحركة على طول: أ)القطعة المستقيمة؛ ب)أقواس القطع المكافئ. الخامس)الخط المتقطع OBA، حيث B(1;0) (انظر الشكل 3.1).
حل . أ)معادلة الخط المستقيم OA لها الشكل ص=س. يترك س = رفإن معادلة الخط المستقيم في الصورة البارامترية سوف تأخذ الصورة:
س = ر، ص = ر،
وعند الانتقال من A إلى B المعلمة رسوف يتغير من 0 إلى 1. ثم سيكون العمل المنجز مساوياً لـ
ب)يترك س = ر 2 , ص = ر، ثم
س = ر 2 ، ص = ر، 0£ ر 1 جنيه استرليني .
.
الخامس)معادلة الخط (OB) هي ذ=0 (0 جنيه استرليني س 1 جنيه استرليني)؛ معادلة الخط (BA) لها الشكل س=1 (0 جنيه استرليني ذ 1 جنيه استرليني). ثم
, 
.
ونتيجة لذلك، نحصل على،
.
تعليق. إذا كان في حالة الحقول ثنائية الأبعاد يتم وصف المعادلة الخطية بالمعادلة ذ=ذ(س)، والمتغير x يختلف من أقبل ب، فسيتم حساب التكامل المنحني للثاني بالصيغة:
. (3.9)
يمكن حل المثال السابق باستخدام هذه الصيغة دون إدخال المعلمة ر.
مثال 3.4.حساب التكامل
,
حيث L هو قوس القطع المكافئ ص=س 2 +1 من النقطة أ(0;1) إلى النقطة ب(2;5).
حل . لنقم بعمل رسم (انظر الشكل 3.2). من معادلة القطع المكافئ نحصل عليه ذ"=2x. منذ على قوس القطع المكافئ أ.بعامل سيتغير من 0 إلى 2، فإن التكامل المنحني، وفقا للصيغة (3.9)، سوف يأخذ الشكل
4. التكاملات السطحية
4.1. التكاملات السطحية من النوع الأول
التكامل السطحي من النوع الأول هو تعميم للتكامل المزدوج ويتم تقديمه بطريقة مماثلة. النظر في بعض السطح س، سلس أو سلس، ونفترض أن الدالة f( س، ص، ض) محددة ومحدودة على هذا السطح. دعونا نقسم هذا السطح إلى نأجزاء تعسفية. يُشار إلى مساحة كل قطعة أرض بالرمز D ق ط. في كل قسم نختار نقطة ذات إحداثيات ( س ط ,ذ ط ,ض ط) وحساب قيمة الوظيفة عند كل نقطة من هذا القبيل. بعد ذلك نقوم بإنشاء المجموع التكاملي:
.
إذا كان هناك حد للمبالغ المتكاملة في ن®¥ (في هذه الحالة الحد الأقصى د ق ط®0)، أي. ومثل هذه النهاية لا تعتمد على طريقة التقسيم ولا على اختيار نقاط الوسط، فتسمى هذه النهاية التكامل السطحي من النوع الأول :
. (4.1)
إذا كانت الدالة f( س، ص، ض) مستمر على السطح س، إذن الحد (4.1) موجود.
إذا كانت الدالة التكاملية f( س، ص، ض)°1 فإن تكامل السطح من النوع الأول يساوي مساحة السطح س:
. (4.2)
لنفترض أنه تم إدخال نظام الإحداثيات الديكارتية، وأي خط مستقيم موازي للمحور أوز،يمكن أن تعبر السطح سعند نقطة واحدة فقط. ثم المعادلة السطحية سيمكن كتابتها في النموذج
ض = ض(س، ص)
ويتم عرضه بشكل فريد على الطائرة xOy. ونتيجة لذلك، يمكن التعبير عن التكامل السطحي من النوع الأول بدلالة التكامل المزدوج
.
(4.3)
مثال 4.1.حساب التكامل
,
أين س– جزء من السطح المخروطي ض 2 =س 2 +ذ 2.0 جنيه إسترليني ض 1 جنيه استرليني.
حل. لدينا
ثم يتم تحويل التكامل المطلوب إلى تكامل مزدوج
أين س س ص- دائرة س 2 +ذ 2 جنيه استرليني 1. لهذا
.
4.2. التكاملات السطحية من النوع الثاني
السماح بتحديد حقل متجه في بعض المناطق
أ = فأس أنا + ذ ي + أ ض ك
وأي سطح على الوجهين س. دعونا نقسم السطح بطريقة ما إلى مناطق أولية د س ط. في كل موقع نختار نقطة تعسفية P أناوتكوين المجموع التكاملي:
, (4.4)
أين ن (باي) - المتجه الطبيعي لسطح معين عند نقطة ما باي. إذا كان هناك حد لمثل هذا المبلغ تحت D س ط®0، ثم يتم استدعاء هذا الحد التكامل السطحي من النوع الثاني (أو تدفق حقل شعاعي أ من خلال السطح س) ويشار إليه بالرمز
أو ،
أين د س =ن س.
نظرًا لأن المتجه العادي للوحدة له جيب التمام الاتجاهي كإحداثيات له ن =(كوسا، cosb، cosg). الذي - التي
وبالتالي يمكن اختزال حساب التكاملات السطحية من النوع الثاني إلى حساب التكاملات السطحية من النوع الأول. ومع ذلك، ماذا على عكس التكاملات السطحية من النوع الأول، تعتمد التكاملات من النوع الثاني على اختيار جانب السطح. الانتقال إلى الجانب الآخر من السطح يغير اتجاه العمودي على السطح، وبالتالي إشارة التكامل.
النظر في التكامل
.
دع المعادلة السطحية لها الشكل ض=ي( س، ص) وسيعتبر الجانب الموجب من هذا السطح هو الذي تكون أشكاله الطبيعية مع المحور O ضزاوية حادة. ثم
com.cosg س = com.dxdy.
لذلك، يمكن كتابة التكامل قيد النظر في الصورة
.
استبدال ضبواسطة ي( س، ص)، وصلنا إلى التكامل المزدوج
,
أين س س ص- الإسقاط السطحي سالى الطائرة xOy.
