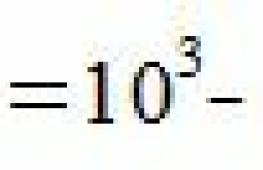Shumëzoni një numër kompleks me konjugatin e tij. Numrat kompleksë dhe veprimet algjebrike mbi to

10.10.2019

Konsideroni një ekuacion kuadratik.

Le të përcaktojmë rrënjët e saj.

Nuk ka numër real, katrori i të cilit është -1. Por nëse operatorin e përkufizojmë me një formulë i si njësi imagjinare, atëherë zgjidhja e këtij ekuacioni mund të shkruhet si . Ku Dhe - numrat kompleks në të cilët -1 është pjesa reale, 2 ose në rastin e dytë -2 është pjesa imagjinare. Pjesa imagjinare është gjithashtu një numër real. Pjesa imagjinare e shumëzuar me njësinë imagjinare do të thotë tashmë numër imagjinar.

NË pamje e përgjithshme një numër kompleks ka formën

z = x + iy ,

Ku x, y– numra realë, – njësi imagjinare. Në një numër shkencash të aplikuara, për shembull, në inxhinierinë elektrike, elektronikë, teorinë e sinjalit, njësia imagjinare shënohet me j. Numrat realë x = Re(z) Dhe y =Une jam(z) quhen pjesë reale dhe imagjinare numrat z. Shprehja quhet formë algjebrike shkrimi i një numri kompleks.

Çdo numër real është një rast i veçantë i një numri kompleks në formë . Një numër imagjinar është gjithashtu një rast i veçantë i një numri kompleks .

Përkufizimi i grupit të numrave kompleks C

Kjo shprehje lexohet si më poshtë: vendos ME, i përbërë nga elementë të tillë që x Dhe y i përkasin bashkësisë së numrave realë R dhe është një njësi imagjinare. Vini re se, etj.

Dy numra kompleks Dhe janë të barabarta nëse dhe vetëm nëse pjesët e tyre reale dhe imagjinare janë të barabarta, d.m.th. Dhe .

Numrat dhe funksionet komplekse përdoren gjerësisht në shkencë dhe teknologji, në veçanti, në mekanikë, analiza dhe llogaritje të qarqeve të rrymës alternative, elektronikën analoge, në teorinë dhe përpunimin e sinjaleve, në teorinë e kontrollit automatik dhe shkenca të tjera të aplikuara.

Aritmetika e numrave kompleks

Mbledhja e dy numrave kompleks konsiston në mbledhjen e pjesëve reale dhe imagjinare të tyre, d.m.th.

Prandaj, diferenca e dy numrave kompleks

Numri kompleks thirrur në mënyrë gjithëpërfshirëse konjuguar numri z =x+iy.

Numrat komplekse të konjuguar z dhe z * ndryshojnë në shenjat e pjesës imagjinare. Është e qartë se

Çdo barazi midis shprehjeve komplekse mbetet e vlefshme nëse kudo në këtë barazi i zëvendësohet nga - i, d.m.th. shkoni te barazia e numrave të konjuguar. Numrat i Dhe – i janë të padallueshme algjebrike, pasi .

Prodhimi (shumëzimi) i dy numrave kompleks mund të llogaritet si më poshtë:

Ndarja e dy numrave kompleks:

Shembull:

Aeroplan kompleks

Një numër kompleks mund të paraqitet grafikisht në një sistem koordinativ drejtkëndor. Le të përcaktojmë një sistem koordinativ drejtkëndor në rrafsh (x, y).

Në bosht kau do të vendosim pjesët reale x, quhet bosht real (real)., në bosht Oy-pjesë imagjinare y numra komplekse. Quhet bosht imagjinar. Në këtë rast, çdo numër kompleks korrespondon me një pikë të caktuar në aeroplan, dhe një plan i tillë quhet plan kompleks. Pika A rrafshi kompleks do t'i përgjigjet vektorit OA.

Numri x thirrur abshissa numër kompleks, numër y – ordinator.

Një çift numrash komplekse të konjuguar përfaqësohet nga pika të vendosura në mënyrë simetrike rreth boshtit real.

Nëse në aeroplan vendosëm sistemi i koordinatave polar, pastaj çdo numër kompleks z përcaktuar nga koordinatat polare. Ku modul numrat është rrezja polare e pikës dhe këndi - argumenti i këndit të tij polar ose numrit kompleks z.

Moduli i një numri kompleks gjithmonë jo negative. Argumenti i një numri kompleks nuk përcaktohet në mënyrë unike. Vlera kryesore e argumentit duhet të plotësojë kushtin . Çdo pikë e planit kompleks gjithashtu korrespondon me vlerën e përgjithshme të argumentit. Argumentet që ndryshojnë me një shumëfish të 2π konsiderohen të barabarta. Argumenti i numrit zero është i papërcaktuar.

Vlera kryesore e argumentit përcaktohet nga shprehjet:

Është e qartë se

Ku
, .

Paraqitja e numrave kompleks z si

thirrur formë trigonometrike numër kompleks.

Shembull.

Forma eksponenciale e numrave kompleks

Zbërthimi në Seria Maclaurin për funksionet e argumentit real ka formën:

Për një funksion eksponencial me një argument kompleks z zbërthimi është i ngjashëm

Zgjerimi i serisë Maclaurin për funksionin eksponencial të argumentit imagjinar mund të përfaqësohet si

Identiteti që rezulton quhet formula e Euler-it.

Për një argument negativ ka formën

Duke kombinuar këto shprehje, mund të përcaktoni shprehjet e mëposhtme për sinusin dhe kosinusin

Duke përdorur formulën e Euler-it, nga forma trigonometrike e paraqitjes së numrave kompleks

në dispozicion tregues formë (eksponenciale, polare) e një numri kompleks, d.m.th. përfaqësimi i saj në formë

Ku - koordinatat polare të një pike me koordinata drejtkëndore ( x,y).

Konjugati i një numri kompleks shkruhet në formë eksponenciale si më poshtë.

Për formën eksponenciale, është e lehtë të përcaktohen formulat e mëposhtme për shumëzimin dhe pjesëtimin e numrave kompleks

Kjo do të thotë, në formë eksponenciale, prodhimi dhe ndarja e numrave kompleksë është më e thjeshtë se në formën algjebrike. Gjatë shumëzimit, modulet e faktorëve shumëzohen dhe argumentet shtohen. Ky rregull zbatohet për çdo numër faktorësh. Në veçanti, kur shumëzoni një numër kompleks z në i vektor z rrotullohet në të kundërt të akrepave të orës 90

Në pjesëtim, moduli i numëruesit ndahet me modulin e emëruesit dhe argumenti i emëruesit zbritet nga argumenti i numëruesit.

Duke përdorur formën eksponenciale të numrave kompleks, mund të marrim shprehje për identitetet e njohura trigonometrike. Për shembull, nga identiteti

duke përdorur formulën e Euler-it mund të shkruajmë

Duke barazuar pjesët reale dhe imagjinare në këtë shprehje, marrim shprehje për kosinusin dhe sinusin e shumës së këndeve

Fuqitë, rrënjët dhe logaritmet e numrave kompleksë

Ngritja e një numri kompleks në një fuqi natyrore n prodhuar sipas formulës

Shembull. Le të llogarisim .

Le të imagjinojmë një numër në formë trigonometrike

’

Duke zbatuar formulën e fuqizimit, marrim

Duke vënë vlerën në shprehje r= 1, marrim të ashtuquajturën formula e Moivre, me të cilin mund të përcaktoni shprehjet për sinuset dhe kosinuset e këndeve të shumta.

Rrënja n-fuqia e një numri kompleks z Ajo ka n vlera të ndryshme të përcaktuara nga shprehja

Shembull. Le ta gjejmë.

Për ta bërë këtë, ne shprehim numrin kompleks () në formë trigonometrike

Duke përdorur formulën për llogaritjen e rrënjës së një numri kompleks, marrim

Logaritmi i një numri kompleks z- ky është numri w, per cilin . Logaritmi natyror i një numri kompleks ka një numër të pafund vlerash dhe llogaritet me formulën

Përbëhet nga një pjesë reale (kosinus) dhe një pjesë imagjinare (sinus). Ky tension mund të përfaqësohet si një vektor i gjatësisë Um, faza fillestare (këndi), rrotulluese me shpejtësi këndore ω .

Për më tepër, nëse shtohen funksione komplekse, atëherë shtohen pjesët e tyre reale dhe imagjinare. Nëse një funksion kompleks shumëzohet me një funksion konstant ose real, atëherë pjesët reale dhe imagjinare të tij shumëzohen me të njëjtin faktor. Diferencimi/integrimi i një funksioni kaq kompleks zbret në diferencimin/integrimin e pjesëve reale dhe imagjinare.

Për shembull, diferencimi i shprehjes komplekse të stresit

është ta shumëzosh atë me iω është pjesa reale e funksionit f(z), dhe – pjesë imagjinare e funksionit. Shembuj: .

Kuptimi z përfaqësohet nga një pikë në rrafshin kompleks z dhe vlera përkatëse w- një pikë në planin kompleks w. Kur shfaqet w = f(z) linjat e avionit z shndërrohen në vija të rrafshët w, figurat e një rrafshi në figura të një tjetri, por format e vijave ose figurave mund të ndryshojnë ndjeshëm.