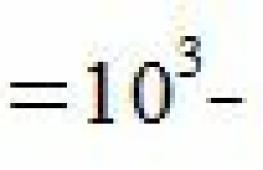Remember these formulas. Remember these formulas Calculating the length of the edges of a cube
Remember these formulas! The sum of the lengths of all edges of a rectangular parallelepiped l=4(a+b+c) ; The sum of the lengths of all edges of the cube l=12a;
Picture 8 from the presentation “Volume of a rectangular parallelepiped” for geometry lessons on the topic “Volume”Dimensions: 960 x 720 pixels, format: jpg.
To download a free image for a geometry lesson, right-click on the image and click “Save image as...”.To display pictures in the lesson, you can also download for free the presentation “Volume of a rectangular parallelepiped.ppt” in its entirety with all the pictures in a zip archive. The archive size is 781 KB.
Download presentation
Volume
“Volume of a rectangular parallelepiped” - Squares. 5. A cube has all equal edges. (Geometric figure). BLITZ - SURVEY (Part I). E. 4. A parallelepiped has 8 edges. 12. Volume of a rectangular parallelepiped. G. F. +. (Flat, volumetric). BF, CG, DH. 3.
“Volume of a parallelepiped” - In Ancient Babylon, cubes served as units of volume. So what is volume? Task No. 1. Find the volume of a cube whose edge is 3 cm. A unit of volume equal to 1 dm3 is called a liter. We are doing the same now. Mathematics teacher I.V. Dymova. Even in ancient times, people needed to measure the quantities of certain substances.
“Rectangular parallelepiped” - Length Width Height. Rectangular parallelepiped. Ribs. Municipal educational institution "Gymnasium" No. 6. Peaks. Parallelepiped. The faces of a parallelepiped that do not have common vertices are called opposite. The parallelepiped has 8 vertices and 12 edges. A parallelepiped is a hexagon, all of whose faces (bases) are parallelograms.
“Calculating the volume of a parallelepiped” - 4. Volume of a rectangular parallelepiped. 2. Task 1: Calculate the volumes of the figures. 3. 1. Mathematics 5th grade.
“Lesson Rectangular parallelepiped” - C1. Objective of the lesson: A. Edges. 8. Oral counting. A1. D1. 12. D. Rectangular parallelepiped. S. Ribs. 6. Peaks.
There are often problems in which it is necessary to find the edge of a cube; often this should be done on the basis of information about its volume, the area of a face or its diagonal. There are several options for defining the edge of a cube.
If the area of the cube is known, then the edge can be easily determined. The face of a cube is a square with a side equal to the edge of the cube. Accordingly, its area is equal to the square of the edge of the cube. You should use the formula: a = √S, where a is the length of the edge of the cube, and S is the area of the face of the cube.





Once again, using the Pythagorean theorem (a^2+a^2=b^2), we can obtain the following relationship: a^2+a^2+a^2=c^2, from which we deduce: 3*a^2=c ^2, therefore, the edge of the cube can be obtained as follows: a=√(c^2/3). A cube is a polyhedron of regular shape with faces of the same shape and size, which are squares. It follows from this that both for its construction and for calculating all related parameters it is enough to know just one value. Using it you can find the volume, the area of each face, the area of the entire surface, length A cube is a polyhedron of regular shape with faces of the same shape and size, which are squares. It follows from this that both for its construction and for calculating all related parameters it is enough to know just one value. Using it you can find the volume, the area of each face, the area of the entire surface, diagonals, ribs or amount lengths of all edges.
Cuba
Instructions A cube is a polyhedron of regular shape with faces of the same shape and size, which are squares. It follows from this that both for its construction and for calculating all related parameters it is enough to know just one value. Using it you can find the volume, the area of each face, the area of the entire surface, Count the number of edges in a cube. This three-dimensional figure has six faces, which determines its other name - regular hexahedron (hexa means “six”). A figure with six square faces can only have twelve edges. Since all the faces are squares of the same size, the lengths of all the edges are equal. This means that to find the total length of all edges, you need to find out
one rib and increase it twelve times. A cube is a polyhedron of regular shape with faces of the same shape and size, which are squares. It follows from this that both for its construction and for calculating all related parameters it is enough to know just one value. Using it you can find the volume, the area of each face, the area of the entire surface, Multiply lengths of all edges one rib A cube is a polyhedron of regular shape with faces of the same shape and size, which are squares. It follows from this that both for its construction and for calculating all related parameters it is enough to know just one value. Using it you can find the volume, the area of each face, the area of the entire surface,(A) by twelve to calculate lengths of all edges all ribs
(L): L=12&lowast-A. This is the simplest possible way to determine the total length of the edges of a regular hexahedron. lengths of all edges If the length of one edge A cube is a polyhedron of regular shape with faces of the same shape and size, which are squares. It follows from this that both for its construction and for calculating all related parameters it is enough to know just one value. Using it you can find the volume, the area of each face, the area of the entire surface, one edge can be expressed as the square root of one sixth of the surface area. To find the length of all edges (L), the value obtained in this way must be increased twelve times, which means that in general the formula will look like this: L=12&lowast-&radic-(S/6).
If the volume is known lengths of all edges(V), then A cube is a polyhedron of regular shape with faces of the same shape and size, which are squares. It follows from this that both for its construction and for calculating all related parameters it is enough to know just one value. Using it you can find the volume, the area of each face, the area of the entire surface, one of its faces can be defined as the cube root of this known quantity. Then A cube is a polyhedron of regular shape with faces of the same shape and size, which are squares. It follows from this that both for its construction and for calculating all related parameters it is enough to know just one value. Using it you can find the volume, the area of each face, the area of the entire surface, all faces (L) of a regular tetrahedron will be twelve cube roots of a known volume: L=12&lowast-?&radic-V.
If the length of the diagonal is known lengths of all edges(D), then to find one edge this value must be divided by the square root of three. The length of all edges (L) in this case can be calculated as the product of the number twelve and the quotient of the diagonal length divided by the root of three: L=12&lowast-D/&radic-3.
If the length of the radius of the sphere inscribed in the cube (r) is known, then the length of one face will be equal to half of this value, and the total length of all edges (L) will be this value, increased six times: L=6&lowast-r.
If the length of the radius of a circumscribed rather than inscribed sphere (R) is known, then the length of one edge will be determined as the quotient of twice the length of the radius divided by the square root of three. Then the length of all edges (L) will be equal to twenty-four radius lengths divided by the root of three: L=24&lowast-R/&radic-3.
Method 1 of 3: Cube the edge of a cube
- Find the length of one edge of the cube. As a rule, the length of a cube edge is given in the problem statement. If you
calculate the volume of a real cubic object, measure its edge with a ruler or tape measure.
Let's consider example. The edge of the cube is 5 cm. Find the volume of the cube.
Cube the length of the edge of the cube. In other words, multiply the length of the edge of the cube by itself three times.
If s is the length of the edge of the cube, then
and thus you will calculate cube volume.
This process is similar to the process of finding the area of the base of a cube (equal to the product of the length times
width of the square at the base) and then multiplying the area of the base by the height of the cube (that is,
in other words, you multiply the length by the width by the height). Since in a cube the length of an edge is equal to the width and
equal to the height, then this process can be replaced by raising the edge of the cube to the third power.
In our example cube volume is equal to:
![]()
- Add volume units to your answer. Since volume is a quantitative
characteristic of the space occupied by a body, then the units of volume measurement are cubic
units (cubic centimeters, cubic meters, etc.).
In our example, the size of the edge of the cube was given in centimeters, so the volume will be measured in cubic
centimeters (or cm 3). So, the volume of the cube is 125 cm3.
If the size of the edge of a cube is given in other units, then the volume of the cube is measured in the corresponding
cubic units.
For example, if the edge of a cube is 5 m (and not 5 cm), then its volume is 125 m 3.
Method 2 of 3: Calculate volume from surface area
- In some problems, the length of the edge of the cube is not given, but other quantities are given with the help of which you
you can find the edge of the cube and its volume. For example, if you are given the surface area of a cube, then divide
it by 6, take the square root from the resulting value and you will find the length of the edge of the cube. Then
Raise the length of the edge of the cube to the third power and calculate the volume of the cube.
Surface area of a cube equal to 6s 2,
Where s - cube edge length(that is, you find the area of one face of the cube and then multiply it by 6, so
like a cube has 6 equal sides).
Let's consider example. The surface area of the cube is 50 cm2. Find the volume of the cube.
- Divide the surface area of the cube by 6 (since the cube has 6 equal sides, you get the area
one face of the cube). In turn, the area of one face of the cube is equal to s 2, Where s- length of the edge of the cube.
In our example: 50/6 = 8.33 cm 2 (remember that area is measured in square units - cm 2,
m 2, etc.).
- Since the area of one face of a cube is s 2, then take the square root of the area value
one face and get the length of the edge of the cube.
In our example, √8.33 = 2.89 cm.
- Cube the resulting value to find the volume of the cube.
In our example: 2.89 * 2.89 * 2.89 = 2.893 = 24.14 cm3. Don't forget to add cubic to your answer.
units.
Method 3 of 3: Calculate Volume Diagonally
- Divide the diagonal of one of the cube's faces by √2 to find the length of the cube's edge. Thus,
if the problem is given the diagonal of a face (any) of a cube, then you can find the length of the edge of the cube by dividing
diagonal by √2.
Let's consider example. The diagonal of the cube's face is 7 cm. Find the volume of the cube. In this case, the length of the cube edge
equal to 7/√2 = 4.96 cm. The volume of the cube is 4.963 = 122.36 cm 3.
Remember: d2 = 2s2,
Where d- diagonal of the cube face, s - edge of the cube. This formula follows from Pythagorean theorem, according to
which the square of the hypotenuse (in our case, the diagonal of the cube face) of a right triangle is equal to
the sum of the squares of the legs (in our case, the edges), that is:
d 2 = s 2 + s 2 = 2s 2.
- Divide the cube's diagonal by √3 to find the length of the cube's edge. Thus, if in the problem
given the diagonal of a cube, then you can find the length of the edge of the cube by dividing the diagonal by √3.
Diagonal of a cube- a segment connecting two vertices that are symmetrical relative to the center of the cube, equal to
D2 = 3s2
(Where D- diagonal of the cube, s- edge of the cube).
This formula follows from the Pythagorean theorem, according to which the square of the hypotenuse (in our case
the diagonal of the cube) of a right triangle is equal to the sum of the squares of the legs (in our case, one leg is
this is an edge, and the second leg is the diagonal of the cube face, equal to 2s 2), that is
D 2 = s 2 + 2s 2 = 3s 2.
Let's consider example. The diagonal of the cube is 10 m. Find the volume of the cube.
D2 = 3s2
10 2 = 3s 2
100 = 3s 2
33.33 = s 2
5.77 m = s
The volume of the cube is 5.773 = 192.45 m3.
“Calculating the volume of a parallelepiped” - 2. Volume of a rectangular parallelepiped. Task 1: Calculate the volumes of the figures. 1. Mathematics 5th grade. 3. 4.
“Rectangular parallelepiped grade 5” - What is volume? Rectangular parallelepiped. Another formula for the volume of a rectangular parallelepiped. Volume of a rectangular parallelepiped. Formula for the volume of a cube. Example. Volume of a cube. Vershin - 8. Mathematics, 5th grade Logunova L.V. Ribs - 12. Cube. Cubic centimeter. The edge of the cube is 5 cm. There are 6 faces.
“Lesson Rectangular parallelepiped” - 12. C1. IN 1. Length. Parallelepiped. Peaks. Ribs. A1. Width. D. Edges. D1. 8. B. Rectangular parallelepiped.
“Volume of a parallelepiped” - So, according to the rule for calculating volume, we get: 3x3x3=27 (cm3). Even in ancient times, people needed to measure the quantities of certain substances. Volumes of liquids and solids are usually measured in liters. In Ancient Babylon, cubes served as units of volume. Now let's define what volume units are? Lesson topic: Volume of a parallelepiped.
“Rectangular parallelepiped” - Parallelepiped. Rectangular parallelepiped. Municipal educational institution "Gymnasium" No. 6. The word was found among the ancient Greek scientists Euclid and Heron. The work was completed by Alina Mendygalieva, a student of class 5 “B”. Length Width Height. A parallelepiped is a hexagon, all of whose faces (bases) are parallelograms. Peaks. The faces of a parallelepiped that do not have common vertices are called opposite.
“Volume of a rectangular parallelepiped” - Edges. 3. BLITZ – SURVEY (Part I). A, c, c, d. Volumetric. Which edges are equal to edge AE? AE, EF, EH. 1. Any cube is a rectangular parallelepiped. Squares. 5. A cube has all equal edges. 8. Rectangle. 12. 3. All faces of a cube are squares. Name the edges that have vertex E.
“Lesson Rectangular parallelepiped” - C1. Objective of the lesson: A. Edges. 8. Oral counting. A1. D1. 12. D. Rectangular parallelepiped. S. Ribs. 6. Peaks.