MA. Oberflächenintegrale zweiter Art

Theoretisches Minimum

Dieses Thema setzt die Diskussion über krummlinige Integrale und Oberflächenintegrale fort, die im Thema „“ begonnen wurde. Es empfiehlt sich, sich vorab mit diesem Thema vertraut zu machen. Aufgrund der größeren Komplexität des Themas, krummlinige und Oberflächenintegrale
die zweite Art wird gesondert betrachtet. Hier werden Oberflächenintegrale der zweiten Art besprochen – vielleicht die komplexeste Integraloperation überhaupt
Analyse der Funktionen vieler Variablen. Der Plan wird der Betrachtung eines krummlinigen Integrals zweiter Art völlig ähnlich sein. Beginnen wir mit physikalischen Anwendungen,
und dann kommen wir zum formalen mathematischen Aspekt.

1. Physikalische Anwendungen des Oberflächenintegrals zweiter Art

Der natürlichste Weg, ein Oberflächenintegral zweiter Art einzuführen, besteht darin, den Fluss einer Flüssigkeit durch eine Oberfläche zu betrachten. Beginnen wir mit einem einfachen Fall:
Die Flüssigkeit fließt mit konstanter Geschwindigkeit entlang der x-Achse. Wählen wir einen Bereich senkrecht zur Strömung aus und ermitteln wir die durchströmende Flüssigkeitsmasse
sie rechtzeitig. In dieser Zeit entstand ein „Parallelepiped“ mit einer Höhe und Grundfläche von . Die Masse dieses „Parallelepipeds“
gleich , wo ist die Dichte der Flüssigkeit.

Lassen Sie nun die Flüssigkeit parallel zur Ebene in einem Winkel zur x-Achse fließen, aber immer noch mit einer Geschwindigkeit. Die Seite von vorhin
In diesem Fall platzieren wir es immer noch senkrecht zur Abszissenachse. Im Laufe der Zeit verläuft ein geneigtes „Parallelepiped“ durch es (siehe Abb. 1). Seine Masse
gleich . Beachten Sie, dass die Einführung eines Einheitsnormalenvektors in die Site das Schreiben ermöglicht.
Es wird ein formaler Vektor einer Elementarfläche eingeführt, dessen Modul gleich ist und dessen Richtung mit der Richtung des Vektors übereinstimmt
normal für die Website. Dann . Diese Notation ermöglicht es Ihnen, sich keine Gedanken über die Richtung des Fluidgeschwindigkeitsvektors in Bezug auf zu machen
zum Ort.

Es bleibt die Kleinheit der Fläche, durch die die Flüssigkeit fließt, und die Annahme eines konstanten Moduls und einer konstanten Geschwindigkeitsrichtung aufzugeben. Dann
Die Oberfläche ist in kleine Teile unterteilt, innerhalb derer der Geschwindigkeitsvektor als konstant angesehen werden kann. Die durch die Oberfläche strömende Flüssigkeitsmasse beträgt
ist durch die Summe näherungsweise gegeben
.
Die genaue Formel erhält man im Grenzfall der Teilung der Oberfläche in infinitesimale Teile. Der Grenzwert ist ein Flächenintegral zweiter Art:
.
Beim Verfassen dieses Abschnitts wurde ein Fragment des Unterrichtsmaterials eines Lehrers des Fachbereichs Allgemeine Physik verwendet, das dieser im Seminarunterricht verwendete.

2. Definition eines Oberflächenintegrals zweiter Art

Nun zur formalen Konstruktion des Integrals. Aufgrund der Tatsache, dass das Vektorfeld über die Oberfläche integriert ist, ist es sinnvoll zu klären, auf welcher Seite
Oberfläche wird das Integral berechnet (wie bei der Berechnung der Strömung einer Flüssigkeit: Flüssigkeit fließt in die Oberfläche hinein oder fließt aus ihr heraus). Daher wird es besonders spezifiziert
dass die Oberfläche, über die die Integration durchgeführt wird, zweiseitig oder orientierbar sein muss (d. h. das Möbius-Band als Ganzes funktioniert nicht). Oberfläche
sofort orientiert, d.h. eine bestimmte Richtung der Normalen zur Oberfläche wird ausgewählt (wenn beispielsweise das Integral über eine Kugel berechnet wird, dann kann die Normale sein).
von der Kugel oder in die Kugel gerichtet). Die Feldkomponenten sind im allgemeinen Fall Funktionen eines Punktes. Oberfläche der Integration
wird in kleine Teile geteilt, in jedem Teil wird ein Punkt ausgewählt und die Summe gebildet
,
wo ist die Fläche der Projektion des Elements auf die Ebene, ist die Fläche der Projektion dieses Elements auf die Ebene, ist die Fläche
Projektion dieses Elements auf eine Ebene. Wir führen die Summation über alle Elemente durch, in die die Fläche unterteilt ist:

und gehen Sie zum Grenzwert, indem Sie den Durchmesser des größten Teilbereichs auf Null richten. Der Grenzwert ist ein Oberflächenintegral zweiter Art
.


Lassen Sie uns zeigen, wie man dieses Integral auf die Form aus Schritt 1 reduziert. Dazu müssen Sie einen kleinen Exkurs rein geometrischer Natur machen. Lass es sein
Ebene, die die Koordinatenachsen schneidet (siehe Abb. 2). Der im ersten Oktanten liegende Teil dieser Ebene hat eine Fläche von . Sie müssen den Bereich finden
alle drei orthogonalen Projektionen eines bestimmten Teils der Ebene auf Koordinatenebenen. Bekanntlich ist die Projektionsfläche einer Figur gleich dem Produkt der Fläche
die Figur selbst und der Kosinus des Winkels zwischen der Ebene der Figur und der Ebene, auf die sie projiziert wird (siehe Abb. 3). Diese. müssen die Winkel finden, die entstehen
Ebene mit Koordinatenebenen. Der Winkel zwischen zwei Ebenen ist gleich dem Winkel zwischen ihren Normalen. Die zur Ebene senkrechte Einheit besteht aus Komponenten,
Das sind seine Richtungskosinusse. Daher ist der Winkel zwischen der Ebene und der Ebene gleich (siehe Abb. 2) und daher .
Die gleiche Beziehung gilt für infinitesimale Flächen: . Und ähnlich.
Unter Berücksichtigung dieser Beziehungen nimmt das Integral die Form an
.
Diese Form der Aufnahme ist übrigens eher visuell, daher werden wir damit arbeiten.

Durch Umkehren der Richtung der Normalen ändert sich das Vorzeichen des Integrals.

3. Berechnung des Oberflächenintegrals zweiter Art

Nachdem das Integral auf eine Form reduziert wurde, die den Richtungskosinus der Flächennormalen enthält, reduziert sich das Problem im Wesentlichen auf das Schreiben der Einheitsnormalen
mit weiterer Berechnung des Flächenintegrals erster Art. Da es bei diesen Aktionen einige Besonderheiten gibt, schauen wir uns die Berechnung im Detail an
Integrale dieser Art.

Beginnen wir mit dem Fall, dass die Integrationsfläche beispielsweise durch eine explizite Gleichung gegeben ist: . Dann wird der Normalenvektor wie folgt geschrieben:
,
und das Flächenelement
.
Das Oberflächenintegral nimmt daher die folgende Form an:
, (1)
Dabei ist der Bereich der Ebene, in den die Integrationsfläche projiziert wird.

Es kann sein, dass die Integrationsfläche korrekt auf die Ebene projiziert wird (und durch die Gleichung gegeben ist) oder auf die Ebene
(und ist durch die Gleichung gegeben ). Dann wird die Formel, nach der das Integral berechnet wird, leicht angepasst:
(2)
oder
. (3)
Natürlich ist es nicht empfehlenswert, solche Formeln auswendig zu lernen: Es ist leicht, etwas zu verwechseln – es ist besser, sie in Bezug auf eine bestimmte Formel wiederherzustellen
erneute Berechnung, basierend auf der Formel für den Normalenvektor und die Fläche eines kleinen Flächenelements.

Es gibt einen hervorgehobenen Fall, wenn die Oberfläche korrekt auf alle drei Koordinatenebenen projiziert wird, d. h. aus der Oberflächengleichung eine beliebige Variable
eindeutig ausgedrückt werden kann. Dann wird die Berechnung deutlich vereinfacht. Achten Sie auf den Aufbau der Formeln (1) – (3). In jedem von ihnen gibt es drei
Begriffe, und einer von ihnen sieht einfacher aus als die anderen. Bei der Projektion einer Fläche auf eine Ebene enthält dieser Begriff die Komponente
Felder; projiziert auf eine Ebene ist dies der Begriff, der die Komponente enthält; projiziert auf eine Ebene ist dies der Begriff
enthaltende Komponente. Wenn die Oberfläche korrekt auf eine beliebige Koordinatenebene projiziert wird, teilen wir das Integral auf
Teilen Sie es in drei Teile auf und gestalten Sie jeden Teil auf die bequemste Art und Weise:
.

Schließlich der Fall der parametrischen Definition der Oberfläche
.
Wie bei der Berechnung eines Oberflächenintegrals erster Art müssen drei Jacobi-Funktionen berücksichtigt werden:
.
Durch sie werden die Richtungskosinusse der Normalen ausgedrückt:
,
Oberflächenelement
.
Somit erhalten wir für das Integral
,
Wo ist der Bereich der Parameteränderungen, der der Integrationsfläche entspricht?

4. Stokes-Formel. Ostrogradsky-Gauss-Formel

Dem Oberflächenintegral zweiter Art sind zwei Formeln zugeordnet, die verschiedene Anwendungen finden, auch in physikalischen Anwendungen.
Stokes-Formel:
,
Wo ,
Die Fläche wird über die Kontur gedehnt, die Durchquerung der Kontur steht im Einklang mit der Wahl der Flächennormalen nach der Rechtsschraubenregel.
Wenn die Integrationsfläche „Löcher“ aufweist, sind Abklärungen erforderlich.
Die Formel von Green ist ein Sonderfall dieser Formel. Darüber hinaus folgt aus der Stokes-Formel die Bedingung für die Unabhängigkeit des krummlinigen Integrals der Sekunde
irgendwie von der Form des Weges.

Ostrogradsky-Gauss-Formel.
Für ein Vektorfeld Die Formel ist erfüllt

wo die Oberfläche das Volumen begrenzt.

Die Ostrogradsky-Gauss-Formel hat verschiedene Anwendungen. Schauen wir uns zwei davon an. Erstens lässt sich leicht beweisen, dass das Volumen eines Körpers berechnet werden kann
nach der Formel

Zweitens ist es manchmal notwendig, ein Flächenintegral zweiter Art über eine offene Fläche zu berechnen, was umständliche Berechnungen erfordert.
Dann wird die Fläche geschlossen, das Integral in ein dreifaches umgewandelt und das Integral über die addierte Fläche subtrahiert (siehe Beispiel unten).

Notiz. Die Stokes- und Ostrogradsky-Gauss-Formeln lassen sich bequemer in der Vektoranalyse unter Verwendung der Curl und Divergenz des Vektorfelds schreiben.

Beispiele zur Berechnung von Oberflächenintegralen zweiter Art

Beispiel 1. Ebenenintegral.. Dann erhalten wir Teile eines elliptischen Paraboloids (äußere Normale).

Schreiben wir das Integral in der Form um
.
Die Integrationsfläche – ein elliptisches Paraboloid – wird nur auf die Ebene korrekt projiziert, daher schreiben wir die Flächengleichung in die Form
.
Finden Sie den Einheitsnormalenvektor:
.

Das Konzept eines Doppelintegrals über einem flachen Bereich lässt sich leicht auf den Fall der Integration über einer Fläche verallgemeinern. Sei (S) eine Fläche (geschlossen oder offen) und eine stetige Funktion eines Punktes auf dieser Fläche. Brechen Sie (S) in Teile

und lassen Sie die Flächen dieser Teile und alle auf diesen Teilen befindlichen Punkte. Zusammenstellen der Summe der Produkte

Der Grenzwert dieser Summe mit unendlicher Zunahme der Teilungszahl und unendlicher Abnahme jedes Teils wird als Integral der Funktion über die Oberfläche bezeichnet

Nehmen wir an, dass gerade Linien parallel zur Z-Achse die Oberfläche nur in einem Punkt schneiden (Abb. 48) und dass die Projektion (S) auf der XOY-Ebene liegt. Mit der Formel (26), die den Zusammenhang zwischen der Elementaroberfläche (S) und der entsprechenden Fläche ihrer Projektion herstellt, können wir das Integral über die Oberfläche (S) auf das Integral über die ebene Fläche reduzieren:

In diesem Fall wird angenommen, dass er von Null verschieden ist und dass der Wert der Funktion am Punkt N der Region mit dem Wert der auf der Oberfläche angegebenen Funktion an diesem Punkt M übereinstimmt, dessen Projektion mit übereinstimmt. Wenn die Gleichung der Oberfläche (S) in expliziter Form (22) angegeben ist und die Funktion durch die Koordinaten ausgedrückt wird, reicht es bei der Integration darüber aus, die Funktion in den Ausdruck einzusetzen. Der Nenner auf der rechten Seite von (29) wird durch die dritte der Formeln (24) bestimmt.

Beachten Sie, dass Oberflächenintegrale offensichtlich alle Eigenschaften eines Doppelintegrals haben, die in angegeben sind, insbesondere gilt für sie der Mittelwertsatz.

Lassen Sie uns nun eine der Hauptformeln in der Theorie der Mehrfachintegrale beweisen – die Ostrogradsky-Formel, die einen Zusammenhang zwischen dem Dreifachintegral über ein Volumen und dem Integral über die Oberfläche (S) herstellt, die dieses Volumen begrenzt. Wir werden überlegen, wie und wo sich Geraden parallel zur Z-Achse in nicht mehr als zwei Fällen (S) schneiden

Punkte. Behalten wir die gleiche Notation wie in Abb. bei. 40. Betrachten wir auch die Richtung der Normalen zu (S) und gehen davon aus, dass sie außerhalb des Volumens (V) gerichtet ist (äußere Normale) (Abb. 50). Diese Richtung bildet mit der OZ-Achse im oberen Teil der Oberfläche (I) einen spitzen Winkel und im unteren Teil (I) einen stumpfen Winkel. Deshalb bemerken wir im unteren Teil, dass auf der Kontaktlinie der Oberfläche (5) mit dem hervorstehenden Zylinder (Abb. 50). Formel (26) ergibt

Sei zusammen mit der Ableitung im Bereich bis (S) stetig. Betrachten wir das dreifache Integral der Funktion. Mit Formel (16) erhalten wir

Aber das Integral der Ableitung ist gleich der Differenz zwischen den Werten der Stammfunktion an der Ober- und Untergrenze:

Durch Ersetzen durch gemäß den Formeln (30) reduzieren wir die Integration auf die Integration über (S), und im ersten Integral, das die variable Ordinate des Teils (I) der Oberfläche (S) enthält, müssen wir die erste der Formeln verwenden (30), und wir erhalten das Integral über (II), im zweiten Integral, das enthält, müssen Sie die zweite der Formeln (30) verwenden, und Sie erhalten das Integral über (I):

Die Symbole für z können nicht mehr geschrieben werden, da angegeben wird, über welchen Teil der Oberfläche die Integration durchgeführt wird. Auf der rechten Seite steht die Summe der Integrale über die Teile (II) und (I), also das Integral über das Ganze

Flächen (S):

Wenn es Funktionen gibt, die die Eigenschaften der Funktion R haben, dann berücksichtigen Sie dies

Basierend auf (31) können wir die Formel für die partielle Integration schreiben:

Auf genau die gleiche Weise könnten wir mit zwei anderen Funktionen beweisen

Wenn wir die drei erhaltenen Formeln Term für Term addieren, erhalten wir Ostrogradskys Formel

Ähnlich wie (31) werden partielle Integrationsformeln für Ableitungen nach x und y geschrieben.

Der Kürze halber schreiben wir hier nicht die Argumente x, y, z der Funktionen P, Q, aber wir müssen bedenken, dass es sich um Funktionen handelt, die im Volumen definiert und mit ihren Ableitungen stetig sind.

Im nächsten Kapitel werden wir zahlreiche Beispiele für die Anwendung der Ostrogradsky-Formel geben.

Größen sind auf der Oberfläche (S) definierte Funktionen. Wir betrachteten sie als kontinuierlich. Man kann eine allgemeinere Annahme treffen, nämlich annehmen, dass (S) in eine endliche Anzahl von Teilen unterteilt ist, auf denen die angegebenen Funktionen jeweils stetig sind. Dies ist beispielsweise der Fall, wenn (S) ein Polyeder ist.

Bei der Ableitung der Formel (31) haben wir angenommen, dass zur Achse parallele Geraden die Oberfläche (S) der Region an nicht mehr als zwei Punkten schneiden. Es ist nicht schwierig, diese Formel auf Bereiche allgemeinerer Form zu übertragen. Beachten wir zunächst, dass, wenn die Fläche (S) zusätzlich zum oberen Teil (II) und dem unteren Teil (I) einen zylindrischen Seitenteil mit zur Achse parallelen Erzeugenden hat, dann auf diesem Seitenteil und hinzufügen Dieser Teil auf der rechten Seite der Formel (31) ändert den Wert des Oberflächenintegrals nicht, sodass der gesamte Beweis der Formel weiterhin gültig bleibt. In einem allgemeineren Fall reicht es aus, Zylinderflächen mit zur Achse parallelen Erzeugenden zu verwenden, um sie in eine endliche Anzahl von Teilen zu unterteilen, die die vorherigen Bedingungen erfüllen, und auf jeden Teil die Formel (31) anzuwenden. Wenn wir die so erhaltenen Formeln addieren, erhalten wir auf der linken Seite ein dreifaches Integral über das gesamte Volumen. Auf der rechten Seite haben wir die Summe der Integrale über alle Oberflächen derjenigen Teile, in die wir (v) unterteilt haben. Die Integrale über die reduzierten Hilfszylinderflächen sind, wie oben angegeben, gleich Null. Als Ergebnis der Addition auf der rechten Seite erhalten wir also ein Integral über die Oberfläche (S) des ursprünglichen Volumens. Es stellt sich also heraus, dass Formel (31) für Domänen einer allgemeineren Form gültig ist.

Betrachten wir Integrale von auf Oberflächen definierten Funktionen, die sogenannten Oberflächenintegrale. Die Theorie der Oberflächenintegrale ähnelt in vielerlei Hinsicht der Theorie der krummlinigen Integrale. Es gibt Oberflächenintegrale des ersten und

der zweiten Art.

4.1. Oberflächenintegrale erster Art. Sei die Funktion f(x, y, z)

definiert auf einer stückweise glatten Oberfläche S, begrenzt durch eine stückweise glatte Kontur (Abb. 4.1). Lassen Sie es uns aufschlüsseln

jeweils ∆ s 1, ∆ s 2 ..., ∆ s n. Wir nehmen einen beliebigen Punkt M i (x i, y i, z i) innerhalb jedes Teils S i, i = 1, n, berechnen den Wert der darin enthaltenen Funktion und bilden die folgende Summe:

σ n= ∑ f (x i, y i, z i) ∆ s i

ich= 1

für die Funktion f (x, y, z) durch

welches man Integral nennt

Oberfläche S.

Die letzte Grenze I davon

beim Streben

das größte λ der Durchmesser aller Teilflächen S i

1, n

Wenn es existiert und weder von der Methode zur Aufteilung der Oberfläche in Teilpunkte noch von der Wahl der Punkte abhängt, wird es aufgerufen Flächenintegral erster Art (über die Fläche) aus der Funktion

f (x, y, z) entlang der Oberfläche S und wird mit dem Symbol bezeichnet

∫∫ f(x, y, z) ds.

Also per Definition

= ∫∫ f(x, y, z) ds.

I = lim ∑ f(xi , yi , zi ) ∆ si

λ → 0i = 1

Das Oberflächenintegral erster Art ist eine Verallgemeinerung des Doppelintegrals, daher lassen sich die Bedingungen für die Existenz des Doppelintegrals und seine Eigenschaften leicht auf das Oberflächenintegral erster Art übertragen.

Berechnung von Oberflächenintegralen erster Art reduziert sich auf die Berechnung von Doppelintegralen: basierend auf der Oberflächengleichung S,

Der Integrand wird in zwei Variablen umgewandelt, deren Bereich die Projektion der Oberfläche S auf die diesen Variablen entsprechende Koordinatenebene ist.

Die Oberfläche S sei durch die Gleichung z = z (x, y) definiert und z (x, y) sei zusammen mit ihren partiellen Ableitungen z ′ x, z ′ y in einem geschlossenen Bereich S xy stetig, der die Projektion von ist die Fläche S auf die Koordinatenebene xOy, dann

∫∫ f(x, y, z) ds= ∫∫ f(x, y, z(x, y)) 1 + (z′ x ) 2 + (z′ y ) dxdy.

S xy

Diese Formel drückt das Flächenintegral erster Art durch das Doppelintegral über die Projektion der Fläche S auf die Koordinatenebene xOy aus.

Flächenintegrale erster Art über die Fläche S werden auf ähnliche Weise durch Doppelintegrale über ihre Projektionen auf berechnet

Koordinatenebenen xOz bzw. yOz:

∫∫ f (x ,y ,z )ds = ∫∫ f (x ,y (x ,z ),z )

1+ (y ′ x )2 + (y ′ z )dxdz ,

S xz

∫∫ f (x, y,z)ds= ∫∫ f (x(y,z), y,z)

1 + (x′ y )2 + (x′ z )dydz.

S yz

Mithilfe von Flächenintegralen erster Art ist es möglich, für Materialoberflächen mit bekannter Oberflächenmassenverteilungsdichte die Oberfläche sowie Masse, statische Momente, Trägheitsmomente und Koordinaten des Massenschwerpunkts zu berechnen.

Beispiel 4.1. Berechnung

∫∫ 1 + 4 x 2 + 4 y 2 ds , wobei S Teil des Parabo-

Rotationsoid z = 1 − x 2 − y 2 , abgeschnitten durch die Ebene z = 0 .

Lösung. Lassen Sie uns die Oberfläche gestalten

S zur Ebene xOy .

Die Projektion S xy ist ein Kreis, der durch den Kreis x 2 + y 2 = 1 begrenzt wird (Abb.

4.2). Wir berechnen das gegebene Oberflächenintegral mit der Formel (4.2), für die wir z ′ x = − 2 x , z ′ y = − 2 y finden. Dann verpflichten Sie sich doppelt

Integral

zum Polar

koordinaten,

S xy ist ein Kreis,

1 +4 x 2 +4 y 2 ds =∫∫

1+ 4x 2 + 4y 2

1 + 4 x2 + 4 y2 dxdy=

S xy

= ∫∫ (1 +4 x 2 +4 y 2 ) dxdy =

S xy

= ∫ d ϕ ∫ (1 +4 ρ 2 ) ρ d ρ =∫

+ ρ 4)

d ϕ=

∫d ϕ .

4.2. Doppelseitige Oberflächen. Die Fläche S heißt

zweiseitig: Wenn Sie entlang einer geschlossenen Kontur fahren, die auf der Oberfläche S liegt und deren Grenzen nicht schneidet, ändert sich bei der Rückkehr zum Startpunkt die Richtung der Normalen zur Oberfläche nicht. Ansonsten heißt die Fläche einseitig. Beispiele für zweiseitige Flächen: Ebene, Kugel und jede Fläche, die durch die Gleichung z = z (x, y) definiert ist, wobei z = z (x, y), z ′ x (x, y), z ′ y (x , y) - kontinuierlich in einem bestimmten BereichG. Ein Beispiel für eine einseitige Fläche ist ein Möbiusband.

4.3. Oberflächenintegral zweiter Art. Lasst uns - glatte Oberfläche, gegeben durch die Gleichung z = z(x, y) und Funktion f(x, y, z)

definiert an Punkten der Oberfläche S.

Wählen wir eine der Seiten der Oberfläche aus, also eine von zwei möglichen Richtungen der Normalen an Punkten der Oberfläche (so haben wir die Oberfläche ausgerichtet). Wenn die Normalen spitze Winkel mit bilden

Oz-Achse , dann werden wir darüber reden die Oberseite der Oberfläche (ungefähr die positive Richtung der Normalen). ), und wenn die Normalen sind – stumpfe Winkel mit der Oz-Achse, dann sprechen wir von der Unterseite der Oberfläche (der negativen Richtung der Normalen).

Teilen wir die Fläche S willkürlich in n Teile S 1, S 2 ..., S n und durch (S xy ) i bezeichnen wir die Projektion des i-ten Teils der Fläche

zur xOy-Ebene. Wählen Sie innerhalb jeder Teilfläche S i , i = 1, n einen beliebigen Punkt M i (x i , y i , z i ) und berechnen Sie den Wert der Funktion

Darin werden wir die Summe bilden

σ n= ∑ f (x i, y i, z i) ∆ s i, i = 1

wobei ∆ s i - Fläche(S xy) i, mit einem Pluszeichen, wenn die Oberseite der Oberfläche S ausgewählt wird, und mit einem Minuszeichen, wenn die Unterseite ausgewählt wird

Oberfläche S. Diese Summeσ n heißt Integralsumme für die Funktion f(x, y, z).

Der endgültige Grenzwert I der Integralsumme als größtes λ aller Projektionsdurchmesser (S xy ) tendiert gegen Null, falls vorhanden und

hängt weder von der Art der Aufteilung der Fläche S noch von der Wahl der Punkte ab

M i (x i, y i, z i), dann heißt dieser Grenzwert Oberflächenintegral des zweiten Funktionstyps f(x, y, z) entlang der ausgewählten Seite der Oberfläche durch Variablen x und y und bezeichnet mit ∫∫ f (x, y, z) dxdy. So, gem

Definition

Oberfläche S in den Variablen x und y.

Ebenso können Sie Flächenintegrale des zweiten Typs über eine ausgewählte Seite der Fläche S in den Variablen y und z, in den Variablen x und z definieren:

∫∫ f(x, y, z) dydz,

∫∫ f(x, y, z) dxdz.

Seien P (x, y, z), Q (x, y, z), R (x, y, z) über integrierbare Funktionen

Oberfläche S in den Variablen y und z, x und z, x und y. Summe der Integrale

∫∫ P(x, y, z) dydz,

∫∫ Q(x, y, z) dxdz,

∫∫ R(x, y, z) dxdy

heißt allgemeines Integral zweiten Typs und wird bezeichnet

∫∫ P(x, y, z) dydz+ Q(x, y, z) dxdz+ R(x, y, z) dxdy.

Da wir die Fläche S als zweiseitig betrachten und sich das Integral auf eine bestimmte Seite davon erstreckt, dann Wenn sich die Seite der Integrationsfläche ändert, ändert das Flächenintegral der zweiten Art das Vorzeichen in das Gegenteil– darin liegt der Unterschied zum Flächenintegral erster Art.

Berechnung von Oberflächenintegralen zweiter Art reduziert sich auf die Berechnung von Doppelintegralen.

Eine orientierte (wählen Sie die Oberseite) glatte Oberfläche S sei durch die Gleichung z = z (x, y) gegeben, wobei z (x, y) stetig in sei

geschlossener Bereich S xy - Projektion der Oberfläche S auf die Ebene xOy; die Funktion f(x, y, z) ist stetig auf S. Dann ist die Formel gültig

∫∫ f(x, y, z) dxdy= ∫∫ f(x, y, z(x, y)) dxdy,

S xy

Ausdrücken des Oberflächenintegrals zweiter Art über die Variablen x und

durch doppelt. Wenn wir die untere Seite der Fläche S wählen, dann vorne

Integral wird auf der rechten Seite ein Minuszeichen angezeigt.

Die Formeln gelten gleichermaßen

∫∫ f(x, y, z) dydz= ∫∫ f(x(y, z), y, z) dydz,

S yz

∫∫ f(x, y, z) dxdz= ∫∫ f(x, y(x, z), z) dxdz,

S xz

wo Oberfläche S

entsprechend den Gleichungen

x = x(y, z)

y = y(x, z) und Syz

und S xz -

Projektionen der Oberfläche S bzw

Ebenen yOz und xOz.

Zur Berechnung des allgemeinen Formintegrals (4.6) werden die Formeln (4.7)–(4.9) verwendet, wenn die Fläche S eindeutig auf alle projiziert wird

Koordinatenebenen. In komplexeren Fällen wird die Oberfläche S in Teile mit den angegebenen Eigenschaften unterteilt und das allgemeine Integral in Form von Integralen über diese Teile dargestellt.

Beispiel 4.2.Berechnen

∫∫ (y 2 + z 2 ) dxdy , wobei S die Oberseite ist

Oberfläche z =

1 − x 2

Abgeschnitten flach

Würfel y = 0, y = 1.

Lösung. Die Gleichung x 2 + z 2 = 1 -

ein Kreiszylinder mit einer Erzeugenden angegeben wird,

parallel zur Oy-Achse und der Ebene y = 0 und

y = 1

parallel

Koordinate

xOz-Ebene (Abb.

Projektion

Fläche S auf der Ebene xOy ist

Rechteck S xy definiert durch die Ungleichungen − 1 ≤ x ≤ 1,

0 ≤ y ≤ 1.

Dann gilt nach Formel (4.7).

∫∫ (y2 + z2 ) dxdy= ∫∫ (y2 + (1 − x2 )) dxdy= ∫ dx∫ (y2 − x2 + 1) dy=

S xy

−1

+ (1− x 2 )y )

= ∫ dx (

−1

− x2 ) dx

= ∫ (

−1

−1

Beispiel 4.3. Berechnung

∫∫ xdydz+ ydxdz+ zdxdy, wobei S das obere ist

Seite eines Teils der Ebene x + z − 1 = 0

abgeschnitten durch Ebenen y = 0, y = 4 und

liegt im ersten Oktanten (Abb. 4.4).

Lösung. Projektion der Fläche S auf

die xOy-Ebene ist das Rechteck S xy,

definiert durch die Ungleichungen 0 ≤ x ≤ 1,

0 ≤ y ≤ 4 . Projektion der Fläche S auf

Die yOz-Ebene ist ein Rechteck

S yz, definiert durch die Ungleichungen

0 ≤ z ≤ 1,0 ≤ y ≤ 4. Da die Ebene S senkrecht zur Ebene steht

xOz , dann∫∫ ydxdz = 0. Dann gilt nach den Formeln (4.7) und (4.9).

∫∫ xdydz+ ydxdz+ zdxdy= ∫∫ (1 − z) dydz+

S yz

+ ∫∫ (1 − x) dxdy= ∫ dy∫ (1 − z) dz+ ∫ dy∫ (1 − x) dx=

S xy

− z )

(1− x)

2 ∫

dy = 4.

= ∫ dy −

+ ∫ dy −

4.4. Ostrogradsky-Formel. Ostrogradskys Formel stellt einen Zusammenhang zwischen dem Flächenintegral über eine geschlossene Fläche und dem Dreifachintegral über den durch diese Fläche begrenzten Raumbereich her.

Sei V ein regelmäßiger geschlossener Bereich, der durch die Oberfläche S begrenzt wird, und seien die Funktionen P(x, y, z), Q(x, y, z), R(x, y, z)

sind zusammen mit ihren partiellen Ableitungen erster Ordnung in einem bestimmten Bereich stetig. Dann gilt folgende Formel:

∫∫∫(

∂P

∂Q

∂ R ) dxdydz= ∫∫ Pdydz+ Qdxdz+ Rdxdy, (4.10)

∂x

∂y

∂z

angerufen Ostrogradskys Formel 1 .

Mit der Ostrogradsky-Formel lassen sich Flächenintegrale über geschlossene Flächen bequem berechnen.

Beispiel 4.4. Berechnen Sie mit der Ostrogradsky-Formel

∫∫ xdydz + ydxdz + zdxdy ,

Wo S

Seite der Pyramide

begrenzt

Flugzeuge

X + j + z = 1,

X= 0,j= 0,

z= 0 (Abb. 4.5).

Entsprechend

Ostrogradsky:

P(X,j,z)= X,Q(X,j,z)= j,R(X,j,z)= z.

Dann: ∂ P+

∂ Q+

∂R

= 1+ 1+ 1= 3,und wir finden

∂X

∂j

∂z

1− X

1 −X−j

∫∫ xdydz + ydxdz + zdxdy = 3 ∫∫∫ dxdydz = 3 ∫ dx ∫ dy

∫ dz =

1− X

1 −X−j

1− X

= 3 ∫ dx ∫ dy ∫ dz = 3 ∫ dx ∫ (1 − X − j ) dy =

j 2

1− X

3 ∫ dx ( j − xy −

−2 X+1

3 (X− 1)

= 3 ∫ (1 −X−X+X2 −

) dx =

∫ ( X − 1) 2 dx =

Bemerkung 4.1. Der Zusammenhang zwischen Flächenintegralen des ersten und zweiten Typs ähnelt dem Zusammenhang zwischen krummlinigen Integralen:

∫∫ F ( X , j , z ) dxdy = ∫∫ F ( X , j , z )cosα ds ,

∫∫ F ( X , j , z ) dydz = ∫∫ F ( X , j , z )cosβ ds ,

∫∫ F ( X , j , z ) dxdz = ∫∫ F ( X , j , z )cosγ ds ,

Wo cosα ,cosβ ,cosγ - Richtungskosinus der Normalen entsprechend

ausgewählte Seite der Oberfläche.

,j)

kontinuierlich in der Gegend Sxy– Oberflächenprojektionen S

zum Flugzeug xOy;L

– Kontur,

einschränkend

Oberfläche

S ; l –

Raumlinienprojektion L zum Flugzeug

xOy ,

Sein

ein Zwinger, der den Bereich begrenzt D. Wählen wir die Oberseite aus

Oberflächen S. Wenn das funktioniert P(X, j, z), Q(X, j, z), R(X, j, z)

kontinuierlich

zusammen mit seinen partiellen Ableitungen erster Ordnung auf

Oberflächen S, dann gilt folgende Formel:

∫ Pdx + Qdy + Rdz =

= ∫∫

(∂ Q

∂ P) dxdy + (

∂R

∂ Q) dydz + (∂ P

∂ R) dxdz

∂X

∂j

∂j

∂z

∂z

∂X

(L- bewegt sich in eine positive Richtung)

angerufen Formel

Wenn als Oberfläche S Bereich einnehmen D auf der Oberfläche xOy

(z= 0 ), dann erhalten wir aus (4.11) die Greensche Formel

∂Q

∂ P) dxdy .

∫ P ( X , j ) dx + Q ( X , j ) dy = ∫∫ (

∂X

∂j

Somit ist die Formel von Green ein Sonderfall der Formel von Stokes.

Beachten Sie, dass das Oberflächenintegral vom zweiten Typ in der Formel ist

Stokes (4.11) kann durch das Oberflächenintegral des ersten ersetzt werden

Typ. Dann wird diese Formel die Form annehmen

∫ Pdx + Qdy + Rdz =

∂Q

∂P

∂R

∂Q

∂P

∂R

= ∫∫

)cos α + (

)cos β + (

)cos γ

∂X

∂j

∂j

∂z

∂z

∂X

ds ,

Wo cos α ,cos β ,cos γ ,

bedeuten

Führer

Kosinus

entsprechend der ausgewählten Seite der Oberfläche.

mit der Formel

Berechnung

∫ X 2 j 3 dx + dy + zdz ,

Kreis,

gegeben durch die Gleichungen

X 2 + j 2 + 1, z = 0 .

Oberfläche S die Oberseite der Halbkugel dient

X 2+ j 2+ z 2= 1,

z> 0 (L geht in eine positive Richtung).

Für Fälle, in denen die Integration nicht über einen Kurvenabschnitt, sondern über eine begrenzte Fläche erfolgt. Oberflächenintegrale sind wie krummlinige Integrale erster und zweiter Art.

Oberflächenintegral erster Art im Formular geschrieben

Wo F(M) = F(x,y,z) ist eine Funktion von drei Variablen und der Oberfläche σ - Integrationsbereich dieser Funktion. Wenn F(x,y,z) gleich Eins ist, dann ist das Oberflächenintegral gleich der Oberfläche.

Stellen Sie sich eine ziemlich große Sonnenblume mit sehr, sehr kleinen Samen vor. Aus der Summe der Oberflächen sehr, sehr kleiner Samen, die sich auf der Oberfläche einer Sonnenblume befinden, kann man dann die Oberfläche der Sonnenblume berechnen – dies ist möglicherweise eine vereinfachte Interpretation des Oberflächenintegrals. Warum so?

Kommen wir zu einer formaleren Definition eines Oberflächenintegrals. Oberfläche σ eingeteilt in N Teile mit Flächen Δ σ 1 , Δ σ 2 , ..., Δ σ N. Wenn Sie auf jeder Teilfläche (Seed) einen beliebigen Punkt auswählen Mich mit Koordinaten ( ζ ich, η ich, ς ich ,), dann können wir zusammenfassen

Diese Summe wird Integralsumme der Funktion genannt F(M) an der Oberfläche σ . Jetzt maximieren wir die Anzahl solcher Kleinteile und den größten Durchmesser Δ σ ich- im Gegenteil, reduzieren. Wenn die Integralsumme als größter Durchmesser der Teile gegen Null geht (d. h., wie bereits erwähnt, sind alle Teile sehr klein) eine Grenze hat, dann heißt diese Grenze Oberflächenintegral erster Art aus der Funktion F(M) an der Oberfläche σ .

Berechnung des Oberflächenintegrals erster Art

Lassen Sie die Oberfläche σ gegeben durch die Gleichung z = z(X, j) , seine Projektion auf die Ebene xOy ist die Gegend Dxy, während die Funktion z = z(X, j) und seine partiellen Ableitungen sind in der Region stetig Dxy.

Beispiel 1.

Wo σ - Teil der Ebene im ersten Oktanten.

Lösung. Zeichnung:

Aus der Ebenengleichung erhalten wir den Ausdruck „zet“: .

Dann sind die partiellen Ableitungen: , und

.

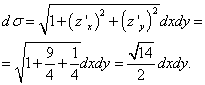Oberfläche σ ist das in der Zeichnung dargestellte Dreieck ABC und seine Projektion auf die Ebene xOy- Dreieck AOB, die durch Geraden begrenzt ist X = 0 , j= 0 und 3 X + j= 6. Gehen wir vom Flächenintegral zum Doppelintegral über und lösen es:

.

Das Konzept eines Oberflächenintegrals zweiter Art

Bevor mit der Definition eines Flächenintegrals zweiter Art fortgefahren wird, ist es notwendig, sich mit den Konzepten von Flächenseiten und orientierten Flächen vertraut zu machen.

Es sei eine glatte Oberfläche im Raum gegeben σ . Wählen wir einen beliebigen Punkt auf dieser Oberfläche M und zeichne den Normalenvektor zur Oberfläche durch ihn hindurch. Durch den Punkt M Wir werden auch an der Oberfläche durchführen σ eine beliebige Kontur, die keine gemeinsamen Punkte mit der Oberflächengrenze hat σ . Punkt M Zusammen mit dem Normalenvektor bewegen wir uns entlang der Kontur, sodass der Normalenvektor ständig senkrecht zur Oberfläche steht σ . Nach Rückgabe des Punktes M Zur Ausgangsposition sind zwei Fälle möglich: Die Richtung des Normalenvektors bleibt gleich oder ändert sich in die entgegengesetzte Richtung.

Wenn sich die Richtung des Normalenvektors nicht ändert, dann ist die Oberfläche σ bilateral genannt. Ändert sich beim Überfahren der Kontur die Richtung des Normalenvektors in die entgegengesetzte Richtung, so heißt die Fläche einseitig. Doppelseitige Flächen werden als orientierte Flächen bezeichnet, einseitige Flächen als unorientierte Flächen.

Ein Beispiel für eine einseitige Oberfläche ist ein Möbius-Streifen (im Bild oben), der aus einem Papierstreifen hergestellt werden kann, dessen eine Seite um 180 Grad gedreht und dessen Enden dann zusammengeklebt werden. Und hier kommt es darauf an: für eine einseitige Fläche wird der Begriff eines Flächenintegrals zweiter Art nicht eingeführt .

Daher betrachten wir nur zweiseitige Flächen. Beispiele für zweiseitige Flächen sind Ebenen, Kugeln, Ellipsoide und Paraboloide.

Die positive Seite einer zweiseitigen Fläche bestimmt die Richtung des Normalenvektors. Die gegenüberliegende Seite der Oberfläche wird als negativ bezeichnet. Die positive Seite einer Fläche ist ihre Oberseite. Wenn die Einheitsnormalenvektoren spitze Winkel mit der Achse bilden Oz, dann wird die Oberseite der Oberfläche ausgewählt z = z(X, j) , wenn die Winkel stumpf sind, dann die Unterseite der Fläche.

Wie beim Flächenintegral erster Art kann die Fläche unterteilt werden in N Teile. Bei der Formulierung des Konzepts eines Oberflächenintegrals erster Art umfasste die Integralsumme die Flächen jedes der Teile, mit denen die Werte der Funktion multipliziert wurden F(Mich). Bei einem Flächenintegral zweiter Art werden nicht die Flächen der Teile selbst genommen, sondern die Flächen ihrer Projektionen auf Koordinatenebenen . Und um die Funktion dreier Variablen von einem Integral erster Art zu unterscheiden, bezeichnen wir R(X,j,z) . Dann wird die Integralsumme wie folgt geschrieben:

,

wobei Δ Sich- die Flächen der erwähnten Projektionen von Teilen der Seite der Oberfläche auf die Koordinatenachse (vorerst gehen wir davon aus, dass auf der Achse). xOy).

Mit solchen Konventionen und Notationen ähnelt die Definition eines Oberflächenintegrals zweiter Art der Definition eines Integrals erster Art. Nämlich: Ein Flächenintegral zweiter Art ist der Grenzwert einer gegebenen Integralsumme, da der größte Durchmesser der betrachteten Flächenteile gegen Null geht.

Es ist so geschrieben:

.

In diesem Fall die Funktion R(X,j,z) über Variablen integrierbar X Und j, da Teile der Oberfläche auf die Ebene projiziert wurden xOy.

Ebenso können wir zwei weitere Oberflächenintegrale zweiter Art schreiben:

(Funktion P(X,j,z) über Variablen integrierbar j Und z yOz),

(Funktion Q(X,j,z) über Variablen integrierbar z Und X, da Teile der Oberfläche auf die Ebene projiziert werden zOx).

Die Summe dieser Integrale

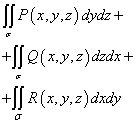
angerufen allgemeines Oberflächenintegral zweiter Art und ist bezeichnet

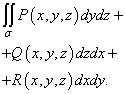
Berechnung des Oberflächenintegrals zweiter Art

Ein Flächenintegral zweiter Art wird berechnet, indem man das allgemeine Flächenintegral zweiter Art in die Summe der Flächenintegrale zerlegt (siehe Ende des vorherigen Absatzes) und diese jeweils auf ein Doppelintegral reduziert.

Betrachten wir die Berechnung des Integrals im Detail

.

Lassen Sie die Oberfläche σ gegeben durch die Gleichung z = z(X, j) . Wir bezeichnen die positive Seite der Oberfläche, die negative Seite und die Projektion auf die Ebene xOy - Dxy.

Somit erhalten wir eine Formel zur Berechnung des Oberflächenintegrals zweiter Art:

Wählt man die negative Seite der Fläche, so ändert sich das Vorzeichen des Integrals:

Die anderen beiden separaten Integrale – Terme des Allgemeinen – werden auf ähnliche Weise berechnet:

Beispiel 2.

,

Wo σ - die Oberseite eines von Hobeln abgeschnittenen Teils des Flugzeugs j= 0 und j= 4 und liegt im ersten Oktanten.

Lösung. Die Zeichnung ist im Bild oben. Per Definition erhalten wir die Summe von drei Doppelintegralen:

Das zweite Integral ist gleich Null, da die Ebene σ parallel zur Achse Oy. Daher finden wir das erste und dritte Integral:

Jetzt müssen nur noch alle Einzelintegrale addiert werden und man erhält das allgemeine Flächenintegral zweiter Art:

.

Wenn Sie ein Oberflächenintegral zweiter Art über eine geschlossene Oberfläche berechnen müssen, können Sie zu gehen Dreifaches Integral, unter Verwendung der Ostrogradsky-Formel. Dann, wenn das funktioniert P(x,y,z) , Q(x,y,z) Und R(x,y,z) und ihre partiellen Ableitungen , , sind stetige Funktionen im Definitionsbereich W, die von einer geschlossenen Fläche begrenzt wird σ , dann bei Integration über die Außenseite der Fläche die Gleichheit

Beispiel 3. Berechnen Sie Flächenintegrale zweiter Art

,

Wo σ - die Außenseite der Oberfläche eines Kegels, der aus einer Oberfläche und einer Ebene besteht z = 2 .

Lösung. Diese Fläche ist die Oberfläche eines Kegels mit einem Radius R= 2 und Höhe H= 2 . Da es sich um eine geschlossene Fläche handelt, können Sie die Formel von Ostrogradsky verwenden. Als P = 3X , Q = 4j , R = −z, dann die partiellen Ableitungen , , .

Wir gehen zum Dreifachintegral über, das wir lösen:

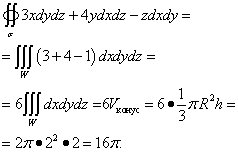
Weitere Beispiele zur Berechnung von Oberflächenintegralen

Beispiel 4. Berechnen Sie Flächenintegrale erster Art

Wo σ - Mantelfläche des Kegels bei .

Lösung. Da die partiellen Ableitungen , , Das

Wir reduzieren dieses Flächenintegral auf ein doppeltes:

Projektion einer Fläche auf eine Ebene xOy ist ein Kreis mit Mittelpunkt im Ursprung und Radius R= 2, daher bewegen wir uns bei der Berechnung des Doppelintegrals zum Polarkoordinatensystem. Dazu ändern wir die Variablen:

Wir erhalten das folgende Integral, das wir schließlich lösen:

Beispiel 5. Berechnen Sie Flächenintegrale zweiter Art

,

Wo σ - der obere Teil des Dreiecks, das durch den Schnittpunkt der Ebene mit den Koordinatenebenen gebildet wird.

Lösung. Teilen wir dieses Flächenintegral durch die Summe zweier Integrale

, Wo

.

Um das Integral zu berechnen ICH1 σ zum Flugzeug yOz. Die Projektion ist ein Dreieck OCB, der sich im Flugzeug befindet yOz gerade Linien begrenzen oder, j= 0 und z= 0 . Aus der Gleichung wird die Ebene abgeleitet. Daher können wir das Integral berechnen ICH1 :

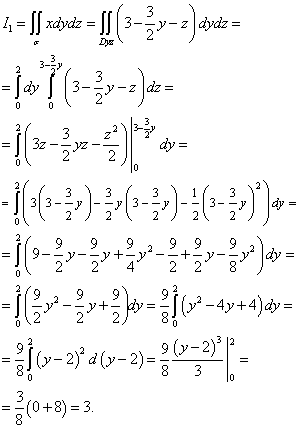
Um das Integral zu berechnen ICH2 , konstruieren wir eine Oberflächenprojektion σ zum Flugzeug zOx. Die Projektion ist ein Dreieck AOC, das durch Geraden begrenzt ist oder , X= 0 und z= 0 . Wir berechnen:

Wir addieren die beiden resultierenden Integrale und erhalten schließlich dieses Flächenintegral:

.

Beispiel 6. Berechnen Sie Flächenintegrale zweiter Art

,

Wo σ - die äußere Oberfläche einer Pyramide, die durch eine Ebene gebildet wird und Koordinatenebenen.

Beispiel 3.3. Berechnen Sie die Arbeit eines Vektorfeldes

A = 2X 2 j ich – xy 2 J

vom Ursprung O zum Punkt A(1;1), wenn die Bewegung entlang erfolgt: A) Liniensegment; B) Bögen einer Parabel; V) gestrichelte Linie OBA, wobei B(1;0) (siehe Abb. 3.1).

Lösung . A) Die Geradengleichung OA hat die Form y=x. Lassen x=t, dann nimmt die Gleichung der Geraden in parametrischer Form die Form an:

x=t, y=t,

und beim Übergang von A nach B der Parameter Tändert sich von 0 auf 1. Dann ist die geleistete Arbeit gleich

B) Lassen x=t 2 , y=t, Dann

x=t 2 , y=t, 0£ T 1 £ .

.

V) Die Gleichung der Geraden (OB) lautet j=0 (0£ X 1 £); die Geradengleichung (BA) hat die Form X=1 (0 £ j 1 £). Dann

, .

Als Ergebnis erhalten wir,

.

Kommentar. Bei zweidimensionalen Feldern wird die Geradengleichung durch die Gleichung beschrieben j=j(X), und die Variable x variiert von A Vor B, dann wird das krummlinige Integral des 2. nach der Formel berechnet:

. (3.9)

Das vorherige Beispiel konnte mit dieser Formel gelöst werden, ohne den Parameter einzuführen T.

Beispiel 3.4. Integral berechnen

,

wobei L der Bogen der Parabel ist y=x 2 +1 von Punkt A(0;1) zu Punkt B(2;5).

Lösung . Machen wir eine Zeichnung (siehe Abb. 3.2). Aus der Parabelgleichung erhalten wir y"=2x. Da auf dem Bogen einer Parabel AB Variable Xändert sich von 0 auf 2, dann nimmt das krummlinige Integral gemäß Formel (3.9) die Form an

4. OBERFLÄCHENINTEGRALE

4.1. Oberflächenintegrale erster Art

Das Flächenintegral 1. Art ist eine Verallgemeinerung des Doppelintegrals und wird auf ähnliche Weise eingeführt. Betrachten Sie eine Oberfläche S, glatt oder stückweise glatt, und nehmen Sie an, dass die Funktion f( x,y,z) ist auf dieser Oberfläche definiert und begrenzt. Teilen wir diese Fläche in N beliebige Teile. Die Fläche jedes Grundstücks wird mit D bezeichnet s i. Auf jedem Abschnitt wählen wir einen Punkt mit Koordinaten ( x i ,y i ,z i) und berechnen Sie den Wert der Funktion an jedem dieser Punkte. Danach bilden wir die Integralsumme:

.

Wenn es eine Grenze ganzzahliger Summen gibt bei N®¥ (in diesem Fall max. D s i®0), d.h. Hängt eine solche Grenze weder von der Methode der Partitionierung noch von der Wahl der Mittelpunkte ab, dann heißt eine solche Grenze Oberflächenintegral erster Art :

. (4.1)

Wenn die Funktion f( x,y,z) ist an der Oberfläche kontinuierlich S, dann existiert Grenzwert (4.1).

Wenn die Integrandenfunktion f( x,y,z)º1, dann ist das Flächenintegral 1. Art gleich der Fläche S:

. (4.2)

Nehmen wir an, dass ein kartesisches Koordinatensystem eingeführt wird und eine beliebige Gerade parallel zur Achse verläuft Oz, kann die Oberfläche überqueren S nur an einer Stelle. Dann die Oberflächengleichung S kann in das Formular geschrieben werden

z = z(x,y)

und es wird eindeutig auf die Ebene projiziert xOy. Dadurch lässt sich das Flächenintegral 1. Art als Doppelintegral ausdrücken

. (4.3)

Beispiel 4.1. Integral berechnen

,

Wo S– Teil der konischen Oberfläche z 2 =X 2 +j 2,0 £ z 1 £.

Lösung. Wir haben

Anschließend wird das benötigte Integral in ein Doppelintegral umgewandelt

Wo S xy- Kreis X 2 +j 2 £1. Deshalb

.

4.2. Oberflächenintegrale zweiter Art

Es sei ein Vektorfeld in einer Region angegeben

A = ein x ich + ein y J + ein z k

und jede doppelseitige Oberfläche S. Unterteilen wir die Oberfläche auf irgendeine Weise in Elementarbereiche D S i. Auf jeder Seite wählen wir einen beliebigen Punkt P ich und bilden Sie die Integralsumme:

, (4.4)

Wo N (P ich) – Normalenvektor zu einer gegebenen Oberfläche an einem Punkt P ich. Gibt es unter D. eine Grenze für einen solchen Betrag? S i®0, dann heißt dieser Grenzwert Flächenintegral 2. Art (oder fließen Vektorfeld A durch die Oberfläche S) und wird durch das Symbol gekennzeichnet

oder ,

Wo D S =N ds.

Da der Einheitsnormalenvektor Richtungskosinus als Koordinaten hat N =(cosa, cosb, cosg). Das

Damit lässt sich die Berechnung von Flächenintegralen 2. Art auf die Berechnung von Flächenintegralen 1. Art reduzieren. Doch was Im Gegensatz zu Flächenintegralen 1. Art hängen Integrale 2. Art von der Wahl der Flächenseite ab. Der Übergang auf die andere Seite der Oberfläche ändert die Richtung der Flächennormalen und dementsprechend das Vorzeichen des Integrals.

Betrachten Sie das Integral

.

Die Oberflächengleichung soll die Form haben z=j( x,y) und die positive Seite dieser Oberfläche wird als diejenige betrachtet, deren Normalform mit der O-Achse verläuft z scharfe Ecke. Dann

cosg ds = dxdy.

Daher kann das betrachtete Integral in der Form geschrieben werden

.

Ersetzen z von j( x,y), kommen wir zum Doppelintegral

,

Wo S xy– Oberflächenprojektion S zum Flugzeug xOy.



Ähnliche Artikel