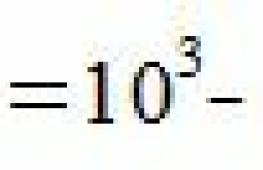Кто изобрел логарифм. История возникновения логарифма - реферат Сообщение на тему свойства логарифмов

26.12.2020

Логарифмы

История логарифмов

Название введено Непером, происходит от греческих слов logoz и ariumoz - оно означает буквально “числа отношений”. Логарифмы были изобретены Непером. Непер изобрел логарифмы не позднее 1594 года. Логарифмы с основанием a ввел учитель математики Спейдел. Слово основание заимствовано из теории о степенях и перенесено в теорию логарифмов Эйлером. Глагол “логарифмировать” появился в 19 веке у Коппе. Коши первый предложил ввести различные знаки для десятичных и натуральных логарифмов. Обозначения, близкие к современным ввел немецкий математик Прингсхейм в 1893 году. Именно он обозначал логарифм натурального числа через ln . Определение логарифма как показателя степени данного основания можно найти у Валлиса (1665 год), Бернулли (1694 год).

Определение логарифма

Логарифмом числа b>0 по основанию a>0, a ≠ 1 , называется показатель степени, в которую надо возвести число a, чтобы получить число b.

Логарифм числа b по основанию a обозначается: log a b

Основное логарифмическое тождество

Это равенство является просто другой формой определения логарифма. Его часто называют основным логарифмическим тождеством.

Пример

1. 3=log 2 8, так как 2³=8

2. ½=log 3 √3 , так как 3= √3

3. 3 log 3 1/5 =1/5

4. 2=log √5 5, так как (√5)²=5

Натуральный и десятичный логарифмы

Натуральным называется логарифм, основание которого равно e. Обозначается ln b, т.е.

Десятичным называется логарифм, основание которого равно 10. Обозначается lg b, т.е.

Основные свойства логарифмов

Пусть: a > 0, a ≠ 1. Тогда:

1. log a x*y=logax+logay (x>0, y>0)

2. log a y/x=logax−logay (x>0, y>0)

3. log a x p =p*logax (x>0)

4. log a p x=1/p*logax (x>0)

Пример

1) log 8 16+log 8 4= log 8 (16 4)= log 8 64= 2;

2) log 5 375– log 5 3= log 5 375/3=log 5 125= 3;

3) ½log 3 36+ log 3 2- log 3 √6- ½ log 3 8=log 3 √36+ log 3 2-(log 3 √6+log 3 √8) =log 3 12/4 √3=log 3 √3= ½.

Формы перехода от логарифма по одному основанию к логарифмы по другому основанию

1. log a b=log c b/log c a

2. log a b=1/log b a

Логарифмические уравнения

1) Уравнение содержащие переменную под знаком логарифма (log) называются логарифмическими. Простейшим примером логарифмического уравнения служит уравнение вида: log a x=b, где а>0 и а=1.

2) Решение логарифмического уравнения вида: log a f(x)=log a g(x) (1) основано на том, что оно равносильно уравнению вида f(x) = g(x) (2) при дополнительных условиях f(x)>0 и g(x)>0.

3) При переходе от уравнения (1) к уравнению (2) возможно появление посторонних корней поэтому для них выявления требуется проверка.

4) При решении логарифмических уравнений часто используется метод подстановки.

Вывод

Логарифм число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление - вычитанием, возведение в степень - умножением и извлечение корней - делением.

Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.

А теперь — собственно, определение логарифма:

Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a , чтобы получить число x .

Обозначение: log a x = b , где a — основание, x — аргумент, b — собственно, чему равен логарифм.

Например, 2 3 = 8 ⇒ log 2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log 2 64 = 6, поскольку 2 6 = 64.

Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log 2 2 = 1	log 2 4 = 2	log 2 8 = 3	log 2 16 = 4	log 2 32 = 5	log 2 64 = 6

К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log 2 5. Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2 < 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log 2 5, log 3 8, log 5 100.

Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:

Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень , в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.

С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:

Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!

Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.

Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log 2 0,5 = −1, т.к. 0,5 = 2 −1 .

Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.

Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:

Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
Решить относительно переменной b уравнение: x = a b ;
Полученное число b будет ответом.

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.

Посмотрим, как работает эта схема на конкретных примерах:

Задача. Вычислите логарифм: log 5 25

Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
Составим и решим уравнение:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
Получили ответ: 2.

Задача. Вычислите логарифм:

Задача. Вычислите логарифм: log 4 64

Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
Составим и решим уравнение:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
Получили ответ: 3.

Задача. Вычислите логарифм: log 16 1

Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
Составим и решим уравнение:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
Получили ответ: 0.

Задача. Вычислите логарифм: log 7 14

Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1 < 14 < 7 2 ;
Из предыдущего пункта следует, что логарифм не считается;
Ответ — без изменений: log 7 14.

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.

Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;

Заметим также, что сами простые числа всегда являются точными степенями самих себя.

Десятичный логарифм

Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.

Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x . Обозначение: lg x .

Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.

Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log 10 x

Все, что верно для обычных логарифмов, верно и для десятичных.

Натуральный логарифм

Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.

Натуральный логарифм от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x . Обозначение: ln x .

Многие спросят: что еще за число e ? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e = 2,718281828459...

Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = log e x

Таким образом, ln e = 1; ln e 2 = 2; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.

Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.

Открытие логарифмов опиралось на хорошо известные к концу 16 в. свойства прогрессий. Многие математики замечали, что умножению, делению, возведению в степень и извлечению корня в геометрической прогрессии соответствуют в арифметической прогрессии (в том же порядке) сложение, вычитание, умножение и деление. Настоящим триумфом стало открытие логарифмов как показателей степеней. Основные свойства логарифмов позволяют заменить умножение, возведение в степень и более простыми действиями сложения, вычитания, .

Логарифмы были изобретены независимо друг от друга Непером и Бюрги в начале 16 в. В 1614 г. Непер опубликован свое "Описание удивительной таблицы логарифмов", содержавшее определение логарифмов (и их свойства), которые теперь мы называем Неперовыми логарифмами, а в 1620 г. швейцарец Иост Бюрги (1552-1632) – опубликовал книгу "Таблицы арифметической и геометрической прогрессий, вместе с основательным наставлением, как их нужно понимать и с пользой применять во всяческих вычислениях". Однако таблицы Бюрги не получили значительного распространения.

Открытие логарифмов Непером, в первые же годы приобрело исключительно широкую известность. С логарифмами многие расчеты пошли в десятки раз быстрее и легче. Недаром великий французский математик Пьер Симон Лаплас говорил, что "изобретение логарифмов удлинило жизнь".

Термин "логарифм" (logarithmus) тоже принадлежит Неперу. Он возник из сочетания греческих слов: logos – "отношение" и arithmus – "число", т. е. означало число отношений. Однако ни у Непера, ни у Бюрги не было, строго говоря, основания логарифмов, поскольку логарифм единицы отличается от . Даже значительно позднее, когда уже перешли к десятичным и натуральным логарифмам, еще не было сформулировано определение логарифма как показателя степени данного основания.

Таблицы Непера, приспособленные к тригонометрическим вычислениям, были неудобны для действий с подобными числами. В 1615 г. Непер познакомился с Генри Бригсом (1561-1631) – профессором математики Грешем-колледжа, который тоже задумывался над тем, как усовершенствовать таблицы логарифмов. В ходе беседы с Бригсом Непер предложил составить таблицы логарифмов, приняв за логарифм единицы нуль, а за логарифм десяти - просто единицу, и таким образом устранить имевшиеся недостатки. Воплотить свои идеи в жизнь Непер не смог из-за пошатнувшегося здоровья, но он указал идею двух вычислительных приемов, развитых далее Бригсом.

В 1617 г. Бригс опубликовал первые результаты своих кропотливых вычислений – "Первую тысячу логарифмов". В этих таблицах были даны восьмизначные десятичные логарифмы чисел от 1 до 1000. Позднее (в 1624 г.), уже после того как он стал профессором в Оксфорде, Бригс выпустил "Логарифмическую арифметику". В книге содержались четырнадцатизначные логарифмы чисел от 1 до 20000 и от 90000 до 100000.

Сам термин "натуральный логарифм" в 1659 г. ввел Пьетро Менголи – итальянский математик, преподававший в Болонском университете, а знак Log был введен в 1624 г. Иоганном Кеплером (1571-1630), знаменитым немецким математиком, астрономом и оптиком, открывшим законы движения планет.

Следует отметить огромную работу, проделанную голландским математиком Андрианом Влакком. В 1628 г. он издал десятизначные таблицы логарифмов от 1 до 100000. Таблицы Влакка легли в основу большинства последующих таблиц, причем их авторы внесли много изменений в структуру логарифмических таблиц и поправок. В России таблицы логарифмов впервые были изданы в 1703 г. Л. Ф. Магницким.

За основание Бригговых логарифмов, как уже отмечалось, было взято число 10. В случае же Неперовых логарифмов сама константа (основание логарифмов) явно не определена. Первое известное использование этой константы, где она обозначалась буквой встречается в письмах Готфрида Лейбница к Кристиану Гюйгенсу в 1690 и 1691 гг. Букву е начал использовать Леонард Эйлер в 1727 г., а первой публикацией с использованием этой буквы была его работа "Механика, или Наука о движении, наложенная аналитически" (1736). Соответственно, е иногда называют числом Эйлера. В 1874 г. французский математик Ш. Эрмит доказал, что основание натуральных логарифмов е трансцендентно (как ). Величина е = 2,718 281 828 459 045 235 360 287 471 352 662 49.

Число е можно запомнить по следующему : два и семь, далее два раза год рождения Льва Толстого (1828), а затем углы равнобедренного прямоугольного треугольника (45. 90 и 45 градусов). А вот еще один оригинальный способ запоминания: предлагается запомнить число е с точностью до трех знаков после запятой через "число дьявола": нужно разделить 666 на число, составленное из цифр 6 - 4, 6 - 2, 6 - 1 (три шестерки, из которых в обратном порядке удаляются три первые степени двойки): 666/245 = 2,718.

Что такое логарифм?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")

Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно - уравнения с логарифмами.

Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 - 20 минут вы:

1. Поймете, что такое логарифм .

2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.

3. Научитесь вычислять простые логарифмы.

Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень...

Чувствую, сомневаетесь вы... Ну ладно, засекайте время! Поехали!

Для начала решите в уме вот такое уравнение:

Если Вам нравится этот сайт...

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)

можно познакомиться с функциями и производными.

(от греческого λόγος - «слово», «отношение» и ἀριθμός - «число») числа b по основанию a (log α b ) называется такое число c , и b = a c , то есть записи log α b =c и b=a c эквивалентны. Логарифм имеет смысл, если a > 0, а ≠ 1, b > 0.

Говоря другими словами логарифм числа b по основанию а формулируется как показатель степени , в которую надо возвести число a , чтобы получить число b (логарифм существует только у положительных чисел).

Из данной формулировки вытекает, что вычисление x= log α b , равнозначно решению уравнения a x =b.

Например:

log 2 8 = 3 потому, что 8=2 3 .

Выделим, что указанная формулировка логарифма дает возможность сразу определить значение логарифма , когда число под знаком логарифма выступает некоторой степенью основания. И в правду, формулировка логарифма дает возможность обосновать, что если b=a с , то логарифм числа b по основанию a равен с . Также ясно, что тема логарифмирования тесно взаимосвязана с темой степени числа .

Вычисление логарифма именуют логарифмированием . Логарифмирование - это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей трансформируется в суммы членов.

Потенцирование - это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов трансформируются в произведение сомножителей.

Достаточно часто используются вещественные логарифмы с основаниями 2 (двоичный), е число Эйлера e ≈ 2,718 (натуральный логарифм) и 10 (десятичный).

На данном этапе целесообразно рассмотреть образцы логарифмов log 7 2, ln√ 5, lg0.0001.

А записи lg(-3), log -3 3.2, log -1 -4.3 не имеют смысла, так как в первой из них под знаком логарифма помещено отрицательное число , во второй - отрицательное число в основании, а в третьей - и отрицательное число под знаком логарифма и единица в основании.

Условия определения логарифма.

Стоит отдельно рассмотреть условия a > 0, a ≠ 1, b > 0.при которых дается определение логарифма . Рассмотрим, почему взяты эти ограничения. В это нам поможет равенство вида x = log α b , называемое основным логарифмическим тождеством , которое напрямую следует из данного выше определения логарифма.

Возьмем условие a≠1 . Поскольку единица в любой степени равна единице, то равенство x=log α b может существовать лишь при b=1 , но при этом log 1 1 будет любым действительным числом . Для исключения этой неоднозначности и берется a≠1 .

Докажем необходимость условия a>0 . При a=0 по формулировке логарифма может существовать только при b=0 . И соответственно тогда log 0 0 может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Исключить эту неоднозначность дает условие a≠0 . А при a<0 нам бы пришлось отвергнуть разбор рациональных и иррациональных значений логарифма, поскольку степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Именно по этой причине и оговорено условие a>0 .

И последнее условие b>0 вытекает из неравенства a>0 , поскольку x=log α b , а значение степени с положительным основанием a всегда положительно.

Особенности логарифмов.

Логарифмы характеризуются отличительными особенностями , которые обусловили их повсеместное употребление для значительного облегчения кропотливых расчетов. При переходе «в мир логарифмов» умножение трансформируется на значительно более легкое сложение, деление — на вычитание, а возведение в степень и извлечение корня трансформируются соответствующе в умножение и деление на показатель степени.

Формулировку логарифмов и таблицу их значений (для тригонометрических функций) впервые издал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.