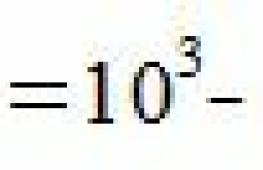Из записи a = b q следует, что b – делитель a и что a кратно b. Делители и кратные числа

«Десятичная запись числа» - Какую часть метра составляет 1 дм? Решите уравнение Какую часть отрезок CD составляет от отрезка АВ. Пашиева Любовь Николаевна учитель математики I категории. Десятичная запись дробных чисел. Десятичные дроби. Джон Непер. Среднеазиатский город Самарканд в XV веке был богатым культурным центром. Правила десятичной записи дробных чисел.

«Запись систем счисления» - Непозиционные системы счисления. А как человек записывал числа раньше? Если число 56 записано в десятичной системе счисления, то записывают так: Вспомним понятие степени числа: История чисел и системы счисления. Натуральный ряд чисел в позиционной системе счисления. Развернутая запись числа. Понятие «системы счисления».

«Запись информации на диск» - Запись с аудиодисков воспроизводится с помощью оптических (лазерных) проигрывателей. Производятся такие диски путем штамповки и имеют серебристый цвет. Лазерные дисководы. Существуют CD-R и DVD-R-диски (R - recordable, запи­сываемый), которые имеют золотистый цвет. Оптический принцип записи. Длительность звуковой программы достигает одного часа.

«Запись чисел в системах счисления» - В алфавитной славянской системе счисления в качестве “цифр” использовалось 27 букв кириллицы. Более совершенными непозиционными системами счисления были алфавитные системы. Алфавитные системы. В такой форме представляется содержимое любого файла. Древнеегипетская десятичная непозиционная система. Римская система счисления.

«Десятичная запись дробных чисел» - Записать числитель дробной части. «Что есть арифметика? Десятичная запись дробных чисел. Симон Стевин (1548 – 1620). Уравнять, если необходимо, число цифр после запятой. Л.Ф. Магницкий (1669-1739). М.В. Абанина. Поставить запятую, отделяющую целую часть от дробной.

«Делители и кратные» - ТЕМА: Делители и кратные. Совершенные числа. В ы ч и с л и т ь устно. Выберите из чисел: Три в ладошки, три хлопка, Головою три кивка. Раз согнуться – разогнуться, Два нагнуться – подтянуться. Физкульминутка. Каких делителей числа 24 нет среди данных чисел? Запишите в тетрадях число и тему урока: «Делители и кратные».

Определение 1. Пусть число a 1) есть произведение двух чисел b и q так, что a=bq. Тогда a называется кратным b .

1) В данной статье под словом число будем понимать целое число.

Можно сказать также a делится на b, или b есть делитель a , или b делит a , или b входит множителем в a .

Из определения 1 вытекают следующие утверждения:

Утверждение 1. Если a -кратное b , b -кратное c , то a кратное c .

Действительно. Так как

где m и n какие то числа, то

Следовательно a делится на c.

Если в ряду чисел, каждое делится на следующее за ним, то каждое число есть кратное всех последующих чисел.

Утверждение 2. Если числа a и b - кратные числа c , то их сумма и разность также кратные числа c .

Действительно. Так как

a+b=mc+nc=(m+n)c,

a−b=mc−nc=(m−n)c.

Следовательно a+b делится на c и a−b делится на c .

Признаки делимости

Выведем общую формулу для определения признака делимости чисел на некоторое натуральное число m , которое называется признаком делимости Паскаля.

Найдем остатки деления на m следующей последовательностью. Пусть остаток от деления 10 на m будет r 1 , 10·r 1 на m будет r 2 , и т.д. Тогда можно записать:

Докажем, что остаток деления числа A на m равна остатку деления числа

(3)

Как известно, если два числа при делении на какое то число m дают одинаковый остаток, то из разность делится на m без остатка.

Рассмотрим разность A−A"

(6)

(7)

Каждый член правой части (5) делится на m следовательно левая часть уравнения также делится на m . Рассуждая аналогично, получим - правая часть (6) делится на m , следовательно левая часть (6) также делится на m , правая часть (7) делится на m , следовательно левая часть (7) также делится на m . Получили, что правая часть уравнения (4) делится на m . Следовательно A и A" имеют одинаковый остаток при делении на m . В этом случае говорят, что A и A" равноостаточные или сравнимыми по модулю m .

Таким образом, если A" делится на m m ) , то A также делится на m (имеет нулевой остаток от деления на m ). Мы показали что для определения делимости A можно определить делимость более простого числа A" .

Исходя из выражения (3), можно получить признаки делимости для конкретных чисел.

Признаки делимости чисел 2, 3, 4, 5, 6, 7, 8, 9, 10

Признак делимости на 2.

Следуя процедуре (1) для m=2 , получим:

Все остатки от деления на 2 равняются нулю. Тогда, из уравнения (3) имеем

Все остатки от деления на 3 равняются 1. Тогда, из уравнения (3) имеем

Все остатки от деления на 4 кроме первого равняются 0. Тогда, из уравнения (3) имеем

Все остатки равны нулю. Тогда, из уравнения (3) имеем

Все остатки равны 4. Тогда, из уравнения (3) имеем

Следовательно число делится на 6 тогда и только тогда, когда учетверённое число десятков, сложенное с числом единиц, делится на 6. То есть из числа отбрасываем правую цифру, далее суммируем полученное число с 4 и добавляем отброшенное число. Если данное число делится на 6, то исходное число делится на 6.

Пример. 2742 делится на 6, т.к. 274*4+2=1098, 1098=109*4+8=444, 444=44*4+4=180 делится на 6.

Более простой признак делимости. Число делится на 6, если оно делится на 2 и на 3 (т.е. если оно четное число и если сумма цифр делится на 3). Число 2742 делится на 6, т.к. число четное и 2+7+4+2=15 делится на 3.

Признак делимости на 7.

Следуя процедуре (1) для m=7 , получим:

Все остатки разные и повторяются через 7 шагов. Тогда, из уравнения (3) имеем

Все остатки все остатки нулевые, кроме первых двух. Тогда, из уравнения (3) имеем

Все остатки от деления на 9 равняются 1. Тогда, из уравнения (3) имеем

Все остатки от деления на 10 равняются 0. Тогда, из уравнения (3) имеем

Следовательно число делится на 10 тогда и только тогда, когда последняя цифра делится на 10 (то есть последняя цифра нулевая).

В этой статье мы обсудим делители и кратные . Здесь мы дадим определения делителя и кратного числа. Эти определения нам позволят привести примеры делителей и кратных различных целых чисел. Отдельно рассмотрим делители единицы и минус единицы, а также поговорим о делителях и кратных нуля.

Навигация по странице.

Делители числа – определение, примеры

Сначала дадим определение делителя целого числа.

Определение.

Делителем целого числа a называется целое число b , на которое a делится нацело.

Натуральное число 1 имеет единственный положительный делитель – это число 1 . Этот факт отличает единицу от других натуральных чисел, так как натуральные числа, отличные от единицы, имеют не менее двух делителей, а именно себя самого и 1 . В зависимости от отсутствия или наличия делителей, отличных от самого натурального числа и от единицы, различают простые и составные числа .

Единица является наименьшим положительным делителем натурального числа a , отличного от 1 , а само число a является наибольшим положительным делителем (о наибольшем и наименьшем числе мы говорили в разделе ). То есть, для любого натурального числа a любой его положительный делитель b удовлетворяет условию .

Кратные числа – определение, примеры

Дадим определение кратного .

Определение.

Кратное целого числа b – это целое число a , которое делится на b нацело.

Иными словами, кратное целого числа b – это такое целое число a , которое может быть представлено в форме a=b·q , где q – некоторое целое число.

Если a является кратным целого числа b , то говорят, что a кратно b . При этом применяют обозначение ab .

Определение кратного и делимого явно указывает на существующую между ними связь. Действительно, по определению если a – кратное числа b , то b – делитель числа a , и наоборот, если b – делитель числа a , то a – кратное числа b .

Приведем примеры кратных . Например, целое число −12 есть кратное числа 3 , так как −12=3·(−4) . Другими кратными числа 3 являются целые числа 0 , 3 , −3 , 6 , −6 , 9 , −9 и так далее. А вот число 7 не является кратным целого числа 3 , так как 7 не делится на 3 без остатка, то есть, не существует такого целого числа q , чтобы выполнялось равенство 7=3·q .

Из определения кратного числа понятно, что нуль является кратным любого целого числа b , в том числе и нуля. Равенство 0=b·0 в этом случае выглядит очень доказательно.

Отметим, что существует бесконечно много кратных любого целого числа b , так как целых чисел бесконечно много, и любое целое число, равное произведению b·q , где q – произвольное целое число, является кратным числа b .

Наименьшим положительным кратным данного положительного числа a является само это число a . Здесь же стоит обратить внимание на то, что наименьшее положительное кратное не стоит путать с наименьшим общим кратным (НОК) нескольких чисел.

Дальше мы можем рассматривать лишь натуральные кратные целых положительных чисел. Это мы можем делать в силу тех же причин, которые были упомянуты в первом пункте этой статьи, при этом общность изложения не будет нарушена.

Список литературы.

• Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
• Виноградов И.М. Основы теории чисел.
• Михелович Ш.Х. Теория чисел.
• Куликов Л.Я. и др. Сборник задач по алгебре и теории чисел: Учебное пособие для студентов физ.-мат. специальностей педагогических институтов.

Тема «Кратные числа» изучается в 5 классе общеобразовательной школы. Ее целью является совершенствование письменных и устных навыков математических вычислений. На этом уроке вводятся новые понятия - «кратные числа» и «делители», отрабатывается техника нахождения делителей и кратных натурального числа, умение находить НОК различными способами.

Эта тема является очень важной. Знания по ней можно применить при решении примеров с дробями. Для этого нужно найти общий знаменатель путем расчета наименьшего общего кратного (НОК).

Кратным А считается целое число, которое делится на А без остатка.

Каждое натуральное число имеет бесконечное количество кратных ему чисел. Наименьшим считается оно само. Кратное не может быть меньше самого числа.

Нужно доказать, что число 125 кратно числу 5. Для этого нужно первое число разделить на второе. Если 125 делится на 5 без остатка, то ответ положительный.

Данный способ применим для небольших чисел.

При расчёте НОК встречаются особые случаи.

1. Если необходимо найти общее кратное для 2-х чисел (например, 80 и 20), где одно из них (80) делится без остатка на другое (20), то это число (80) и есть наименьшее кратное этих двух чисел.

НОК (80, 20) = 80.

2. Если два не имеют общего делителя, то можно сказать, что их НОК - это произведение этих двух чисел.

НОК (6, 7) = 42.

Рассмотрим последний пример. 6 и 7 по отношению к 42 являются делителями. Они делят кратное число без остатка.

В этом примере 6 и 7 являются парными делителями. Их произведение равно самому кратному числу (42).

Число называется простым, если делится только само на себя или на 1 (3:1=3; 3:3=1). Остальные называются составными.

В другом примере нужно определить, является ли 9 делителем по отношению к 42.

42:9=4 (остаток 6)

Ответ: 9 не является делителем числа 42, потому что в ответе есть остаток.

Делитель отличается от кратного тем, что делитель - это то число, на которое делят натуральные числа, а кратное само делится на это число.

Наибольший общий делитель чисел a и b , умноженный на их наименьшее кратное, даст произведение самих чисел a и b .

А именно: НОД (а, b) х НОК (а, b) = а х b.

Общие кратные числа для более сложных чисел находят следующим способом.

Например, найти НОК для 168, 180, 3024.

Эти числа раскладываем на простые множители, записываем в виде произведения степеней:

168=2³х3¹х7¹

2⁴х3³х5¹х7¹=15120

НОК (168, 180, 3024) = 15120.