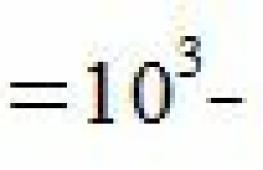Spazi lineari. Sottospazi
Quando abbiamo esaminato i concetti di un vettore n-dimensionale e introdotto le operazioni sui vettori, abbiamo scoperto che l'insieme di tutti i vettori n-dimensionali genera uno spazio lineare. In questo articolo parleremo dei concetti correlati più importanti: la dimensione e la base di uno spazio vettoriale. Considereremo anche il teorema sull'espansione di un vettore arbitrario in una base e la connessione tra varie basi dello spazio n-dimensionale. Esaminiamo in dettaglio le soluzioni di esempi tipici.
Navigazione della pagina.
Il concetto di dimensione dello spazio vettoriale e di base.
I concetti di dimensione e base di uno spazio vettoriale sono direttamente correlati al concetto di sistema di vettori linearmente indipendenti, quindi, se necessario, ti consigliamo di fare riferimento all'articolo dipendenza lineare di un sistema di vettori, proprietà di dipendenza lineare e indipendenza .
Definizione.
Dimensione dello spazio vettorialeè un numero pari al numero massimo di vettori linearmente indipendenti in questo spazio.
Definizione.
Base dello spazio vettorialeè un insieme ordinato di vettori linearmente indipendenti di questo spazio, il cui numero è uguale alla dimensione dello spazio.
Facciamo qualche ragionamento basato su queste definizioni.
Considera lo spazio dei vettori n-dimensionali.
Mostriamo che la dimensione di questo spazio è n.
Prendiamo un sistema di n vettori unitari della forma
Prendiamo questi vettori come righe della matrice A. In questo caso, la matrice A sarà una matrice identità di dimensione n per n. Il rango di questa matrice è n (vedi articolo se necessario). Pertanto, il sistema di vettori 
è linearmente indipendente e non è possibile aggiungere un singolo vettore a questo sistema senza violarne l'indipendenza lineare. Poiché il numero di vettori nel sistema è uguale a n, quindi la dimensione dello spazio dei vettori n-dimensionali è n, e i vettori unitari sono la base di questo spazio.
Dall'ultima affermazione e dalla definizione della base possiamo concludere questo qualsiasi sistema di vettori n-dimensionali, il cui numero di vettori è inferiore a n, non è una base.
Ora scambiamo il primo e il secondo vettore del sistema . È facile dimostrare che il sistema di vettori risultante 
è anche una base di uno spazio vettoriale n-dimensionale. Creiamo una matrice prendendo i vettori di questo sistema come sue righe. Questa matrice può essere ottenuta dalla matrice identità scambiando la prima e la seconda riga, quindi il suo rango sarà n. Quindi un sistema di n vettori è linearmente indipendente ed è la base di uno spazio vettoriale n-dimensionale.
Se riorganizziamo altri vettori del sistema , allora otteniamo un'altra base.
Se prendiamo un sistema linearmente indipendente di vettori non unitari, allora è anche la base di uno spazio vettoriale n-dimensionale.
Così, uno spazio vettoriale di dimensione n ha tante basi quanti sono i sistemi linearmente indipendenti di n vettori n -dimensionali.
Se parliamo di uno spazio vettoriale bidimensionale (cioè di un piano), allora la sua base sono due vettori non collineari qualsiasi. La base dello spazio tridimensionale sono tre vettori qualsiasi non complanari.
Diamo un'occhiata ad alcuni esempi.
Esempio.
I vettori sono la base dello spazio vettoriale tridimensionale?
Soluzione.
Esaminiamo questo sistema di vettori per la dipendenza lineare. Per fare ciò, creiamo una matrice le cui righe saranno le coordinate dei vettori e troviamo il suo rango: 
Pertanto, i vettori a, b e c sono linearmente indipendenti e il loro numero è uguale alla dimensione dello spazio vettoriale, quindi sono la base di questo spazio.
Risposta:
Sì.
Esempio.
Un sistema di vettori può essere la base di uno spazio vettoriale?
Soluzione.
Questo sistema di vettori è linearmente dipendente, poiché il numero massimo di vettori tridimensionali linearmente indipendenti è tre. Di conseguenza, questo sistema di vettori non può essere la base di uno spazio vettoriale tridimensionale (sebbene un sottosistema del sistema di vettori originale sia una base).
Risposta:
No non può.
Esempio.
Assicurati che i vettori 
può essere la base di uno spazio vettoriale quadridimensionale.
Soluzione.
Creiamo una matrice prendendo i vettori originali come righe: 
Cerchiamo: 
Pertanto, il sistema di vettori a, b, c, d è linearmente indipendente e il loro numero è uguale alla dimensione dello spazio vettoriale, quindi a, b, c, d sono la sua base.
Risposta:
I vettori originali sono infatti la base dello spazio quadridimensionale.
Esempio.
I vettori costituiscono la base di uno spazio vettoriale di dimensione 4?
Soluzione.
Anche se il sistema di vettori originale è linearmente indipendente, il numero di vettori in esso contenuti non è sufficiente per costituire la base di uno spazio quadridimensionale (la base di tale spazio è composta da 4 vettori).
Risposta:
No, non è così.
Scomposizione di un vettore secondo le basi dello spazio vettoriale.
Consideriamo i vettori arbitrari sono la base di uno spazio vettoriale n-dimensionale. Se aggiungiamo ad essi un vettore n-dimensionale x, il sistema di vettori risultante sarà linearmente dipendente. Dalle proprietà della dipendenza lineare sappiamo che almeno un vettore di un sistema linearmente dipendente si esprime linearmente attraverso gli altri. In altre parole, almeno uno dei vettori di un sistema linearmente dipendente viene espanso nei restanti vettori.
Questo ci porta ad un teorema molto importante.
Teorema.
Qualsiasi vettore di uno spazio vettoriale n-dimensionale può essere scomposto in modo univoco in una base.
Prova.
Permettere - base dello spazio vettoriale n-dimensionale. Aggiungiamo un vettore n-dimensionale x a questi vettori. Quindi il sistema di vettori risultante sarà linearmente dipendente e il vettore x potrà essere espresso linearmente in termini di vettori : , dove sono alcuni numeri. In questo modo abbiamo ottenuto l'espansione del vettore x rispetto alla base. Resta da dimostrare che questa scomposizione è unica.
Supponiamo che ci sia un'altra scomposizione, dove 
- alcuni numeri. Sottraiamo dai lati sinistro e destro dell'ultima uguaglianza rispettivamente i lati sinistro e destro dell'uguaglianza:
Poiché il sistema dei vettori di base è linearmente indipendente, allora per la definizione di indipendenza lineare di un sistema di vettori, l'uguaglianza risultante è possibile solo quando tutti i coefficienti sono uguali a zero. Pertanto, , che dimostra l'unicità della scomposizione vettoriale rispetto alla base.
Definizione.
I coefficienti sono chiamati coordinate del vettore x nella base .
Dopo aver acquisito familiarità con il teorema sulla scomposizione di un vettore in una base, iniziamo a comprendere l'essenza dell'espressione “ci viene dato un vettore n-dimensionale 
" Questa espressione significa che stiamo considerando un vettore di spazio vettoriale x n -dimensionale, le cui coordinate sono specificate in qualche base. Allo stesso tempo, comprendiamo che lo stesso vettore x in un'altra base dello spazio vettoriale n-dimensionale avrà coordinate diverse da .
Consideriamo il seguente problema.
Sia dato un sistema di n vettori linearmente indipendenti in una base di spazio vettoriale n-dimensionale 
e vettore . Poi i vettori sono anche la base di questo spazio vettoriale.
Dobbiamo trovare le coordinate del vettore x nella base . Indichiamo queste coordinate come .
Vettore x in base ha un'idea. Scriviamo questa uguaglianza in forma di coordinate:
Questa uguaglianza equivale a un sistema di n equazioni algebriche lineari con n variabili incognite :
La matrice principale di questo sistema ha la forma 
Indichiamolo con la lettera A. Le colonne della matrice A rappresentano i vettori di un sistema di vettori linearmente indipendenti , quindi il rango di questa matrice è n, quindi il suo determinante è diverso da zero. Questo fatto indica che il sistema di equazioni ha una soluzione unica che può essere trovata con qualsiasi metodo, ad esempio, o.
In questo modo verranno trovate le coordinate richieste vettore x nella base .
Diamo un'occhiata alla teoria usando esempi.
Esempio.
In alcune basi dello spazio vettoriale tridimensionale, i vettori 
Assicurati che anche il sistema di vettori sia una base di questo spazio e trova le coordinate del vettore x in questa base.
Soluzione.
Affinché un sistema di vettori sia la base di uno spazio vettoriale tridimensionale, deve essere linearmente indipendente. Scopriamolo determinando il rango della matrice A, le cui righe sono vettori. Troviamo il rango utilizzando il metodo gaussiano 
quindi Rank(A) = 3, che mostra l'indipendenza lineare del sistema di vettori.
Quindi, i vettori sono la base. Sia il vettore x ad avere coordinate in questa base. Quindi, come abbiamo mostrato sopra, la relazione tra le coordinate di questo vettore è data dal sistema di equazioni 
Sostituendo in essa i valori noti dalla condizione, otteniamo 
Risolviamolo utilizzando il metodo di Cramer: 
Pertanto, il vettore x nella base ha coordinate 
.
Risposta:
Esempio.
In qualche modo 
di uno spazio vettoriale quadridimensionale, è dato un sistema di vettori linearmente indipendenti 
È risaputo che 
. Trova le coordinate del vettore x nella base .
Soluzione.
Poiché il sistema di vettori 
linearmente indipendente dalla condizione, allora è una base dello spazio quadridimensionale. Poi l'uguaglianza significa che il vettore x nella base ha delle coordinate. Indichiamo le coordinate del vettore x nella base Come .
Sistema di equazioni che definiscono la relazione tra le coordinate del vettore x in basi E sembra 
Sostituiamo i valori noti e troviamo le coordinate richieste: 
Risposta:
.
Comunicazione tra basi.
Siano dati due sistemi di vettori linearmente indipendenti in una base di uno spazio vettoriale n-dimensionale 
E
cioè sono anche le basi di questo spazio.
Se 
- coordinate del vettore nella base , quindi la connessione delle coordinate 
E è dato da un sistema di equazioni lineari (ne abbiamo parlato nel paragrafo precedente): 
, che in forma matriciale può essere scritto come 
Allo stesso modo per un vettore possiamo scrivere 
Le precedenti uguaglianze della matrice possono essere combinate in una sola, che definisce essenzialmente la relazione tra i vettori di due basi diverse 
Allo stesso modo, possiamo esprimere tutti i vettori di base tramite base 
:
Definizione.
Matrice 
chiamato matrice di transizione dalla base alla base , allora l'uguaglianza è vera 
Moltiplicando entrambi i lati di questa uguaglianza da destra per
noi abbiamo 
Troviamo la matrice di transizione, ma non ci soffermeremo in dettaglio sulla ricerca della matrice inversa e sulla moltiplicazione delle matrici (vedi articoli e se necessario): 
Resta da scoprire la relazione tra le coordinate del vettore x nelle basi date.
Sia allora il vettore x ad avere coordinate nella base 
e nella base il vettore x ha coordinate , quindi 
Poiché i lati sinistri delle ultime due uguaglianze sono uguali, possiamo uguagliare i lati destri: 
Se moltiplichiamo entrambi i membri a destra per
allora otteniamo 
Dall'altro lato 
(trova tu stesso la matrice inversa).
Le ultime due uguaglianze ci danno la relazione richiesta tra le coordinate del vettore x nelle basi e .
Risposta:
La matrice di transizione da base a base ha la forma 
;
coordinate del vettore x in basi e sono legate dalle relazioni 
O .
Abbiamo esaminato i concetti di dimensione e base di uno spazio vettoriale, imparato a scomporre un vettore in una base e scoperto la connessione tra diverse basi dello spazio vettoriale n-dimensionale attraverso la matrice di transizione.
Lo spazio lineare si chiama V n-dimensionale, se in esso esiste un sistema di n vettori linearmente indipendenti e qualsiasi sistema di più vettori è linearmente dipendente. Viene chiamato il numero n dimensione (numero di dimensioni) spazio lineare V ed è indicato \nomeoperatore(dim)V. In altre parole, la dimensione di uno spazio è il numero massimo di vettori linearmente indipendenti di questo spazio. Se tale numero esiste, lo spazio è detto a dimensione finita. Se per qualsiasi numero naturale n nello spazio V esiste un sistema costituito da n vettori linearmente indipendenti, allora tale spazio è chiamato infinito (scrivi: \nomeoperatore(dim)V=\infty). Nel seguito, salvo diversa indicazione, verranno considerati spazi a dimensione finita.
Base Uno spazio lineare n-dimensionale è una raccolta ordinata di n vettori linearmente indipendenti ( vettori di base).
Teorema 8.1 sullo sviluppo di un vettore in termini di base. Se è la base di uno spazio lineare n-dimensionale V, allora qualsiasi vettore \mathbf(v)\in V può essere rappresentato come una combinazione lineare di vettori di base:
\mathbf(v)=\mathbf(v)_1\cdot \mathbf(e)_1+\mathbf(v)_2\cdot \mathbf(e)_2+\ldots+\mathbf(v)_n\cdot \mathbf(e)_n
e, inoltre, nell'unico modo, cioè probabilità \mathbf(v)_1, \mathbf(v)_2,\ldots, \mathbf(v)_n sono determinati in modo inequivocabile. In altre parole, qualsiasi vettore dello spazio può essere espanso in una base e, inoltre, in un modo unico.
Infatti la dimensione dello spazio V è pari a n. Sistema vettoriale \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n linearmente indipendente (questa è una base). Dopo aver aggiunto alla base un qualsiasi vettore \mathbf(v), otteniamo un sistema linearmente dipendente \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n, \mathbf(v)(poiché questo sistema è costituito da (n+1) vettori di spazio n-dimensionale). Utilizzando la proprietà di 7 vettori linearmente dipendenti e linearmente indipendenti, otteniamo la conclusione del teorema.
Corollario 1. Se \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_nè la base dello spazio V, quindi V=\nomeoperatore(Lin) (\mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_n), cioè. uno spazio lineare è l'estensione lineare dei vettori di base.
In effetti, per dimostrare l'uguaglianza V=\nomeoperatore(Lin) (\mathbf(e)_1,\mathbf(e)_2, \ldots, \mathbf(e)_n) due insiemi, è sufficiente mostrare che le inclusioni V\subset \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_n) e vengono eseguiti simultaneamente. Infatti, da un lato, qualsiasi combinazione lineare di vettori in uno spazio lineare appartiene allo spazio lineare stesso, cioè \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n)\subset V. D'altra parte, secondo il Teorema 8.1, qualsiasi vettore dello spazio può essere rappresentato come una combinazione lineare di vettori di base, cioè V\subset \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n). Ciò implica l’uguaglianza degli insiemi considerati.
Corollario 2. Se \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- un sistema linearmente indipendente di vettori dello spazio lineare V e un qualsiasi vettore \mathbf(v)\in V può essere rappresentato come una combinazione lineare (8.4): \mathbf(v)=v_1\mathbf(e)_1+ v_2\mathbf(e)_2+\ldots+v_n\mathbf(e)_n, allora lo spazio V ha dimensione n, e il sistema \mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_nè la sua base.
Infatti nello spazio V esiste un sistema di n vettori linearmente indipendenti, e qualsiasi sistema \mathbf(u)_1,\mathbf(u)_2,\ldots,\mathbf(u)_n di un numero maggiore di vettori (k>n) è linearmente dipendente, poiché ogni vettore di questo sistema è espresso linearmente in termini di vettori \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n. Significa, \nomeoperatore(dim) V=n E \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- base V.
Teorema 8.2 sull'addizione di un sistema di vettori ad una base. Qualsiasi sistema linearmente indipendente di k vettori di spazio lineare n-dimensionale (1\leqslant k Sia infatti un sistema di vettori linearmente indipendenti nello spazio n-dimensionale V~(1\leqinclinazione k Note 8.4 1. La base di uno spazio lineare è determinata in modo ambiguo. Ad esempio, se \mathbf(e)_1,\mathbf(e)_2, \ldots, \mathbf(e)_nè la base dello spazio V, quindi il sistema di vettori \lambda \mathbf(e)_1,\lambda \mathbf(e)_2,\ldots,\lambda \mathbf(e)_n poiché ogni \lambda\ne0 è anche una base di V . Il numero di vettori di base in basi diverse dello stesso spazio a dimensione finita è, ovviamente, lo stesso, poiché questo numero è uguale alla dimensione dello spazio. 2. In alcuni spazi, spesso riscontrati nelle applicazioni, una delle basi possibili, la più conveniente dal punto di vista pratico, si chiama standard. 3. Il Teorema 8.1 ci permette di dire che una base è un sistema completo di elementi di uno spazio lineare, nel senso che qualsiasi vettore dello spazio è espresso linearmente in termini di vettori di base. 4. Se l'insieme \mathbb(L) è uno span lineare \nomeoperatore(Lin)(\mathbf(v)_1,\mathbf(v)_2,\ldots,\mathbf(v)_k), quindi i vettori \mathbf(v)_1,\mathbf(v)_2,\ldots,\mathbf(v)_k sono detti generatori dell'insieme \mathbb(L) . Corollario 1 del Teorema 8.1 dovuto all'uguaglianza V=\nomeoperatore(Lin) (\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n) ci permette di dire che la base è sistema generatore minimo spazio lineare V, poiché è impossibile ridurre il numero di generatori (rimuovere almeno un vettore dall'insieme \mathbf(e)_1, \mathbf(e)_2,\ldots,\mathbf(e)_n) senza violare l'uguaglianza V=\nomeoperatore(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n). 5. Il Teorema 8.2 ci permette di dire che la base è massimo sistema di vettori linearmente indipendenti spazio lineare, poiché la base è un sistema di vettori linearmente indipendenti e non può essere integrato con alcun vettore senza perdere l'indipendenza lineare. 6. Il Corollario 2 del Teorema 8.1 è conveniente da utilizzare per trovare base e dimensione di uno spazio lineare. In alcuni libri di testo si intende definire la base, vale a dire: sistema linearmente indipendente \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n di vettori di uno spazio lineare si dice base se qualsiasi vettore dello spazio è espresso linearmente in termini di vettori \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n. Il numero di vettori di base determina la dimensione dello spazio. Naturalmente, queste definizioni sono equivalenti a quelle fornite sopra. Indichiamo la dimensione e la base per gli esempi di spazi lineari discussi sopra. 1. Lo spazio lineare zero \(\mathbf(o)\) non contiene vettori linearmente indipendenti. Pertanto, si assume che la dimensione di questo spazio sia zero: \dim\(\mathbf(o)\)=0. Questo spazio non ha basi. 2. Gli spazi V_1,\,V_2,\,V_3 hanno dimensione 1, 2, 3, rispettivamente. Infatti, qualsiasi vettore diverso da zero dello spazio V_1 forma un sistema linearmente indipendente (vedi punto 1 delle Osservazioni 8.2), e due vettori qualsiasi diversi da zero dello spazio V_1 sono collineari, cioè linearmente dipendente (vedi esempio 8.1). Di conseguenza, \dim(V_1)=1, e la base dello spazio V_1 è un qualsiasi vettore diverso da zero. Allo stesso modo, è dimostrato che \dim(V_2)=2 e \dim(V_3)=3 . La base dello spazio V_2 sono due vettori non collineari qualsiasi presi in un certo ordine (uno di essi è considerato il primo vettore base, l'altro il secondo). La base dello spazio V_3 sono tre vettori qualsiasi non complanari (che non giacciono sullo stesso piano o su piani paralleli), presi in un certo ordine. La base standard in V_1 è il vettore unitario \vec(i) sulla linea. La base standard in V_2 è la base \vec(i),\,\vec(j), costituito da due vettori unitari del piano reciprocamente perpendicolari. Come base è considerata la base standard nello spazio V_3 \vec(i),\,\vec(j),\,\vec(k), composto da tre vettori unitari, perpendicolari a due a due, che formano una terna retta. 3. Lo spazio \mathbb(R)^n non contiene più di n vettori linearmente indipendenti. Infatti, prendiamo k colonne da \mathbb(R)^n e creiamo da esse una matrice di dimensioni n\volte k. Se k>n, allora le colonne dipendono linearmente dal Teorema 3.4 dal rango della matrice. Quindi, \dim(\mathbb(R)^n)\leqslant n. Nello spazio \mathbb(R)^n non è difficile trovare n colonne linearmente indipendenti. Ad esempio, le colonne della matrice identità \mathbf(e)_1=\begin(pmatrix)1\\0\\\vdots\\0\end(pmatrix)\!,\quad \mathbf(e)_2= \begin(pmatrix)0\\1\ \\vdots\\0\end(pmatrix)\!,\quad \ldots,\quad \mathbf(e)_n= \begin(pmatrix) 0\\0\\\vdots\\1 \end(pmatrix)\ !. linearmente indipendenti. Quindi, \dim(\mathbb(R)^n)=n. Viene chiamato lo spazio \mathbb(R)^n Spazio aritmetico reale n-dimensionale. L'insieme di vettori specificato è considerato la base standard dello spazio \mathbb(R)^n . Allo stesso modo, è dimostrato \dim(\mathbb(C)^n)=n, quindi si chiama lo spazio \mathbb(C)^n Spazio aritmetico complesso n-dimensionale. 4. Ricordiamo che qualsiasi soluzione del sistema omogeneo Ax=o può essere rappresentata nella forma x=C_1\varphi_1+C_2\varphi_2+\ldots+C_(n-r)\varphi_(n-r), Dove r=\nomeoperatore(rg)A,UN \varphi_1,\varphi_2,\ldots,\varphi_(n-r)- sistema fondamentale di soluzioni. Quindi, \(Ax=o\)=\nomeoperatore(Lin) (\varphi_1,\varphi_2,\ldots,\varphi_(n-r)), cioè. la base dello spazio \(Ax=0\) delle soluzioni di un sistema omogeneo è il suo sistema fondamentale di soluzioni, e la dimensione dello spazio \dim\(Ax=o\)=n-r, dove n è il numero di incognite , e r è il rango della matrice del sistema. 5. Nello spazio M_(2\times3) delle matrici di dimensione 2\times3 si possono scegliere 6 matrici: \begin(gathered)\mathbf(e)_1= \begin(pmatrix)1&0&0\\0&0&0\end(pmatrix)\!,\quad \mathbf(e)_2= \begin(pmatrix)0&1&0\\0&0&0\end( pmatrix)\!,\quad \mathbf(e)_3= \begin(pmatrix) 0&0&1\\0&0&0\end(pmatrix)\!,\hfill\\ \mathbf(e)_4= \begin(pmatrix) 0&0&0\\ 1&0&0 \end(pmatrix)\!,\quad \mathbf(e)_5= \begin(pmatrix)0&0&0\\0&1&0\end(pmatrix)\!,\quad \mathbf(e)_6= \begin(pmatrix)0&0&0 \\0&0&1\end(pmatrix)\!,\hfill \end(raccolto) \alpha_1\cdot \mathbf(e)_1+\alpha_2\cdot \mathbf(e)_2+\alpha_3\cdot \mathbf(e)_3+ \alpha_4\cdot \mathbf(e)_4+\alpha_5\cdot \mathbf(e)_5+ \alpha_6\cdot \mathbf(e)_6= \begin(pmatrix)\alpha_1&\alpha_2&\alpha_3\\ \alpha_4&\alpha_5&\alpha_6\end(pmatrix) uguale alla matrice nulla solo nel caso banale \alpha_1=\alpha_2= \ldots= \alpha_6=0. Avendo letto l'uguaglianza (8.5) da destra a sinistra, concludiamo che qualsiasi matrice da M_(2\times3) è espressa linearmente attraverso le 6 matrici selezionate, cioè M_(2\times)= \operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_6). Quindi, \dim(M_(2\times3))=2\cdot3=6 e le matrici \mathbf(e)_1, \mathbf(e)_2,\ldots,\mathbf(e)_6 sono la base (standard) di questo spazio. Allo stesso modo, è dimostrato \dim(M_(m\volte n))=m\cdot n. 6. Per ogni numero naturale n nello spazio P(\mathbb(C)) dei polinomi a coefficienti complessi, si possono trovare n elementi linearmente indipendenti. Ad esempio, i polinomi \mathbf(e)_1=1, \mathbf(e)_2=z, \mathbf(e)_3=z^2,\,\ldots, \mathbf(e)_n=z^(n-1) sono linearmente indipendenti, essendo la loro combinazione lineare a_1\cdot \mathbf(e)_1+a_2\cdot \mathbf(e)_2+\ldots+a_n\cdot \mathbf(e)_n= a_1+a_2z+\ldots+a_nz^(n-1) uguale al polinomio zero (o(z)\equiv0) solo nel caso banale a_1=a_2=\ldots=a_n=0. Poiché questo sistema di polinomi è linearmente indipendente per qualsiasi numero naturale l, lo spazio P(\mathbb(C)) è infinitamente dimensionale. Allo stesso modo, concludiamo che lo spazio P(\mathbb(R)) dei polinomi a coefficienti reali ha dimensione infinita. Lo spazio P_n(\mathbb(R)) dei polinomi di grado non superiore a n è a dimensione finita. Infatti, i vettori \mathbf(e)_1=1, \mathbf(e)_2=x, \mathbf(e)_3=x^2,\,\ldots, \mathbf(e)_(n+1)=x^n formano una base (standard) di questo spazio, poiché sono linearmente indipendenti e qualsiasi polinomio di P_n(\mathbb(R)) può essere rappresentato come una combinazione lineare di questi vettori: a_nx^n+\ldots+a_1x+a_0=a_0\cdot \mathbf(e)_1+a_1 \mathbf(e)_2+\ldots+a_n\cdot \mathbf(e)_(n+1)Esempi di basi di spazi lineari
che sono linearmente indipendenti. Anzi, la loro combinazione lineare
7. Lo spazio C(\mathbb(R)) delle funzioni continue è infinitamente dimensionale. Infatti, per ogni numero naturale n i polinomi 1,x,x^2,\ldots, x^(n-1), considerate come funzioni continue, formano sistemi linearmente indipendenti (vedi esempio precedente).
Nello spazio T_(\omega)(\mathbb(R)) i binomi trigonometrici (di frequenza \omega\ne0 ) con base a coefficienti reali formano monomi \mathbf(e)_1(t)=\sin\omega t,~\mathbf(e)_2(t)=\cos\omega t. Sono linearmente indipendenti, poiché hanno l'identica uguaglianza a\sen\omega t+b\cos\omega t\equiv0 possibile solo nel caso banale (a=b=0). Qualsiasi funzione del modulo f(t)=a\sin\omega t+b\cos\omega t espressi linearmente attraverso quelli fondamentali: f(t)=a\,\mathbf(e)_1(t)+b\,\mathbf(e)_2(t).
8. Lo spazio \mathbb(R)^X delle funzioni reali definite sull'insieme X, a seconda del dominio di definizione di X, può essere a dimensione finita o infinita-dimensionale. Se X è un insieme finito, allora lo spazio \mathbb(R)^X è a dimensione finita (ad esempio, X=\(1,2,\ldots,n\)). Se X è un insieme infinito, allora lo spazio \mathbb(R)^X ha dimensione infinita (ad esempio, lo spazio \mathbb(R)^N delle sequenze).
9. Nello spazio \mathbb(R)^(+) qualsiasi numero positivo \mathbf(e)_1 diverso da uno può servire da base. Prendiamo, ad esempio, il numero \mathbf(e)_1=2 . Qualsiasi numero positivo r può essere espresso tramite \mathbf(e)_1 , cioè rappresentare nella forma \alpha\cdot \mathbf(e)_1\due punti r=2^(\log_2r)=\log_2r\ast2=\alpha_1\ast \mathbf(e)_1, dove \alpha_1=\log_2r . Pertanto, la dimensione di questo spazio è 1 e il numero \mathbf(e)_1=2 è la base.
10. Lascia \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_nè la base dello spazio lineare reale V. Definiamo funzioni scalari lineari su V ponendo:
\mathcal(E)_i(\mathbf(e)_j)=\begin(cases)1,&i=j,\\ 0,&i\ne j.\end(cases)
In questo caso, a causa della linearità della funzione \mathcal(E)_i, per un vettore arbitrario otteniamo \mathcal(E)(\mathbf(v))=\sum_(j=1)^(n)v_j \mathcal(E)(\mathbf(e)_j)=v_i.
Si definiscono quindi n elementi (covettori). \mathcal(E)_1, \mathcal(E)_2, \ldots, \mathcal(E)_n spazio coniugato V^(\ast) . Dimostriamolo \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n- base V^(\ast) .
Per prima cosa mostriamo che il sistema \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n linearmente indipendenti. Consideriamo infatti una combinazione lineare di questi covettori (\alpha_1 \mathcal(E)_1+\ldots+\alpha_n\mathcal(E)_n)(\mathbf(v))= e equipararlo alla funzione zero
\mathbf(o)(\mathbf(v))~~ (\mathbf(o)(\mathbf(v))=0~ \forall \mathbf(v)\in V)\colon~ \alpha_1\mathcal(E )_1(\mathbf(v))+\ldots+\alpha_n\mathcal(E)_n(\mathbf(v))= \mathbf(o)(\mathbf(v))=0~~\forall \mathbf(v )\in V.
Sostituendo in questa uguaglianza \mathbf(v)=\mathbf(e)_i,~ i=1,\ldots,n, noi abbiamo \alpha_1=\alpha_2\cdot= \alpha_n=0. Pertanto, il sistema degli elementi \mathcal(E)_1,\mathcal(E)_2,\ldots,\mathcal(E)_n lo spazio V^(\ast) è linearmente indipendente, poiché l'uguaglianza \alpha_1\mathcal(E)_1+\ldots+ \alpha_n\mathcal(E)_n =\mathbf(o) possibile solo in un caso banale.
In secondo luogo, dimostriamo che qualsiasi funzione lineare f\in V^(\ast) può essere rappresentata come una combinazione lineare di covettori \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n. Infatti, per qualsiasi vettore \mathbf(v)=v_1 \mathbf(e)_1+v_2 \mathbf(e)_2+\ldots+v_n \mathbf(e)_n per la linearità della funzione f otteniamo:
\begin(aligned)f(\mathbf(v))&= f(v_1 \mathbf(e)_1+\ldots+v_n \mathbf(e)_n)= v_1 f(\mathbf(e)_1)+\ldots+ v_n f(\mathbf(e)_n)= f(\mathbf(e)_1)\mathcal(E)_1(\mathbf(v))+ \ldots+ f(\mathbf(e)_n)\mathcal(E) _n (\mathbf(v))=\\ &=(f(\mathbf(e)_1)\mathcal(E)_1+\ldots+ f(\mathbf(e)_n)\mathcal(E)_n)(\mathbf ( v))= (\beta_1\mathcal(E)_1+ \ldots+\beta_n\mathcal(E)_n) (\mathbf(v)),\end(allineato)
quelli. la funzione f è rappresentata come una combinazione lineare f=\beta_1 \mathcal(E)_1+\ldots+\beta_n\mathcal(E)_n funzioni \mathcal(E)_1,\mathcal(E)_2,\ldots, \mathcal(E)_n(numeri \beta_i=f(\mathbf(e)_i)- coefficienti di combinazione lineare). Pertanto, il sistema covettore \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_nè una base dello spazio duale V^(\ast) e \dim(V^(\ast))=\dim(V)(per uno spazio a dimensione finita V ).
Se noti un errore, un errore di battitura o hai qualche suggerimento, scrivi nei commenti.
Un sottoinsieme di uno spazio lineare forma un sottospazio se è chiuso rispetto all'addizione di vettori e alla moltiplicazione per scalari.
Esempio 6.1. Un sottospazio in un piano forma un insieme di vettori i cui estremi giacciono: a) nel primo quarto; b) su una retta passante per l'origine? (l'origine dei vettori è all'origine delle coordinate)
Soluzione.
a) no, poiché l'insieme non è chiuso rispetto alla moltiplicazione per uno scalare: moltiplicato per un numero negativo, la fine del vettore cade nel terzo quarto.
b) sì, poiché sommando vettori e moltiplicandoli per un numero qualsiasi, le loro estremità rimangono sulla stessa retta.
Esercizio 6.1. I seguenti sottoinsiemi degli spazi lineari corrispondenti formano un sottospazio:
a) un insieme di vettori piani le cui estremità giacciono nel primo o nel terzo quarto;
b) un insieme di vettori piani i cui estremi giacciono su una retta che non passa per l'origine;
c) un insieme di linee di coordinate ((x 1, x 2, x 3)ï x 1 + x 2 + x 3 = 0);
d) insieme di linee coordinate ((x 1, x 2, x 3)ï x 1 + x 2 + x 3 = 1);
e) un insieme di linee di coordinate ((x 1, x 2, x 3)ï x 1 = x 2 2).
La dimensione di uno spazio lineare L è il numero dim L di vettori compresi in una qualsiasi delle sue basi.
Le dimensioni della somma e l'intersezione dei sottospazi sono legate dalla relazione
dim (U + V) = dim U + dim V – dim (U Ç V).
Esempio 6.2. Trova la base e la dimensione della somma e dell'intersezione dei sottospazi attraversati dai seguenti sistemi di vettori:
Soluzione Ciascuno dei sistemi di vettori che generano i sottospazi U e V è linearmente indipendente, cioè è una base del sottospazio corrispondente. Costruiamo una matrice dalle coordinate di questi vettori, disponendoli in colonne e separando un sistema da un altro con una linea. Riduciamo la matrice risultante alla forma graduale.
~ 
~ 
~ 
.
La base U + V è formata dai vettori , , , a cui corrispondono gli elementi iniziali della matrice a gradini. Pertanto dim (U + V) = 3. Allora
dim (UÇV) = dim U + dim V – dim (U + V) = 2 + 2 – 3 = 1.
L'intersezione dei sottospazi forma un insieme di vettori che soddisfano l'equazione (situati sui lati sinistro e destro di questa equazione). Otteniamo la base dell'intersezione utilizzando il sistema fondamentale di soluzioni del sistema di equazioni lineari corrispondente a questa equazione vettoriale. La matrice di questo sistema è già stata ridotta ad una forma graduale. Sulla base di ciò, concludiamo che y 2 è una variabile libera e poniamo y 2 = c. Allora 0 = y 1 – y 2, y 1 = c,. e l'intersezione dei sottospazi forma un insieme di vettori della forma 
= c(3, 6, 3, 4). Di conseguenza la base UÇV costituisce il vettore (3, 6, 3, 4).
Appunti. 1. Se continuiamo a risolvere il sistema, trovando i valori delle variabili x, otteniamo x 2 = c, x 1 = c, e sul lato sinistro dell'equazione vettoriale otteniamo un vettore uguale a quello ottenuto sopra .
2. Utilizzando il metodo indicato è possibile ottenere la base della somma indipendentemente dal fatto che i sistemi generatori di vettori siano linearmente indipendenti. Ma la base dell'intersezione sarà ottenuta correttamente solo se almeno il sistema che genera il secondo sottospazio è linearmente indipendente.
3. Se si determina che la dimensione dell'intersezione è 0, allora l'intersezione non ha base e non è necessario cercarla.
Esercizio 6.2. Trova la base e la dimensione della somma e dell'intersezione dei sottospazi compresi dai seguenti sistemi di vettori:
UN) 
B) 
Spazio euclideo
Lo spazio euclideo è uno spazio lineare su un campo R, in cui viene definita una moltiplicazione scalare che assegna ad ogni coppia di vettori , uno scalare , e sono soddisfatte le seguenti condizioni:
2) (a + b) = a() + b();
3) ¹Þ > 0.
Il prodotto scalare standard viene calcolato utilizzando le formule
(a 1 , … , a n) (b 1 , … , b n) = a 1 b 1 + … + a n b n.
I vettori e si dicono ortogonali, scritti ^ se il loro prodotto scalare è uguale a 0.
Un sistema di vettori si dice ortogonale se i vettori che lo compongono sono ortogonali a due a due.
Un sistema ortogonale di vettori è linearmente indipendente.
Il processo di ortogonalizzazione di un sistema di vettori, ..., consiste nella transizione ad un sistema ortogonale equivalente, ..., eseguita secondo le formule:
, dove , k = 2, … , n.
Esempio 7.1. Ortogonalizzare un sistema di vettori
= (1, 2, 2, 1), = (3, 2, 1, 1), = (4, 1, 3, -2).
Soluzione. Abbiamo = = (1, 2, 2, 1);
, = 
= = 1;
= (3, 2, 1, 1) – (1, 2, 2, 1) = (2, 0, -1, 0).
, = 
= =1;
= 
=1;
= (4, 1, 3, -2) – (1, 2, 2, 1) – (2, 0, -1, 0) = (1, -1, 2, -3).
Esercizio 7.1. Ortogonalizzare i sistemi vettoriali:
a) = (1, 1, 0, 2), = (3, 1, 1, 1), = (-1, -3, 1, -1);
b) = (1, 2, 1, 1), = (3, 4, 1, 1), = (0, 3, 2, -1).
Esempio 7.2. Sistema completo di vettori = (1, -1, 1, -1),
= (1, 1, -1, -1), alla base ortogonale dello spazio.
Soluzione: il sistema originale è ortogonale, quindi il problema ha senso. Poiché i vettori sono dati nello spazio quadridimensionale, dobbiamo trovare altri due vettori. Il terzo vettore = (x 1, x 2, x 3, x 4) è determinato dalle condizioni = 0, = 0. Queste condizioni danno un sistema di equazioni, la cui matrice è formata dalle linee coordinate dei vettori e . Risolviamo il sistema:
~ 
~ 
.
Alle variabili libere x 3 e x 4 può essere assegnato qualsiasi insieme di valori diverso da zero. Assumiamo, ad esempio, x 3 = 0, x 4 = 1. Quindi x 2 = 0, x 1 = 1 e = (1, 0, 0, 1).
Allo stesso modo, troviamo = (y 1, y 2, y 3, y 4). Per fare ciò, aggiungiamo una nuova linea di coordinate alla matrice passo-passo ottenuta sopra e la riduciamo alla forma passo-passo:
~ 
~ 
.
Per la variabile libera y 3 impostiamo y 3 = 1. Quindi y 4 = 0, y 2 = 1, y 1 = 0 e = (0, 1, 1, 0).
La norma di un vettore nello spazio euclideo è un numero reale non negativo.
Un vettore si dice normalizzato se la sua norma è 1.
Per normalizzare un vettore è necessario dividerlo per la sua norma.
Un sistema ortogonale di vettori normalizzati è detto ortonormale.
Esercizio 7.2. Completa il sistema di vettori ad una base ortonormale dello spazio:
a) = (1/2, 1/2, 1/2, 1/2), = (-1/2, 1/2, -1/2, 1/2);
b) = (1/3, -2/3, 2/3).
Mappature lineari
Siano U e V spazi lineari sul campo F. Una mappatura f: U ® V è detta lineare se e .
Esempio 8.1. Le trasformazioni dello spazio tridimensionale sono lineari:
a) f(x 1, x 2, x 3) = (2x 1, x 1 – x 3, 0);
b) f(x 1, x 2, x 3) = (1, x 1 + x 2, x 3).
Soluzione.
a) Abbiamo f((x 1, x 2, x 3) + (y 1, y 2, y 3)) = f(x 1 + y 1, x 2 + y 2, x 3 + y 3) =
= (2(x 1 + y 1), (x 1 + y 1) – (x 3 + y 3), 0) = (2x 1, x 1 – x 3, 0) + (2y 1, y 1 - y3,0) =
F((x 1, x 2, x 3) + f(y 1, y 2, y 3));
f(l(x 1 , x 2 , x 3)) = f(lx 1 , lx 2 , lx 3) = (2lx 1 , lx 1 – lx 3 , 0) = l(2x 1 , x 1 – x 3 , 0) =
Lf(x1, x2, x3).
Pertanto la trasformazione è lineare.
b) Abbiamo f((x 1 , x 2 , x 3) + (y 1 , y 2 , y 3)) = f(x 1 + y 1 , x 2 + y 2 , x 3 + y 3) =
= (1, (x 1 + y 1) + (x 2 + y 2), x 3 + y 3);
f((x 1 , x 2 , x 3) + f(y 1 , y 2 , y 3)) = (1, x 1 + x 2 , x 3) + (1, y 1 + y 2 , y 3 ) =
= (2, (x 1 + y 1) + (x 2 + y 2), x 3 + y 3) ¹ f((x 1, x 2, x 3) + (y 1, y 2, y 3) ).
Pertanto la trasformazione non è lineare.
L'immagine di una mappatura lineare f: U ® V è l'insieme delle immagini dei vettori da U, cioè
Im (f) = (f() ï О U). +…+ un m1
Esercizio 8.1. Trova il rango, il difetto, le basi dell'immagine e il nucleo della mappatura lineare f data dalla matrice:
a) A = ; b) A = ; c) A = 
.
Secondo la definizione di spazio lineare, quindi UN fosse un sottospazio è necessario verificarne la fattibilità UN operazioni:
1) : 
;
2) 
: 
;
e controlla che le operazioni siano in corso UN sono soggetti a otto assiomi. Tuttavia, quest’ultimo sarà ridondante (per il fatto che questi assiomi valgono in L), cioè è vero quanto segue
Teorema. Sia L uno spazio lineare su un campo P e 
. Un insieme A è un sottospazio di L se e solo se sono soddisfatti i seguenti requisiti:
Dichiarazione. Se l – N spazio lineare bidimensionale e UN il suo sottospazio, quindi UNè anche uno spazio lineare a dimensione finita e la sua dimensione non lo supera N.
P 
Esempio 1.
Un sottospazio dello spazio dei vettori dei segmenti V 2 è l'insieme S di tutti i vettori piani, ciascuno dei quali giace su uno degli assi coordinati 0x o 0y?
Soluzione: Permettere 
, 
E 
, 
. Poi 
. Quindi S non è un sottospazio 
.
Esempio 2.È un sottospazio lineare di uno spazio lineare V 2 ci sono molti vettori di segmenti piani S tutti i vettori piani il cui inizio e fine giacciono su una determinata retta l questo aereo?
Soluzione.
E 
vettore sli 
moltiplicare per un numero reale K, quindi otteniamo il vettore 
, anch'esso appartenente a S. Se 
E 
sono due vettori da S, allora 
(secondo la regola della somma dei vettori su una linea retta). Pertanto S è un sottospazio 
.
Esempio 3.È un sottospazio lineare di uno spazio lineare V 2 un mucchio di UN tutti i vettori piani le cui estremità giacciono su una data retta l, (assumiamo che l'origine di qualsiasi vettore coincida con l'origine delle coordinate)?
R 
decisione.
Nel caso in cui la linea retta l l'insieme non passa per l'origine UN sottospazio lineare dello spazio V 2
non lo è, perché 
.
Nel caso in cui la linea retta l
passa per l'origine, insieme UNè un sottospazio lineare dello spazio V 2
,
Perché 
e quando si moltiplica qualsiasi vettore 
ad un numero reale α
dal campo R noi abbiamo 
. Pertanto, i requisiti di spazio lineare per un insieme UN completato.
Esempio 4. Sia dato un sistema di vettori 
dallo spazio lineare l sopra il campo P. Dimostrare che l'insieme di tutte le possibili combinazioni lineari 
con probabilità 
da Pè un sottospazio l(questo è un sottospazio UNè chiamato il sottospazio generato da un sistema di vettori o guscio lineare questo sistema vettoriale, e indicato come segue: 
O 
).
Soluzione. Infatti, poiché , quindi per qualsiasi elemento X,
sì
UN abbiamo: 
, 
, Dove 
, 
. Poi
Da allora 
, Ecco perché 
.
Verifichiamo se è soddisfatta la seconda condizione del teorema. Se X– qualsiasi vettore da UN E T– qualsiasi numero da P, Quello . Perché il 
E 
,, Quello 
, , Ecco perché 
. Quindi, secondo il teorema, l'insieme UN– sottospazio dello spazio lineare l.
Per gli spazi lineari a dimensione finita è vero anche il contrario.
Teorema. Qualsiasi sottospazio UN spazio lineare l sopra il campo 
è l'estensione lineare di un sistema di vettori.
Quando si risolve il problema di trovare la base e la dimensione di un guscio lineare, viene utilizzato il seguente teorema.
Teorema. Base della shell lineare 
coincide con la base del sistema vettoriale. La dimensione del guscio lineare coincide con il rango del sistema di vettori.
Esempio 4. Trova la base e la dimensione del sottospazio 
spazio lineare R 3
[
X]
, Se 
, 
, 
, 
.
Soluzione. È noto che i vettori e le loro righe (colonne) di coordinate hanno le stesse proprietà (rispetto alla dipendenza lineare). Fare una matrice UN=
da colonne coordinate di vettori 
nella base 
.
Troviamo il rango della matrice UN.
. M 3
=
. 
.
Quindi il rango R(UN)=
3. Quindi, il rango del sistema di vettori è 3. Ciò significa che la dimensione del sottospazio S è 3 e la sua base è composta da tre vettori 
(poiché nella base minore 
sono incluse le coordinate solo di questi vettori).
Esempio 5. Dimostrare che l'insieme H vettori spaziali aritmetici 
, la cui prima e ultima coordinata sono 0, costituisce un sottospazio lineare. Trova la sua base e dimensione.
Soluzione. Permettere 
.
Quindi , e . Quindi, 
per ogni . Se 
, 
, Quello . Pertanto, secondo il teorema del sottospazio lineare, l'insieme Hè un sottospazio lineare dello spazio. Troviamo la base H. Considera i seguenti vettori da H: 
, 
, . Questo sistema di vettori è linearmente indipendente. Infatti, lasciamo che sia.
1. Sia il sottospazio l = l(UN 1 , UN 2 , …, e m) , questo è l– guscio lineare del sistema UN 1 , UN 2 , …, e m; vettori UN 1 , UN 2 , …, e m– il sistema di generatori di questo sottospazio. Quindi la base lè la base del sistema di vettori UN 1 , UN 2 , …, e m, cioè la base del sistema di generatori. Dimensione l pari al rango del sistema di generatori.
2. Sia il sottospazio lè la somma dei sottospazi l 1 e l 2. Un sistema di generazione di sottospazi per una somma può essere ottenuto combinando sistemi di generazione di sottospazi, dopo di che si trova la base della somma. La dimensione dell’importo è determinata dalla seguente formula:
debole(l 1 + l 2) = dimL 1 + dimL 2 – debole(l 1Ç l 2).
3. Sia la somma dei sottospazi l 1 e l 2 è dritto, cioè l = l 1Å l 2. In cui l 1Ç l 2 = {O) E debole(l 1Ç l 2) = 0. La base della somma diretta è uguale all'unione delle basi dei termini. La dimensione di una somma diretta è uguale alla somma delle dimensioni dei termini.
4. Diamo un esempio importante di sottospazio e varietà lineare.
Consideriamo un sistema omogeneo M equazioni lineari con N sconosciuto. Molte soluzioni M 0 di questo sistema è un sottoinsieme dell'insieme Rn ed è chiuso rispetto all'addizione di vettori e alla loro moltiplicazione per un numero reale. Ciò significa che ce ne sono molti M 0 – sottospazio dello spazio Rn. La base del sottospazio è l'insieme fondamentale delle soluzioni di un sistema omogeneo; la dimensione del sottospazio è uguale al numero di vettori nell'insieme fondamentale delle soluzioni del sistema.
Un mucchio di M soluzioni di sistema comuni M equazioni lineari con N anche le incognite sono un sottoinsieme dell'insieme Rn e uguale alla somma dell'insieme M 0 e vettore UN, Dove UNè una soluzione particolare del sistema originale e dell'insieme M 0 – insieme di soluzioni di un sistema omogeneo di equazioni lineari che accompagnano questo sistema (differisce da quello originale solo in termini liberi),
M = UN + M 0 = {UN = M, M Î M 0 }.
Ciò significa che molti Mè una varietà lineare dello spazio Rn con vettore di spostamento UN e direzione M 0 .
Esempio 8.6. Trova la base e la dimensione del sottospazio definito da un sistema omogeneo di equazioni lineari:
Soluzione. Troviamo una soluzione generale a questo sistema e al suo insieme fondamentale di soluzioni: 
Con 1 = (–21, 12, 1, 0, 0), Con 2 = (12, –8, 0, 1, 0), Con 3 = (11, –8, 0, 0, 1).
La base del sottospazio è formata da vettori Con 1 , Con 2 , Con 3, la sua dimensione è tre.
Fine del lavoro -
Questo argomento appartiene alla sezione:
Algebra lineare
Università statale di Kostroma intitolata a N. Nekrasov..
Se hai bisogno di materiale aggiuntivo su questo argomento, oppure non hai trovato quello che cercavi, ti consigliamo di utilizzare la ricerca nel nostro database delle opere:
Cosa faremo con il materiale ricevuto:
Se questo materiale ti è stato utile puoi salvarlo sulla tua pagina sui social network:
| Twitta |
Tutti gli argomenti in questa sezione:
BBK 22.174ya73-5
M350 Pubblicato per decisione del consiglio editoriale ed editoriale della KSU intitolata. N. A. Nekrasova Revisore A. V. Cherednikov
BBK 22.174ya73-5
ã T. N. Matytsina, E. K. Korzhevina 2013 ã KSU dal nome. NA Nekrasova, 2013
Unione (o somma)
Definizione 1.9. L'unione degli insiemi A e B è un insieme A È B, costituito da quelli e solo da quegli elementi che appartengono sebbene
Intersezione (o prodotto)
Definizione 1.10. L'intersezione degli insiemi A e B è un insieme AÇ B, che consiste di quelli e solo quegli elementi appartenenti allo stesso
Differenza
Definizione 1.11. La differenza tra gli insiemi A e B è l'insieme A B, costituito da quelli e solo quegli elementi che appartengono all'insieme A
Prodotto cartesiano (o prodotto diretto)
Definizione 1.14. Una coppia ordinata (o coppia) (a, b) è composta da due elementi a, b presi in un certo ordine. Coppie (a1
Proprietà delle operazioni sugli insiemi
Le proprietà delle operazioni di unione, intersezione e complemento sono talvolta chiamate leggi dell'algebra degli insiemi. Elenchiamo le principali proprietà delle operazioni sugli insiemi. Sia dato un insieme universale U
Metodo di induzione matematica
Il metodo dell'induzione matematica viene utilizzato per dimostrare affermazioni nella cui formulazione è coinvolto il parametro naturale n. Metodo di induzione matematica - metodo per dimostrare la matematica
Numeri complessi
Il concetto di numero è una delle principali conquiste della cultura umana. Prima sono comparsi i numeri naturali N = (1, 2, 3, …, n, …), poi gli interi Z = (…, –2, –1, 0, 1, 2, …), razionale Q
Interpretazione geometrica dei numeri complessi
È noto che i numeri negativi furono introdotti in connessione con la soluzione di equazioni lineari in una variabile. In compiti specifici, una risposta negativa veniva interpretata come il valore della quantità direzionale (
Forma trigonometrica di un numero complesso
Un vettore può essere specificato non solo dalle coordinate in un sistema di coordinate rettangolari, ma anche dalla lunghezza e
Operazioni sui numeri complessi in forma trigonometrica
È più conveniente eseguire addizioni e sottrazioni con numeri complessi in forma algebrica e moltiplicazioni e divisioni in forma trigonometrica. 1. Moltiplicazioni. Siano dati due k
Esponenziazione
Se z = r(cosj + i×sinj), allora zn = rn(cos(nj) + i×sin(nj)), dove n Î
Forma esponenziale di un numero complesso
Dall'analisi matematica si sa che e = , e è un numero irrazionale. Eile
Concetto di relazione
Definizione 2.1. Una relazione n-aria (o n-aria) P sugli insiemi A1, A2, …, An è un sottoinsieme qualsiasi
Proprietà delle relazioni binarie
Sia definita una relazione binaria P su un insieme non vuoto A, ovvero P Í A2. Definizione 2.9. Relazione binaria P su un insieme
Relazione di equivalenza
Definizione 2.15. Una relazione binaria su un insieme A si dice relazione di equivalenza se è riflessiva, simmetrica e transitiva. Rapporto equivalente
Funzioni
Definizione 2.20. Una relazione binaria ƒ Í A ´ B è detta funzione dall'insieme A all'insieme B se per qualsiasi x
Concetti generali
Definizione 3.1. Una matrice è una tabella rettangolare di numeri contenente m righe e n colonne. I numeri m e n sono chiamati ordine (o
Addizione di matrici dello stesso tipo
È possibile aggiungere solo matrici dello stesso tipo. Definizione 3.12. La somma di due matrici A = (aij) e B = (bij), dove i = 1,
Proprietà dell'addizione di matrici
1) commutatività: "A, B: A + B = B + A; 2) associatività: "A, B, C: (A + B) + C = A
Moltiplicazione di una matrice per un numero
Definizione 3.13. Il prodotto di una matrice A = (aij) per un numero reale k è una matrice C = (ñij), per cui c
Proprietà di moltiplicare una matrice per un numero
1) " A: 1×A = A; 2) " α, β О R, " A: (αβ)×A = α×(β×A) = β×
Moltiplicazione di matrici
Definiamo la moltiplicazione di due matrici; Per fare ciò è necessario introdurre alcuni concetti aggiuntivi. Definizione 3.14. Le matrici A e B si dicono coerenti
Proprietà della moltiplicazione di matrici
1) La moltiplicazione di matrici non è commutativa: A×B ≠ B×A. Questa proprietà può essere dimostrata con esempi. Esempio 3.6. UN)
Matrici trasposte
Definizione 3.16. La matrice At, ottenuta da una data sostituendo a ciascuna delle sue righe una colonna con lo stesso numero, si dice trasposta alla matrice A data
Determinanti di matrici del secondo e del terzo ordine
Ad ogni matrice quadrata A di ordine n è associato un numero, che è chiamato determinante di tale matrice. Denominazione: D, |A|, det A,
Definizione 4.6.
1. Per n = 1, la matrice A è composta da un numero: |A| = a11. 2. Sia noto il determinante di una matrice di ordine (n – 1). 3. Definire
Proprietà dei determinanti
Per calcolare determinanti di ordine maggiore di 3, utilizzare le proprietà dei determinanti e il teorema di Laplace. Teorema 4.1 (Laplace). Determinante di una matrice quadrata
Calcolo pratico dei determinanti
Un modo per calcolare i determinanti di ordine superiore a tre è espanderlo su qualche colonna o riga. Esempio 4.4 Calcolare il determinante D =
Il concetto di rango di matrice
Sia A una matrice di dimensione m ´ n. Selezioniamo arbitrariamente k righe e k colonne in questa matrice, dove 1 ≤ k ≤ min(m, n).
Trovare il rango di una matrice utilizzando il metodo dei minori confinanti
Uno dei metodi per trovare il rango di una matrice è il metodo di enumerazione dei minori. Questo metodo si basa sulla determinazione del rango della matrice. L'essenza del metodo è la seguente. Se c'è almeno un elemento ma
Trovare il rango di una matrice utilizzando trasformazioni elementari
Consideriamo un altro modo per trovare il rango di una matrice. Definizione 5.4. Le seguenti trasformazioni sono chiamate trasformazioni di matrici elementari: 1. moltiplicare
Il concetto di matrice inversa e metodi per trovarla
Sia data una matrice quadrata A. Definizione 5.7. La matrice A–1 è detta inversa della matrice A se A×A–1
Algoritmo per la ricerca della matrice inversa
Consideriamo uno dei modi per trovare la matrice inversa di un dato utilizzando le addizioni algebriche. Sia data una matrice quadrata A. 1. Trovare il determinante della matrice |A|. Unione Europea
Trovare la matrice inversa utilizzando trasformazioni elementari
Consideriamo un altro modo per trovare la matrice inversa utilizzando trasformazioni elementari. Formuliamo i concetti e i teoremi necessari. Definizione 5.11. Matrice Per nome
Metodo Cramer
Consideriamo un sistema di equazioni lineari in cui il numero di equazioni è uguale al numero di incognite, cioè m = n e il sistema ha la forma:
Metodo della matrice inversa
Il metodo della matrice inversa è applicabile ai sistemi di equazioni lineari in cui il numero di equazioni è pari al numero di incognite e il determinante della matrice principale non è uguale a zero. Forma matriciale della notazione di sistema
Metodo di Gauss
Per descrivere questo metodo, adatto a risolvere sistemi arbitrari di equazioni lineari, sono necessari alcuni nuovi concetti. Definizione 6.7. Equazione della forma 0×
Descrizione del metodo di Gauss
Il metodo di Gauss - un metodo di eliminazione sequenziale delle incognite - consiste nel fatto che, con l'aiuto di trasformazioni elementari, il sistema originale viene ridotto a un sistema equivalente di stepwise o t
Studio di un sistema di equazioni lineari
Studiare un sistema di equazioni lineari significa, senza risolvere il sistema, rispondere alla domanda: il sistema è coerente oppure no e, se è coerente, quante soluzioni ha? Rispondi a questo in
Sistemi omogenei di equazioni lineari
Definizione 6.11 Un sistema di equazioni lineari si dice omogeneo se i suoi termini liberi sono uguali a zero. Sistema omogeneo di m equazioni lineari
Proprietà delle soluzioni di un sistema omogeneo di equazioni lineari
1. Se il vettore a = (a1, a2, …, an) è una soluzione di un sistema omogeneo, allora il vettore k×a = (k×a1, k&t
Insieme fondamentale delle soluzioni di un sistema omogeneo di equazioni lineari
Sia M0 l'insieme delle soluzioni del sistema omogeneo (4) di equazioni lineari. Definizione 6.12. Vettori c1, c2, ..., c
Dipendenza e indipendenza lineare di un sistema di vettori
Sia a1, a2, …, am un insieme di m vettori n-dimensionali, a cui ci si riferisce solitamente come sistema di vettori, e k1
Proprietà di dipendenza lineare di un sistema di vettori
1) Il sistema di vettori contenente il vettore zero è linearmente dipendente. 2) Un sistema di vettori è linearmente dipendente se uno qualsiasi dei suoi sottosistemi è linearmente dipendente. Conseguenza. Se sì
Sistema vettoriale unitario
Definizione 7.13. Un sistema di vettori unitari nello spazio Rn è un sistema di vettori e1, e2, …, en
Due teoremi sulla dipendenza lineare
Teorema 7.1. Se un sistema di vettori più grande è espresso linearmente attraverso uno più piccolo, allora il sistema più grande è linearmente dipendente. Formuliamo questo teorema più in dettaglio: sia a1
Base e rango del sistema vettoriale
Sia S un sistema di vettori nello spazio Rn; può essere finito o infinito. S" è un sottosistema del sistema S, S" Ì S. Diamone due
Rango del sistema vettoriale
Diamo due definizioni equivalenti del rango di un sistema di vettori. Definizione 7.16. Il rango di un sistema di vettori è il numero di vettori in qualsiasi base di questo sistema.
Determinazione pratica del rango e della base di un sistema di vettori
Da questo sistema di vettori componiamo una matrice, disponendo i vettori come righe di questa matrice. Riduciamo la matrice alla forma a scaglioni utilizzando trasformazioni elementari sulle righe di questa matrice. A
Definizione di spazio vettoriale su un campo arbitrario
Sia P un campo arbitrario. Esempi di campi a noi noti sono il campo dei numeri razionali, reali e complessi. Definizione 8.1. Viene richiamato l'insieme V
Le proprietà più semplici degli spazi vettoriali
1) o – vettore zero (elemento), definito univocamente in uno spazio vettoriale arbitrario sul campo. 2) Per ogni vettore a О V esiste un unico
Sottospazi. Varietà lineari
Sia V uno spazio vettoriale, L Ì V (L è un sottoinsieme di V). Definizione 8.2. Sottoinsieme L del vettore pro
Intersezione e somma di sottospazi
Sia V uno spazio vettoriale sul campo P, L1 e L2 i suoi sottospazi. Definizione 8.3. Attraversando la subquest
Varietà lineari
Sia V uno spazio vettoriale, L un sottospazio, a un vettore arbitrario dello spazio V. Definizione 8.6
Spazi vettoriali a dimensione finita
Definizione 8.7. Uno spazio vettoriale V è detto n-dimensionale se contiene un sistema di vettori linearmente indipendente costituito da n vettori, e per
Base di uno spazio vettoriale a dimensione finita
V è uno spazio vettoriale a dimensione finita sul campo P, S è un sistema di vettori (finito o infinito). Definizione 8.10. La base del sistema S
Coordinate vettoriali relative ad una data base
Consideriamo uno spazio vettoriale V di dimensione finita di dimensione n, i vettori e1, e2, ..., ne costituiscono la base. Sia a un prodotto
Coordinate vettoriali in varie basi
Sia V uno spazio vettoriale n-dimensionale in cui sono date due basi: e1, e2, …, en – vecchia base, e"1, e
Spazi vettoriali euclidei
Dato uno spazio vettoriale V sul campo dei numeri reali. Questo spazio può essere uno spazio vettoriale a dimensione finita di dimensione n o a dimensione infinita
Prodotto scalare in coordinate
Nello spazio vettoriale euclideo V di dimensione n è data la base e1, e2, …, en. I vettori xey vengono scomposti in vettori
Concetti metrici
Negli spazi vettoriali euclidei, dal prodotto scalare introdotto si può passare ai concetti di norma vettoriale e di angolo tra vettori. Definizione 8.16. Norma (
Proprietà della norma
1) ||a|| = 0 Û a = o. 2) ||la|| = |l|×||a||, perché ||la|| =
Base ortonormale dello spazio vettoriale euclideo
Definizione 8.21. Una base di uno spazio vettoriale euclideo si dice ortogonale se i vettori della base sono ortogonali a due a due, cioè se a1, a
Processo di ortogonalizzazione
Teorema 8.12. In ogni spazio euclideo n-dimensionale esiste una base ortonormale. Prova. Siano a1, a2
Prodotto scalare in base ortonormale
Data una base ortonormale e1, e2, …, en dello spazio euclideo V. Poiché (ei, ej) = 0 per i
Complemento ortogonale del sottospazio
V è uno spazio vettoriale euclideo, L è il suo sottospazio. Definizione 8.23. Un vettore a si dice ortogonale al sottospazio L se il vettore
Relazione tra le coordinate di un vettore e le coordinate della sua immagine
Un operatore lineare j è dato nello spazio V, e la sua matrice M(j) si trova in qualche base e1, e2, …, en. Lascia che questa sia la base
Matrici simili
Consideriamo l'insieme Рn´n di matrici quadrate di ordine n con elementi provenienti da un campo arbitrario P. Su questo insieme introduciamo la relazione
Proprietà delle relazioni di similarità tra matrici
1. Riflessività. Qualsiasi matrice è simile a se stessa, cioè A ~ A. 2. Simmetria. Se la matrice A è simile a B, allora B è simile ad A, cioè
Proprietà degli autovettori
1. Ogni autovettore appartiene a un solo autovalore. Prova. Sia x un autovettore con due autovalori
Polinomio caratteristico di una matrice
Data una matrice A О Рn´n (o A О Rn´n). Definire
Condizioni nelle quali una matrice è simile a una matrice diagonale
Sia A una matrice quadrata. Possiamo supporre che questa sia una matrice di un operatore lineare definito in qualche base. È noto che in un'altra base la matrice dell'operatore lineare
Forma normale di Jordan
Definizione 10.5. Una cella di Jordan di ordine k relativa al numero l0 è una matrice di ordine k, 1 ≤ k ≤ n,
Riduzione di una matrice alla forma Jordan (normale).
Teorema 10.3. La forma normale di Jordan è determinata univocamente per una matrice fino all'ordine di disposizione delle celle di Jordan sulla diagonale principale. Eccetera
Forme bilineari
Definizione 11.1. Una forma bilineare è una funzione (mappatura) f: V ´ V ® R (o C), dove V è un vettore arbitrario
Proprietà delle forme bilineari
Qualsiasi forma bilineare può essere rappresentata come una somma di forme simmetriche e antisimmetriche. Con la base selezionata e1, e2, …, en nel vettore
Trasformazione di una matrice di forma bilineare quando si passa ad una nuova base. Rango della forma bilineare
Siano due basi e = (e1, e2, …, en) e f = (f1, f2,
Forme quadratiche
Sia A(x, y) una forma bilineare simmetrica definita sullo spazio vettoriale V. Definizione 11.6
Riduzione di una forma quadratica a forma canonica
Data la forma quadratica (2) A(x, x) = , dove x = (x1
Legge d'inerzia delle forme quadratiche
È stato stabilito che il numero di coefficienti canonici diversi da zero di una forma quadratica è uguale al suo rango e non dipende dalla scelta di una trasformazione non degenere con l'aiuto della quale la forma A(x
Condizione necessaria e sufficiente per il segno di una forma quadratica
Dichiarazione 11.1. Affinché la forma quadratica A(x, x), definita nello spazio vettoriale n-dimensionale V, sia definita in segno, è necessario
Condizione necessaria e sufficiente per la forma quadratica quasi alternata
Dichiarazione 11.3. Affinché la forma quadratica A(x, x), definita nello spazio vettoriale n-dimensionale V, sia quasi-segno alternato (cioè,
Criterio di Sylvester per il segno definito di una forma quadratica
Sia determinata la forma A(x, x) nella base e = (e1, e2, …, en) dalla matrice A(e) = (aij)
Conclusione
L'algebra lineare è una parte obbligatoria di qualsiasi programma di matematica superiore. Ogni altra sezione presuppone la presenza di conoscenze, competenze e abilità sviluppate durante l'insegnamento di questa disciplina
Bibliografia
Burmistrova E.B., Lobanov S.G. Algebra lineare con elementi di geometria analitica. – M.: Casa editrice HSE, 2007. Beklemishev D.V. Corso di geometria analitica e algebra lineare.
Algebra lineare
Manuale didattico e metodologico Redattore e correttore di bozze G. D. Neganova Dattilografia computerizzata di T. N. Matytsina, E. K. Korzhevina
