אִמָא. אינטגרלי משטח מהסוג השני

מינימום תיאורטי

נושא זה ממשיך את הדיון באינטגרלים עקומים ומשטחים שהתחיל בנושא "". מומלץ להכיר את הנושא מראש. בשל המורכבות הגדולה יותר של הנושא, אינטגרלים עקומים ומשטחים
הסוג השני נחשב בנפרד. אינטגרלי שטח מהסוג השני נדונים כאן - אולי הפעולה האינטגרלית המורכבת ביותר ב
ניתוח פונקציות של משתנים רבים. התוכנית תהיה דומה לחלוטין לשיקול של אינטגרל עקום מהסוג השני. נתחיל עם יישומים פיזיים,
ולאחר מכן נעבור להיבט המתמטי הפורמלי.

1. יישומים פיזיים של אינטגרל פני השטח מהסוג השני

הדרך הטבעית ביותר להציג אינטגרל משטח מהסוג השני היא לשקול את זרימת הנוזל דרך משטח כלשהו. נתחיל עם מקרה פשוט:
הנוזל זורם לאורך ציר ה-X במהירות קבועה. הבה נבחר אזור מאונך לזרימה ונמצא את מסת הנוזל העובר דרכו
אותה בזמן. במהלך הזמן הזה, "מקביל" עם גובה ושטח בסיס של. המסה של ה"מקביל" הזה
שווה ל , היכן צפיפות הנוזל.

כעת תנו לנוזל לזרום במקביל למישור בזווית לציר ה-x, אך עדיין במהירות. האתר מהקודם
במקרה עדיין נמקם אותו בניצב לציר האבשסיס. עם הזמן, "מקביל" נוטה עובר דרכו (ראה איור 1). המסה שלו
שווה ל . שימו לב שהכנסת וקטור יחידה נורמלי לאתר מאפשרת לנו לכתוב .
מוכנס וקטור פורמלי של אזור יסודי, שהמודלוס שלו שווה ל , וכיוונו עולה בקנה אחד עם כיוון הווקטור
רגיל לאתר. לאחר מכן . סימון זה מאפשר לך לא לדאוג לגבי הכיוון של וקטור מהירות הנוזל ביחס אליו
לאתר.

נותר לנטוש את הקטנות של השטח שדרכו זורם הנוזל, ואת ההנחה של מודול וכיוון מהירות קבועים. לאחר מכן
פני השטח מחולקים לחלקים קטנים, שבתוכם וקטור המהירות יכול להיחשב קבוע. מסת הנוזל העובר דרך פני השטח היא
נתון בערך על ידי הסכום
.
הנוסחה המדויקת תתקבל במגבלה של חלוקת פני השטח לחלקים אינסופיים. הגבול הוא אינטגרל משטח מהסוג השני:
.
בעת כתיבת חלק זה נעשה שימוש בקטע של חומר חינוכי של מורה מהמחלקה לפיזיקה כללית, המשמש אותו בשיעורי סמינריון.

2. הגדרה של אינטגרל משטח מהסוג השני

עכשיו לגבי הבנייה הרשמית של האינטגרל. בשל העובדה שהשדה הווקטור משולב על פני השטח, הגיוני להבהיר באיזה צד
משטח, האינטגרל מחושב (כמו בחישוב זרימת נוזל: נוזל זורם אל פני השטח או זורם ממנו). לכן, זה מצוין במיוחד
שהמשטח שעליו מתבצע האינטגרציה חייב להיות דו-צדדי או ניתן לכיוון (כלומר רצועת Möbius בכללותה לא תעבוד). משטח
מכוון מיד, כלומר. נבחר כיוון מסוים של הנורמלי אל פני השטח (לדוגמה, אם האינטגרל מחושב על פני כדור, אז הנורמלי יכול להיות
מכוון מהכדור או לתוך הכדור). רכיבי השדה הם, במקרה הכללי, פונקציות של נקודה. משטח של אינטגרציה
מחולק לחלקים קטנים, בוחרים נקודה בכל חלק ומרכיבים את הסכום
,
היכן שטח ההקרנה של האלמנט על המטוס, האם שטח ההקרנה של האלמנט הזה על המטוס, האם השטח
הקרנה של אלמנט זה על מישור. אנו מבצעים את הסיכום על כל האלמנטים שאליהם מחולקים פני השטח:

וללכת עד הגבול, לכוון את הקוטר של האזור החלקי הגדול ביותר לאפס. הגבול הוא אינטגרל משטח מהסוג השני
.

הבה נראה כיצד לצמצם את האינטגרל הזה לטופס משלב 1. כדי לעשות זאת, תצטרך לבצע סטייה קטנה בעלת אופי גיאומטרי גרידא. יִהיֶה
מישור החותך את צירי הקואורדינטות (ראה איור 2). לחלק של המטוס הזה שנמצא באוקטנט הראשון יש שטח של. אתה צריך למצוא את האזור
כל שלוש ההקרנות האורתוגונליות של חלק נתון של המישור על גבי מישורי קואורדינטות. כידוע, שטח ההקרנה של דמות שווה למכפלת השטח
הדמות עצמה והקוסינוס של הזווית בין מישור הדמות למישור שעליו היא מוקרנת (ראה איור 3). הָהֵן. צריך למצוא את הזוויות שעושות
מטוס עם מטוסי קואורדינטות. הזווית בין שני מישורים שווה לזווית שבין הנורמליות שלהם. היחידה הנורמלית למישור כוללת רכיבים,
שהם קוסינוס הכיוון שלו. לכן, הזווית בין המישור למישור שווה (ראה איור 2), ולכן .
אותו קשר יהיה תקף לאזורים אינפיניטימליים: . ובדומה לכך.
בהתחשב ביחסים אלה, האינטגרל מקבל את הצורה
.
אגב, צורת ההקלטה הזו היא יותר ויזואלית, אז נעבוד איתה.

היפוך כיוון הנורמלי גורם לאינטגרל לשנות סימן.

3. חישוב אינטגרל פני השטח מהסוג השני

לאחר הפחתת האינטגרל לצורה המכילה את כיוון הקוסינוס של הנורמלי אל פני השטח, הבעיה מצטמצמת למעשה לכתיבת היחידה רגילה
עם חישוב נוסף של אינטגרל פני השטח מהסוג הראשון. יש כמה פרטים בפעולות אלה, אז בואו נסתכל על החישוב בפירוט
אינטגרלים מסוג זה.

נתחיל מהמקרה שבו משטח האינטגרציה ניתן על ידי משוואה מפורשת, למשל, . ואז הווקטור הנורמלי נכתב כך:
,
ואלמנט שטח הפנים
.
כתוצאה מכך, אינטגרל פני השטח מקבל את הצורה הבאה:
, (1)
היכן האזור של המישור אליו מוקרן משטח האינטגרציה.

יכול להיות שמשטח האינטגרציה מוקרן בצורה נכונה על המישור (ונתון על ידי המשוואה) או על המישור
(וניתנת על ידי המשוואה ). ואז הנוסחה שלפיה מחושב האינטגרל מותאמת מעט:
(2)
אוֹ
. (3)
כמובן, לא מומלץ לשנן נוסחאות כאלה: קל לבלבל משהו - עדיף לשחזר אותן ביחס לספציפי
חישוב שוב, בהתבסס על הנוסחה של הווקטור הרגיל והשטח של אלמנט משטח קטן.

יש מקרה אחד מודגש כאשר המשטח מוקרן בצורה נכונה על כל שלושת מישורי הקואורדינטות, כלומר. ממשוואת פני השטח כל משתנה
יכול להתבטא בצורה חד משמעית. אז החישוב מפושט באופן משמעותי. שימו לב למבנה הנוסחאות (1) - (3). בכל אחד מהם יש שלושה
מונחים, ואחד מהם נראה פשוט יותר מהאחרים. כאשר מקרינים משטח על מישור, מונח זה מכיל את הרכיב
שדות ; כאשר מוקרן על מישור, זהו המונח המכיל את הרכיב; כאשר מוקרנים על מטוס, זה המונח
רכיב המכיל. אם המשטח מקרין בצורה נכונה על מישור קואורדינטות כלשהו, ​​אז אנחנו מפצלים את האינטגרל
לשלושה חלקים ולעצב כל חלק בצורה הנוחה ביותר:
.

לבסוף, המקרה של הגדרה פרמטרית של פני השטח
.
כמו בעת חישוב אינטגרל משטח מהסוג הראשון, יש להתחשב בשלושה יעקוביאנים:
.
קוסינוס הכיוון של הנורמלי באים לידי ביטוי דרכם:
,
אלמנט משטח
.
לפיכך, עבור האינטגרל שאנו מקבלים
,
היכן טווח השינויים בפרמטרים המתאים למשטח האינטגרציה.

4. נוסחת סטוקס. נוסחת אוסטרוגרדסקי-גאוס

אינטגרל פני השטח מהסוג השני קשור לשתי נוסחאות המוצאות יישומים שונים, כולל ביישומים פיזיים.
נוסחת סטוקס:
,
איפה ,
המשטח נמתח על קו המתאר, חציית קו המתאר תואמת את בחירת הנורמלי למשטח לפי כלל הבורג הימני.
נדרשות הבהרות אם למשטח האינטגרציה יש "חורים".
הנוסחה של גרין היא מקרה מיוחד של הנוסחה הזו. בנוסף, מנוסחת סטוקס היא עוקבת אחר התנאי לעצמאותו של האינטגרל העקמומי של השני
סוג של צורת השביל.

נוסחת אוסטרוגרדסקי-גאוס.
עבור שדה וקטור הנוסחה מתגשמת

שבו המשטח מגביל את הנפח.

לנוסחת אוסטרוגרדסקי-גאוס יש יישומים שונים. בואו נסתכל על שניים מהם. ראשית, קל להוכיח שניתן לחשב נפח של גוף
לפי הנוסחה

שנית, לפעמים יש צורך לחשב אינטגרל משטח מהסוג השני על פני משטח פתוח, הכרוך בחישובים מסורבלים.
לאחר מכן סוגרים את המשטח, מומר את האינטגרל למשולש, ומחסרים את האינטגרל על פני המשטח שנוסף (ראה דוגמה למטה).

הערה. הנוסחאות של סטוקס ואוסטרוגרדסקי-גאוס נכתבות בצורה נוחה יותר בניתוח וקטור תוך שימוש בסלסול והדיברגנציה של השדה הווקטורי.

דוגמאות לחישוב אינטגרלי משטח מהסוג השני

דוגמה 1. אינטגרל מטוס.. אז נקבל) חלקים מפרבולואיד אליפטי (תקין חיצוני).

הבה נכתוב מחדש את האינטגרל בטופס
.
משטח האינטגרציה - פרבולואיד אליפטי - מוקרן בצורה נכונה רק על המישור, ולכן אנו כותבים את משוואת פני השטח בצורה
.
מצא את הווקטור הנורמלי של היחידה:
.

ניתן להכליל בקלות את הרעיון של אינטגרל כפול על אזור שטוח למקרה של אינטגרציה על פני משטח. תן (S) להיות משטח (סגור או פתוח) ופונקציה מתמשכת של נקודה על משטח זה. שברו (S) לחלקים

ולאפשר את השטחים של חלקים אלה וכל נקודות הממוקמות בחלקים אלה. הידור של סכום המוצרים

הגבול של סכום זה עם עלייה אינסופית במספר החלוקים וירידה אינסופית בכל אחד מהחלקים נקרא האינטגרל של הפונקציה על פני השטח

הבה נניח שקווים ישרים מקבילים לציר Z חוצים את פני השטח בנקודה אחת בלבד (איור 48) ונניח להקרנה (S) להיות במישור XOY. באמצעות נוסחה (26), הקובעת את הקשר בין שטח הפנים היסודי (S) לבין השטח המקביל של הקרנתו, נוכל לצמצם את האינטגרל על פני השטח (S) לאינטגרל על פני השטח השטוח:

במקרה זה, ההנחה היא שהיא שונה מאפס ושערך הפונקציה בנקודה N של האזור עולה בקנה אחד עם הערך של הפונקציה שצוינה על פני השטח באותה נקודה M, שהשלכתה עולה בקנה אחד עם . אם משוואת המשטח (S) ניתנת בצורה מפורשת (22) והפונקציה באה לידי ביטוי במונחים של הקואורדינטות, אזי כאשר אינטגרציה מעליה די בהחלפת הפונקציה בביטוי. המכנה בצד ימין של (29) נקבע על ידי השלישי של הנוסחאות (24).

שים לב שלאינטגרלים פני השטח יש כמובן את כל המאפיינים של אינטגרל כפול המצוין ב , בפרט, משפט הערך הממוצע מתקיים עבורם.

הבה נוכיח כעת את אחת הנוסחאות המרכזיות בתורת האינטגרלים המרובים - נוסחת אוסטרוגרדסקי, הקובעת קשר בין האינטגרל המשולש על פני נפח לבין האינטגרל על פני השטח (S) התוחם נפח זה. נשקול כיצד והיכן ישרים מקבילים לציר Z מצטלבים (S) בלא יותר משניים

נקודות. הבה נשמור על אותו סימון כמו באיור. 40. הבה ניקח בחשבון גם את כיוון הנורמלי אל (S), ונניח שהוא מכוון מחוץ לנפח (V) (נורמלי חיצוני) (איור 50). כיוון זה יוצר זווית חדה עם ציר OZ בחלק העליון של המשטח (I), וזווית קהה בחלק התחתון (I). לכן, בחלק התחתון, נציין כי על קו המגע של המשטח (5) עם הגליל הבולט (איור 50). נוסחה (26) נותנת

תנו, יחד עם הנגזרת, להיות רציפים באזור עד (S). הבה נבחן את האינטגרל המשולש של הפונקציה.באמצעות נוסחה (16), יהיה לנו

אבל האינטגרל של הנגזרת שווה להפרש בין ערכי הפונקציה האנטי-נגזרת בגבול העליון והתחתון:

החלפה לפי נוסחאות (30), אנו מצמצמים אינטגרציה לאינטגרציה מעל (S), ובאינטגרל הראשון, המכיל את האורדינאטה המשתנה של חלק (I) של פני השטח (S), נצטרך להשתמש בראשון של הנוסחאות (30), ונקבל את האינטגרל מעל (II ), באינטגרל השני המכיל תצטרך להשתמש בשני של נוסחאות (30), ותקבל את האינטגרל מעל (I):

לא ניתן עוד לכתוב את הסמלים של z, מכיוון שמצוין על איזה חלק של פני השטח האינטגרציה מתבצעת. בצד ימין מופיע סכום האינטגרלים על חלקים (II) ו-(I), כלומר האינטגרל על השלם

משטחים (S):

אם הן פונקציות שיש להן את המאפיינים של פונקציה R, אז, תוך התחשבות בכך

בהתבסס על (31), נוכל לכתוב את הנוסחה לאינטגרציה לפי חלקים:

בדיוק באותו אופן, אם נוכל להוכיח שני פונקציות אחרות

בהוספת שלוש הנוסחאות שהתקבלו מונח אחר מונח, אנו מגיעים לנוסחה של אוסטרוגרדסקי

בדומה ל-(31,), אינטגרציה לפי חלקים נכתבות נוסחאות לנגזרות ביחס ל-x ו-y.

למען הקיצור, לא נכתוב כאן את הארגומנטים x, y, z של הפונקציות P, Q, אלא יש לזכור שמדובר בפונקציות המוגדרות בנפח ורציפות עם הנגזרות שלהן.

בפרק הבא ניתן מספר רב של דוגמאות ליישום נוסחת אוסטרוגרדסקי.

כמויות הן פונקציות המוגדרות על פני השטח (S). ראינו אותם רציפים. אפשר להניח הנחה כללית יותר, כלומר, להניח ש-(S) מחולק למספר סופי של חלקים, שעל כל אחד מהם הפונקציות המצוינות הן רציפות. זה יהיה המקרה, למשל, אם (S) הוא פולידרון.

בעת גזירת הנוסחה (31), הנחנו כי ישרים מקבילים לציר חותכים את פני השטח (S) של האזור בשתי נקודות לכל היותר. לא קשה להכליל את הנוסחה הזו לאזורים בעלי צורה כללית יותר. נציין קודם כל שאם לפני השטח (S), בנוסף לחלק העליון (II) ולחלק התחתון (I), יש חלק צד גלילי עם גנרטריצות מקבילות לציר, אז בחלק הצדדי הזה ומוסיפים חלק זה בצד ימין של הנוסחה (31) אינו משנה את הערך של אינטגרל פני השטח, כך שכל ההוכחה של הנוסחה נשארת תקפה. במקרה כללי יותר, מספיק להשתמש במשטחים גליליים עם מחוללים מקבילים לציר כדי לחלק למספר סופי של חלקים העומדים בתנאים הקודמים, ולהחיל נוסחה (31) על כל חלק. הוספת הנוסחאות המתקבלות בצורה זו, יהיה לנו בצד שמאל אינטגרל משולש על כל הנפח. בצד ימין יהיה לנו סכום האינטגרלים על כל המשטחים של אותם חלקים שאליהם חילקנו (v). האינטגרלים על פני משטחי העזר הגליליים המופחתים, כפי שצוין לעיל, שווים לאפס. כך, כתוצאה מהוספה בצד ימין, יהיה לנו אינטגרל על פני השטח (S) של הכרך המקורי. אז מסתבר שנוסחה (31) תקפה עבור תחומים בעלי צורה כללית יותר.

הבה נבחן אינטגרלים של פונקציות המוגדרות על משטחים, מה שנקרא אינטגרלים משטחיים. תורת האינטגרלים של פני השטח דומה במובנים רבים לתיאוריית האינטגרלים העקומים. ישנם אינטגרלים משטחים של הראשון ו

מהסוג השני.

4.1. אינטגרלי משטח מהסוג הראשון. תן לפונקציה f(x, y, z)

מוגדר על משטח חלק חלק חתיכות S, תחום על ידי קו מתאר חלק חלק חתיכות (איור 4.1). בואו נשבור את זה

בהתאמה ∆ s 1, ∆ s 2 ..., ∆ s n. ניקח נקודה שרירותית M i (x i, y i, z i) בתוך כל חלק S i, i = 1, n, אנו מחשבים את ערך הפונקציה בה ונעשה את הסכום הבא:

σ n= ∑ f (x i, y i, z i) ∆ s i
i=1		עבור הפונקציה f (x, y, z) by
מה שנקרא אינטגרל
משטח S.
הגבול הסופי של זה		תוך כדי חתירה
ה-λ הגדול ביותר מבין הקוטרים של כל המשטחים החלקיים S i
				1, נ

אם הוא קיים ואינו תלוי לא בשיטת חלוקת המשטח לחלקיות או בבחירת הנקודות, אז זה נקרא אינטגרל פני השטח מהסוג הראשון (מעל שטח הפנים)מהפונקציה

f (x, y, z) לאורך פני השטח S והוא מסומן בסמל		∫∫ f(x, y, z) ds.
אז בהגדרה
	= ∫∫ f(x, y, z) ds.
I = lim ∑ f(xi , yi , zi ) ∆ si
λ → 0i = 1

אינטגרל פני השטח מהסוג הראשון הוא הכללה של האינטגרל הכפול, ולכן התנאים לקיומו של האינטגרל הכפול ותכונותיו מועברים בקלות לאינטגרל פני השטח מהסוג הראשון.

חישוב אינטגרלים משטחים מהסוג הראשון מפחית לחישוב אינטגרלים כפולים: מבוסס על משוואת פני השטחס,

האינטגרנד הופך לשני משתנים, שטווחם יהיה הקרנת פני השטח S על מישור הקואורדינטות המתאים למשתנים אלו.

תנו למשטח S להיות מוגדר על ידי המשוואה z = z (x, y) ו-z (x, y) יהיו רציפים יחד עם הנגזרות החלקיות שלו z ′ x, z ′ y בתחום סגור S xy, שהוא השלכה של המשטח S על מישור הקואורדינטות xOy, אז

∫∫ f(x, y, z) ds= ∫∫ f(x, y, z(x, y)) 1 + (z′ x ) 2 + (z′ y ) dxdy.
	S xy

נוסחה זו מבטאת את אינטגרל פני השטח מהסוג הראשון דרך האינטגרל הכפול על הקרנה של פני השטח S על מישור הקואורדינטות xOy.

אינטגרלי פני השטח מהסוג הראשון על פני השטח S מחושבים בצורה דומה באמצעות אינטגרלים כפולים על ההקרנות שלו על

מישורי תיאום xOz ו-yOz בהתאמה:
∫∫ f (x ,y ,z )ds = ∫∫ f (x ,y (x ,z ),z )		1+ (y ′ x )2 + (y ′ z )dxdz ,
	S xz
∫∫ f (x, y,z)ds= ∫∫ f (x(y,z), y,z)		1 + (x′ y )2 + (x′ z )dydz.
	S yz

באמצעות אינטגרלי משטח מהסוג הראשון, ניתן לחשב את שטח הפנים וכן מסה, מומנטים סטטיים, מומנטים של אינרציה וקואורדינטות של מרכז המסה עבור משטחי חומר בעלי צפיפות חלוקת מסה משטחית ידועה.

דוגמה 4.1. לחשב

∫∫ 1 + 4 x 2 + 4 y 2 ds , כאשר S הוא חלק מהפרבו-

loid של סיבוב z = 1 − x 2 − y 2 , מנותק על ידי המישור z = 0 .

פִּתָרוֹן. בואו לעצב את המשטח

S למטוס xOy .

ההשלכה S xy היא מעגל התחום על ידי המעגל x 2 + y 2 = 1 (איור.

4.2). נחשב את אינטגרל פני השטח הנתון באמצעות נוסחה (4.2), שעבורה נמצא z ′ x = − 2 x , z ′ y = − 2 y . ואז, התחייבות כפולה

בלתי נפרד			אל הקוטב	קואורדינטות,							S xy הוא מעגל,
	1 +4 x 2 +4 y 2 ds =∫∫			1+ 4x 2 + 4y 2					1 + 4 x2 + 4 y2 dxdy=
			S xy
			= ∫∫ (1 +4 x 2 +4 y 2) dxdy =
			S xy
	= ∫ d ϕ ∫ (1 +4 ρ 2 ) ρ d ρ =∫							+ ρ 4)	d ϕ=		∫d ϕ .

4.2. משטחים דו צדדיים. המשטח S נקרא

דו צדדי, אם חוצים לאורך כל קו מתאר סגור השוכב על פני השטח S ולא חותכים את גבולותיו, כאשר חוזרים לנקודת ההתחלה, אינו משנה את כיוון הנורמלי אל פני השטח. אחרת, המשטח נקרא חד צדדי. דוגמאות למשטחים דו-צדדיים: מישור, כדור וכל משטח המוגדר על ידי המשוואה z = z (x, y), כאשר z = z (x, y), z ′ x (x, y), z ′ y (x , y) - רציף באזור מסויםG. דוגמה למשטח חד צדדי היא רצועת מוביוס.

4.3. אינטגרל משטח מהסוג השני. תן ל-S - משטח חלק נתון על ידי המשוואה z = z(x, y) והפונקציה f(x, y, z)

מוגדר בנקודות של פני השטח S.

בוא נבחר את אחת מצלעות המשטח, כלומר, אחד משני כיוונים אפשריים של הנורמלי בנקודות של המשטח (כך כיוונו את המשטח). אם הנורמלים עושים זוויות חדות עם

ציר עוז , אז נדבר עלהצד העליון של המשטח (בערך הכיוון החיובי של הנורמלי ), ואם הנורמליים הם -זוויות קהות עם ציר עוץ, אז אנחנו מדברים על הצד התחתון של פני השטח (הכיוון השלילי של הנורמלי).

הבה נחלק את פני השטח S באופן שרירותי ל-n חלקים S 1, S 2 ..., S n, ודרך (S xy) i נסמן את ההשלכה של החלק ה-i של המשטח

למטוס xOy. בתוך כל משטח חלקי S i, i = 1, n, בחר נקודה שרירותית M i (x i, y i, z i) וחשב את ערך הפונקציה

בו נעשה את הסכום

σ n= ∑ f (x i, y i, z i) ∆ s i, i = 1

כאשר ∆ s i - area(S xy) i, נלקח עם סימן פלוס אם הצד העליון של המשטח S נבחר ועם סימן מינוס אם הצד התחתון נבחר

משטח S. לsumσ n הזה קוראים סכום אינטגרליעבור הפונקציה f(x, y, z).

הגבול הסופי I של הסכום האינטגרלי, כ-λ הגדול ביותר מכל קוטרי ההקרנה (S xy) i שואף לאפס, אם הוא קיים

אינו תלוי בשיטת חלוקת המשטח S או בבחירת הנקודות

M i (x i, y i, z i), אז הגבול הזה נקרא אינטגרל פני השטח של הסוג השני של פונקציה f(x, y, z) לאורך הצד הנבחר של פני השטח לפי משתנים x ו-y ומסומנים ב-∫∫ f (x, y, z) dxdy. לפיכך, לפי

הַגדָרָה

משטח S במשתנים x ו-y.

באופן דומה, ניתן להגדיר אינטגרלי משטח מהסוג השני על צד נבחר של פני השטח S במשתנים y ו-z, במשתנים x ו-z:

∫∫ f(x, y, z) dydz,	∫∫ f(x, y, z) dxdz.

תנו ל-P (x, y, z), Q (x, y, z), R (x, y, z) להיות פונקציות הניתנות לשילוב מעל

משטח S במשתנים y ו-z, x ו-z, x ו-y, בהתאמה. סכום האינטגרלים

∫∫ P(x, y, z) dydz,	∫∫ Q(x, y, z) dxdz,	∫∫ R(x, y, z) dxdy
נקרא אינטגרל כללי מהסוג השני ומסומן
∫∫ P(x, y, z) dydz+ Q(x, y, z) dxdz+ R(x, y, z) dxdy.

מכיוון שאנו רואים במשטח S דו צדדי והאינטגרל משתרע לצד מסוים שלו, אז כאשר הצד של משטח האינטגרציה משתנה, אינטגרל פני השטח מהסוג השני משנה סימן להיפך- זהו ההבדל שלו מהאינטגרל של פני השטח מהסוג הראשון.

חישוב אינטגרלי פני השטח מהסוג השני מפחית לחישוב אינטגרלים כפולים.

תנו למשטח חלק S מכוון (בחרו את הצד העליון) להינתן במשוואה z = z (x, y), כאשר z (x, y) הוא רציף ב

שטח סגור S xy - הקרנה של פני השטח S על המישור xOy; הפונקציה f(x, y, z) רציפה על S. אז הנוסחה תקפה

∫∫ f(x, y, z) dxdy= ∫∫ f(x, y, z(x, y)) dxdy,
		S xy
מבטאים את אינטגרל פני השטח מהסוג השני על פני המשתנים x ו
דרך כפול. אם נבחר את הצד התחתון של המשטח S, אז מלפנים
אינטגרל, סימן מינוס יופיע בצד ימין.
הנוסחאות תקפות באופן דומה
∫∫ f(x, y, z) dydz= ∫∫ f(x(y, z), y, z) dydz,
		S yz
∫∫ f(x, y, z) dxdz= ∫∫ f(x, y(x, z), z) dxdz,
		S xz
שבו משטח S		לפי המשוואות	x = x(y, z)
y = y(x, z) ו-Syz	ו-S xz -	הקרנות של פני השטח S, בהתאמה

מטוסים yOz ו-xOz.

כדי לחשב את אינטגרל הצורה הכללי (4.6), נעשה שימוש בנוסחאות (4.7)-(4.9) אם פני השטח S מוקרן באופן ייחודי על כולם

לתאם מטוסים. במקרים מורכבים יותר, פני השטח S מחולק לחלקים בעלי התכונות המצוינות, והאינטגרל הכללי מוצג בצורת אינטגרלים על חלקים אלו.

דוגמה 4.2. חשב

∫∫ (y 2 + z 2 ) dxdy , כאשר S הוא הצד העליון

	משטח z =					1 - x 2			חתוך שטוח
	קוביות y = 0, y = 1.
					פִּתָרוֹן. המשוואה x 2 + z 2 = 1 -
	צוין גליל עגול עם גנרטריקס,
	מקביל לציר Oy, והמישור y = 0 ו
		y = 1			מַקְבִּיל				לְתַאֵם
	מטוס xOz (איור.									הַקרָנָה
	משטח S במישור xOy הוא
מלבן S xy המוגדר על ידי אי השוויון − 1 ≤ x ≤ 1,										0 ≤ y ≤ 1.
לאחר מכן, לפי הנוסחה (4.7) יש לנו
∫∫ (y2 + z2 ) dxdy= ∫∫ (y2 + (1 − x2 )) dxdy= ∫ dx∫ (y2 − x2 + 1) dy=
	S xy							−1
					+ (1- x 2 )y )
	= ∫ dx (
	−1

− x2 ) dx

= ∫ (

−1

−1

דוגמה 4.3. לחשב

∫∫ xdydz+ ydxdz+ zdxdy, כאשר S הוא העליון

צלע של חלק מהמישור x + z − 1 = 0

מנותק על ידי מישורים y = 0, y = 4 ו

ממוקם באוקטנט הראשון (איור 4.4).

פִּתָרוֹן. הקרנה של משטח S על

מישור xOy הוא המלבן S xy,

מוגדר על ידי אי השוויון 0 ≤ x ≤ 1,

0 ≤ y ≤ 4. הקרנה של משטח S על

מישור ה-yOz הוא מלבן

S yz, מוגדר על ידי אי השוויון

0 ≤ z ≤ 1,0 ≤ y ≤ 4. מכיוון שהמישור S מאונך למישור

xOz , then∫∫ ydxdz = 0. לאחר מכן, לפי נוסחאות (4.7) ו-(4.9) יש לנו

∫∫ xdydz+ ydxdz+ zdxdy= ∫∫ (1 − z) dydz+

S yz

+ ∫∫ (1 − x) dxdy= ∫ dy∫ (1 − z) dz+ ∫ dy∫ (1 − x) dx=

S xy

− z )

(1− x)

2 ∫

dy = 4.

= ∫ dy −

+ ∫ dy −

4.4. נוסחת אוסטרוגרדסקי. הנוסחה של אוסטרוגרדסקי קובעת קשר בין אינטגרל פני השטח על פני משטח סגור לבין האינטגרל המשולש על האזור המרחבי המוגבל על ידי משטח זה.

תנו ל-V להיות אזור סגור רגיל התחום על ידי פני השטח S, ותנו לפונקציות P(x, y, z), Q(x, y, z), R(x, y, z)

הם רציפים יחד עם הנגזרות החלקיות מהסדר הראשון שלהם באזור נתון. אז הנוסחה הבאה מתקיימת:

∫∫∫(	∂P		∂ ש		∂ R ) dxdydz= ∫∫ Pdydz+ Qdxdz+ Rdxdy, (4.10)
	∂x		∂י		∂z

שקוראים לוהנוסחה של אוסטרוגרדסקי 1 .

באמצעות הנוסחה של אוסטרוגרדסקי נוח לחשב אינטגרלי משטח על פני משטחים סגורים.

דוגמה 4.4.באמצעות הנוסחה של אוסטרוגרדסקי, חשב

∫∫ xdydz + ydxdz + zdxdy ,

איפה ס

הצד של הפירמידה

מוגבל

מטוסים

איקס + y + ז = 1,

איקס= 0,y= 0,

ז= 0 (איור 4.5).

לפי

אוסטרוגרדסקי:

פ(איקס,y,ז)= איקס,ש(איקס,y,ז)= y,ר(איקס,y,ז)= ז.

לאחר מכן: ∂ פ+

∂ ש+

∂ר

= 1+ 1+ 1= 3,ואנחנו מוצאים

∂איקס

∂y

∂ז

1− איקס

1 −איקס−y

∫∫ xdydz + ydxdz + zdxdy = 3 ∫∫∫ dxdydz = 3 ∫ dx ∫ dy

∫ dz =

1− איקס

1 −איקס−y

1− איקס

= 3 ∫ dx ∫ dy ∫ dz = 3 ∫ dx ∫ (1 − איקס − y ) dy =

y 2

1− איקס

3 ∫ dx ( y − xy −

−2 איקס+1

3 (איקס− 1)

= 3 ∫ (1 −איקס−איקס+איקס2 −

) dx =

∫ (איקס − 1) 2 dx =

הערה 4.1.הקשר בין אינטגרלים משטחים מהסוג הראשון והשני דומה לחיבור בין אינטגרלים עקומים:

∫∫ ו (איקס , y , ז ) dxdy = ∫∫ ו (איקס , y , ז )חַסַת עָלִיםα ds ,

∫∫ ו (איקס , y , ז ) dydz = ∫∫ ו (איקס , y , ז )חַסַת עָלִיםβ ds ,

∫∫ ו (איקס , y , ז ) dxdz = ∫∫ ו (איקס , y , ז )חַסַת עָלִיםγ ds ,

איפה חַסַת עָלִיםα ,חַסַת עָלִיםβ ,חַסַת עָלִיםγ - קוסינוס כיוון של הנורמלי המקביל ל

הצד הנבחר של פני השטח. ,y)

רציף באזור סxy– הקרנות פני השטח ס

למטוס xOy;ל

- קווי המתאר,

מגביל

משטח

ס ; ל –

הקרנת קו החלל ללמטוס

xOy ,

להיות

מלונה המגבילה את השטח ד. בוא נבחר את הצד העליון

משטחים ס. אם הפונקציות פ(איקס, y, ז), ש(איקס, y, ז), ר(איקס, y, ז)

רָצִיף

יחד עם נגזרותיו החלקיות מסדר ראשון על

משטחים ס, אז מתקיימת הנוסחה הבאה:

∫ Pdx + Qdy + Rdz =

= ∫∫

(∂ ש

∂ פ) dxdy + (

∂ר

∂ ש) dydz + (∂ פ

∂ ר) dxdz

∂איקס

∂y

∂y

∂ז

∂ז

∂איקס

(ל- נע בכיוון חיובי)

שקוראים לו נוּסחָה

אם כמשטח סלקחת שטח דעל פני השטח xOy

(ז= 0 ), ואז מ-(4.11) נקבל את הנוסחה של גרין

∂ש

∂ פ) dxdy .

∫ פ (איקס , y ) dx + ש (איקס , y ) dy = ∫∫ (

∂איקס

∂y

לפיכך, הנוסחה של גרין היא מקרה מיוחד של הנוסחה של סטוקס.

שימו לב שאינטגרל פני השטח מהסוג השני בנוסחה

ניתן להחליף סטוקס (4.11) באינטגרל פני השטח של הראשון

סוּג. אז הנוסחה הזו תקבל את הצורה

∫ Pdx + Qdy + Rdz =

∂ש

∂פ

∂ר

∂ש

∂פ

∂ר

= ∫∫

)חַסַת עָלִים α + (

)חַסַת עָלִים β + (

)חַסַת עָלִים γ

∂איקס

∂y

∂y

∂ז

∂ז

∂איקס

ds ,

איפהחַסַת עָלִים α ,חַסַת עָלִים β ,חַסַת עָלִים γ ,

מתכוון

מדריכים

קוסינוסים

המתאים לצד הנבחר של המשטח.

באמצעות הנוסחה

לחשב

∫ איקס 2 y 3 dx + dy + zdz ,

מעגל,

נתון על ידי המשוואות

איקס 2 + y 2 + 1, ז = 0 .

משטח סהצד העליון של חצי הכדור משרת

איקס 2+ y 2+ ז 2= 1,

ז> 0 (להולך לכיוון חיובי).

למקרים שבהם האינטגרציה מתרחשת לא על קטע של עקומה, אלא על פני משטח מוגבל. כמו אינטגרלים עקומים, אינטגרלים משטחים הם מהסוג הראשון ומהסוג השני.

אינטגרל משטח מהסוג הראשון כתוב בצורה

איפה ו(M) = ו(x,y,z) הוא פונקציה של שלושה משתנים, והמשטח σ - אזור שילוב של פונקציה זו. אם ו(x,y,z) שווה לאחדות, ואז אינטגרל פני השטח שווה לשטח הפנים.

דמיינו לעצמכם חמנייה גדולה למדי עם זרעים מאוד מאוד קטנים. לאחר מכן, מסכום המשטחים של זרעים מאוד מאוד קטנים הממוקמים על פני החמנייה, אפשר לחשב את פני החמנייה - זו עשויה להיות פרשנות פשוטה של ​​אינטגרל פני השטח. למה?

הבה נעבור להגדרה רשמית יותר של אינטגרל משטח. משטח σ מחולק ל נחלקים עם שטחים Δ σ 1 , Δ σ 2 , ..., Δ σ נ. אם תבחר נקודה שרירותית על כל משטח חלקי (זרע) Mאניעם קואורדינטות ( ζ אני, η אני, ς אני ,), אז נוכל לסכם

סכום זה נקרא הסכום האינטגרלי של הפונקציה ו(M) על פני השטח σ . כעת נמקסם את המספר של חלקים קטנים כאלה, ואת הקוטר הגדול ביותר Δ σ אני- להיפך, להפחית. אם לסכום האינטגרלי כגדול בקטרים ​​של החלקים שואף לאפס (כלומר, כפי שכבר ציינו, כל החלקים קטנים מאוד) יש גבול, אז הגבול הזה נקרא אינטגרל משטח מהסוג הראשון מהפונקציה ו(M) על פני השטח σ .

חישוב אינטגרל פני השטח מהסוג הראשון

תן למשטח σ נתון על ידי המשוואה ז = ז(איקס, y) , ההקרנה שלו על המטוס xOyהוא האזור דxy, תוך כדי הפונקציה ז = ז(איקס, y) ונגזרותיו החלקיות הן רציפות באזור דxy.

דוגמה 1.

איפה σ - חלק מהמטוס באוקטנט הראשון.

פִּתָרוֹן. צִיוּר:

ממשוואת המישור נקבל את הביטוי "זט": .

אז הנגזרות החלקיות הן: , ו

.

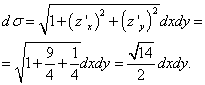משטח σ הוא המשולש המוצג בציור א ב ג, והקרנתו על המטוס xOy- משולש AOB, אשר מוגבל בקווים ישרים איקס = 0 , y= 0 ו-3 איקס + y= 6. בואו נעבור מהאינטגרל של פני השטח לאינטגרל הכפול ונפתור אותו:

.

הרעיון של אינטגרל משטח מהסוג השני

לפני המעבר להגדרה של אינטגרל משטח מהסוג השני, יש צורך להכיר את המושגים של צלעות של משטחים ומשטחים מכוונים.

תן משטח חלק להינתן בחלל σ . בואו נבחר נקודה שרירותית על פני השטח הזה Mוצייר את הווקטור הנורמלי אל פני השטח דרכו. דרך הנקודה Mנבצע גם על פני השטח σ קו מתאר שרירותי שאין לו נקודות משותפות עם גבול פני השטח σ . עצירה מוחלטת Mיחד עם הווקטור הנורמלי, ננוע לאורך קו המתאר כך שהווקטור הנורמלי יהיה כל הזמן מאונך למשטח σ . עם החזרת הנקודה Mלמיקום ההתחלתי, שני מקרים אפשריים: כיוון הווקטור הנורמלי יישאר זהה או ישתנה להיפך.

אם כיוון הווקטור הנורמלי אינו משתנה, אז פני השטח σ נקרא דו צדדי. אם, כאשר חוצים את קווי המתאר, כיוון הווקטור הנורמלי משתנה להפך, אז המשטח נקרא חד צדדי. משטחים דו-צדדיים נקראים משטחים מכוונים, משטחים חד-צדדיים נקראים משטחים לא מכוונים.

דוגמה למשטח חד צדדי הוא רצועת מוביוס (בתמונה למעלה), שניתן להכין מרצועת נייר שצד אחד מסובב 180 מעלות ואז הקצוות מודבקים זה לזה. והנה מה שחשוב כאן: עבור משטח חד צדדי המושג של אינטגרל משטח מהסוג השני אינו מוצג .

אז נשקול רק משטחים דו-צדדיים. דוגמאות למשטחים דו-צדדיים הם מישורים, כדורים, אליפסואידים ופרבולואידים.

הצד החיובי של משטח דו-צדדי קובע את כיוון הווקטור הנורמלי. הצד הנגדי של פני השטח נקרא שלילי. הצד החיובי של משטח הוא הצד העליון שלו. אם היחידה וקטורים נורמליים יוצרים זוויות חדות עם הציר עוז, ואז הצד העליון של המשטח נבחר ז = ז(איקס, y) , אם הזוויות קהות, אז הצד התחתון של המשטח.

כמו במקרה של אינטגרל פני השטח מהסוג הראשון, ניתן לחלק את המשטח ל נחלקים. בעת ניסוח המושג אינטגרל פני השטח מהסוג הראשון, הסכום האינטגרלי כלל את השטחים של כל אחד מהחלקים שבהם הוכפלו ערכי הפונקציה ו(Mאני). במקרה של אינטגרל משטח מהסוג השני, שטחי החלקים עצמם אינם נלקחים, אלא אזורי ההקרנות שלהם על מישורי קואורדינטות . וכדי להבחין בין הפונקציה של שלושה משתנים לאינטגרל מהסוג הראשון שאנו מציינים ר(איקס,y,ז) . אז הסכום האינטגרלי ייכתב באופן הבא:

,

שבו Δ סאני- השטחים של ההקרנות שהוזכרו של חלקי צד המשטח על ציר הקואורדינטות (לעת עתה נניח שעל הציר xOy).

עם מוסכמות וסימון כאלה, ההגדרה של אינטגרל משטח מהסוג השני דומה להגדרה של אינטגרל מהסוג הראשון. כלומר: אינטגרל משטח מהסוג השני הוא הגבול של סכום אינטגרלי נתון שכן הקוטר הגדול ביותר של חלקי המשטח הנבדק שואף לאפס.

זה כתוב כך:

.

במקרה זה הפונקציה ר(איקס,y,ז) אינטגרלי על משתנים איקסו y, שכן חלקים מהמשטח הוקרנו על המטוס xOy.

באופן דומה, אנו יכולים לכתוב שני אינטגרלים משטחים אחרים מהסוג השני:

(פוּנקצִיָה פ(איקס,y,ז) אינטגרלי על משתנים yו ז yOz),

(פוּנקצִיָה ש(איקס,y,ז) אינטגרלי על משתנים זו איקס, שכן חלקים מהמשטח מוקרנים על המטוס zOx).

סכום האינטגרלים הללו

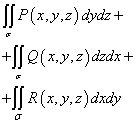
שקוראים לו אינטגרל משטח כללי מהסוג השני והוא מיועד

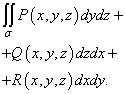
חישוב אינטגרל פני השטח מהסוג השני

אינטגרל משטחי מהסוג השני מחושב על ידי פירוק האינטגרל המשטחי הכללי של הסוג השני לסכום אינטגרלי משטח (ראה סוף הפסקה הקודמת) והפחתת כל אחד מהם לאינטגרל כפול.

הבה נבחן בפירוט את חישוב האינטגרל

.

תן למשטח σ נתון על ידי המשוואה ז = ז(איקס, y) . אנו מציינים את הצד החיובי של פני השטח, את הצד השלילי ואת ההקרנה על המישור xOy - דxy.

לפיכך, אנו מקבלים נוסחה לחישוב אינטגרל פני השטח מהסוג השני:

אם הצד השלילי של פני השטח נבחר, סימן האינטגרל משתנה:

שני האינטגרלים הנפרדים האחרים - מונחי האינטגרל הכללי - מחושבים באופן דומה:

דוגמה 2.

,

איפה σ - הצד העליון של חלק מהמטוס, מנותק על ידי מטוסים y= 0 ו y= 4 וממוקם באוקטנט הראשון.

פִּתָרוֹן. הציור נמצא בתמונה למעלה. בהגדרה, אנו מקבלים את הסכום של שלושה אינטגרלים כפולים:

האינטגרל השני שווה לאפס, מאז המישור σ מקביל לציר אוי. לכן, אנו מוצאים את האינטגרל הראשון והשלישי:

כל שנותר הוא לחבר את כל האינטגרלים האינדיבידואליים ולהשיג את אינטגרל פני השטח הכללי מהסוג השני:

.

אם אתה צריך לחשב אינטגרל משטח מהסוג השני על פני משטח סגור, אתה יכול ללכת ל אינטגרל משולש, באמצעות נוסחת אוסטרוגרדסקי. לאחר מכן, אם הפונקציות פ(x,y,z) , ש(x,y,z) ו ר(x,y,z) והנגזרות החלקיות שלהם , , הן פונקציות רציפות בתחום W, אשר תחום על ידי משטח סגור σ , ואז כאשר משתלבים על החלק החיצוני של פני השטח, השוויון

דוגמה 3.חשב אינטגרל משטח מהסוג השני

,

איפה σ - הצד החיצוני של פני השטח של חרוט שנוצר על ידי משטח ומישור ז = 2 .

פִּתָרוֹן. משטח זה הוא פני השטח של חרוט בעל רדיוס ר= 2 וגובה ח= 2 . זהו משטח סגור, כך שניתן להשתמש בנוסחה של אוסטרוגרדסקי. כי פ = 3איקס , ש = 4y , ר = −ז, ואז הנגזרות החלקיות , , .

נעבור לאינטגרל המשולש, אותו אנו פותרים:

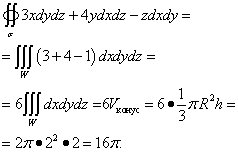
דוגמאות נוספות לחישוב אינטגרלי משטח

דוגמה 4.חשב אינטגרל משטח מהסוג הראשון

איפה σ - משטח לרוחב של החרוט ב .

פִּתָרוֹן. מאז הנגזרות החלקיות , , זה

אנו מצמצמים אינטגרל משטח זה לכפול:

הקרנה של משטח על מישור xOyהוא עיגול עם מרכז במקור וברדיוס ר= 2, לכן, בחישוב האינטגרל הכפול, נעבור למערכת הקואורדינטות הקוטבית. לשם כך, בואו נשנה את המשתנים:

אנו משיגים את האינטגרל הבא, אותו אנו פותרים לבסוף:

דוגמה 5.חשב אינטגרל משטח מהסוג השני

,

איפה σ - חלקו העליון של המשולש הנוצר בהצטלבות המישור עם מישורי הקואורדינטות.

פִּתָרוֹן. הבה נחלק את האינטגרל המשטח הזה בסכום של שני אינטגרלים

, איפה

.

כדי לחשב את האינטגרל אני1 σ למטוס yOz. ההקרנה היא משולש OCB, שנמצא במטוס yOzלהגביל קווים ישרים או, y= 0 ו ז= 0 . ממשוואת המישור נגזרת. לכן נוכל לחשב את האינטגרל אני1 :

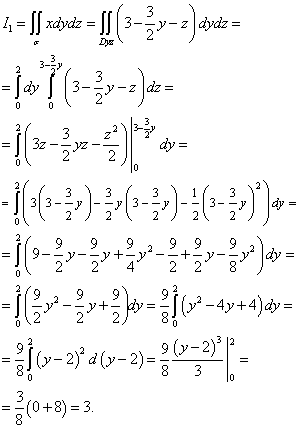
כדי לחשב את האינטגרל אני2 , בואו נבנה הקרנה משטחית σ למטוס zOx. ההקרנה היא משולש AOC, אשר תחום בקווים ישרים או , איקס= 0 ו ז= 0 . אנו מחשבים:

אנו מוסיפים את שני האינטגרלים המתקבלים ולבסוף מקבלים את אינטגרל השטח הזה:

.

דוגמה 6.חשב אינטגרל משטח מהסוג השני

,

איפה σ - המשטח החיצוני של פירמידה שנוצר על ידי מישור ולתאם מטוסים.

דוגמה 3.3.חשב את העבודה של שדה וקטור

א = 2איקס 2 y אני – xy 2 י

מהמקור O לנקודה A(1;1), אם התנועה מתרחשת לאורך: א)קטע קו; ב)קשתות של פרבולה; V)קו שבור OBA, שבו B(1;0) (ראה איור 3.1).

פִּתָרוֹן . א)למשוואת הישר OA יש את הצורה y=x. לתת x=t, אז המשוואה של הישר בצורה פרמטרית תקבל את הצורה:

x=t, y=t,

וכשעוברים מ-A ל-B הפרמטר טישתנה מ-0 ל-1. אז העבודה שנעשתה תהיה שווה ל

ב)לתת x=t 2 , y=t, לאחר מכן

x=t 2 , y=t, 0£ ט£1 .

.

V)משוואת הישר (OB) היא y=0 (0£ איקס£1); למשוואת הישר (BA) יש את הצורה איקס=1 (0 £ y£1). לאחר מכן

, .

כתוצאה מכך, אנו מקבלים,

.

תגובה. אם במקרה של שדות דו מימדיים משוואת הקו מתוארת על ידי המשוואה y=y(איקס), והמשתנה x משתנה מ אלפני ב, אז האינטגרל העקמומי של ה-2 יחושב על ידי הנוסחה:

. (3.9)

ניתן לפתור את הדוגמה הקודמת באמצעות נוסחה זו מבלי להציג את הפרמטר ט.

דוגמה 3.4.חשב אינטגרל

,

כאשר L היא הקשת של הפרבולה y=x 2 +1 מנקודה A(0;1) לנקודה B(2;5).

פִּתָרוֹן . בואו נעשה ציור (ראה איור 3.2). ממשוואת הפרבולות נקבל y"=2x. מאז על קשת פרבולה א.במִשְׁתַנֶה איקסמשתנה מ-0 ל-2, ואז האינטגרל העקמומי, בהתאם לנוסחה (3.9), יקבל את הצורה

4. אינטגרלי פני השטח

4.1. אינטגרלי משטח מהסוג הראשון

אינטגרל פני השטח מהסוג הראשון הוא הכללה של האינטגרל הכפול ומוצג באופן דומה. שקול קצת משטח ס, חלק או חלק חלק, והנח שהפונקציה f( x,y,z) מוגדר ומוגבל על משטח זה. הבה נחלק את המשטח הזה ל נחלקים שרירותיים. השטח של כל חלקה מסומן על ידי ד אני. בכל קטע נבחר נקודה עם קואורדינטות ( x i, y i, z i) וחשב את ערך הפונקציה בכל נקודה כזו. לאחר מכן, אנו יוצרים את הסכום האינטגרלי:

.

אם יש מגבלה של סכומים אינטגרליים ב נ®¥ (במקרה זה מקסימום D אני®0), כלומר. מגבלה כזו אינה תלויה לא בשיטת החלוקה או בבחירת נקודות האמצע, ואז מגבלה כזו נקראת אינטגרל משטח מהסוג הראשון :

. (4.1)

אם הפונקציה f( x,y,z) הוא רציף על פני השטח ס, אז הגבלה (4.1) קיימת.

אם הפונקציה האינטגרנד f( x,y,z)º1, אז אינטגרל פני השטח מהסוג הראשון שווה לשטח הפנים ס:

. (4.2)

הבה נניח שמוצגת מערכת קואורדינטות קרטזית, וכל ישר מקביל לציר עוז,יכול לחצות את פני השטח סרק בשלב אחד. ואז משוואת פני השטח סניתן לכתוב בטופס

z = z(x,y)

והוא מוקרן באופן ייחודי על המטוס xOy. כתוצאה מכך, ניתן לבטא את אינטגרל פני השטח מהסוג הראשון במונחים של האינטגרל הכפול

. (4.3)

דוגמה 4.1.חשב אינטגרל

,

איפה ס– חלק מהמשטח החרוטי ז 2 =איקס 2 +y£2.0 ז£1.

פִּתָרוֹן. יש לנו

ואז האינטגרל הנדרש הופך לאינטגרל כפול

איפה S xy- מעגל איקס 2 +y 2 פאונד 1. בגלל זה

.

4.2. אינטגרלי משטח מהסוג השני

אפשר לציין שדה וקטור באזור כלשהו

א = a x אני + א y י + א ז ק

וכל משטח דו צדדי ס. הבה נחלק את פני השטח בצורה כלשהי לאזורים יסודיים D S i. בכל אתר אנו בוחרים נקודה שרירותית P אניוהרכב את הסכום האינטגרלי:

, (4.4)

איפה נ (פאי) – וקטור נורמלי למשטח נתון בנקודה פאי. אם יש הגבלה לסכום כזה לפי ד S i®0, אז הגבול הזה נקרא אינטגרל משטח מהסוג השני (אוֹ זְרִימָה שדה וקטור א דרך פני השטח ס) ומסומן בסמל

או ,

איפה ד ס =נ ds.

מאז היחידה הרגילה יש קוסינוס כיווני בתור הקואורדינטות שלו נ =(cosa, cosb, cosg). זֶה

לפיכך, ניתן לצמצם את חישוב אינטגרלי פני השטח מהסוג השני לחישוב אינטגרלי פני השטח מהסוג הראשון. אולם, מה בניגוד לאינטגרלי משטח מהסוג הראשון, אינטגרלים מהסוג השני תלויים בבחירת צד המשטח. מעבר לצד השני של המשטח משנה את כיוון הנורמלי אל פני השטח, ובהתאם, את סימן האינטגרל.

קחו בחשבון את האינטגרל

.

תן למשוואת פני השטח את הצורה ז=j( x,y) והצד החיובי של משטח זה ייחשב לזה שהצורה הרגילה שלו נוצרת עם ציר O זפינה חדה. לאחר מכן

cosg ds = dxdy.

לכן, ניתן לכתוב את האינטגרל הנדון בטופס

.

מחליף זמאת j( x,y), אנו מגיעים לאינטגרל הכפול

,

איפה S xy- הקרנת משטח סלמטוס xOy.